[논문리뷰] Skyline Queries: an Introduction (skyline query란?)

논문 정보
제목	Skyline Queries: an Introduction
저자	Eleftherios Tiakas, Apostolos N. Papadopoulos, Yannis Manolopoulos
소속	Department of Informatics Aristotle University 54124 Thessaloniki, Greece
저널	IEEE
DOI	10.1109/IISA.2015.7388053
주제	Information, Intelligence, Systems and Applications (IISA)
논문제출일	2016.01
인용수	36회 (2025.02.12 기준)

 

이번에 대학원에서 프로젝트 관련해서

공간데이터로 할 수 있는 query에 대해 찾아보다가

skyline query라는 것을 찾아서

위 논문의 내용을 바탕으로 해서 정리해보고자한다

---

Skyline Query의 정의

skyline query는 다중 기준 의사 결정을 도와주는

알고리즘이라고 할 수 있다

 

예를 들면

"경복궁과 가까운 호텔을 추천해줘"라는 질문이 들어온다면

어떤 호텔을 갈지 결정하는 기준에는

경복궁과의 거리, 평점, 가격 등이 있을 수 있다

 

이렇게 거리, 평점, 가격과 같이 다중 기준을 고려해서

어떤 호텔을 갈지 의사결정을 해야하는데

이런걸 해결해주는 알고리즘이다

 

이런 skyline query와 알고리즘은

2016년 기준 이전에도 수십년동안 데이터베이스 커뮤니티에서도

큰 주목을 받았고 활발하게 연구가 되어왔다고한다

 

그렇다면 대충 skyline query가 어떤 것인지 알았으니

이제 skyline query가 어떤 객체를 반환해야하는지 알아보자

 

논문의 정의에 따르면,

데이터셋에서 지배관계가 주어졌을 때 skyline query는

다른 객체들에 의해 지배될 수 없는 객체들을 반환한다.

다차원 객체로 구성된 데이터셋의 경우

객체는 모든 차원에서 동일하거나 더 우수하고

최소한 하나의 차원에서 더 우수한 경우에 다른 객체를 

 

이게 무슨말인가..하면

위 경복궁과 가까운 호텔 추천 예시로 한 번 살펴보자

거리, 평점, 가격을 1부터 100까지의 점수체계로 정규화를 했다고 하자

그리고 점수가 높을수록 좋은 것이라고 가정하자

 

각 기준들을 skyline query에서는 차원이라고 한다

어떤 객체에거리, 평점, 가격이라는 기준이 있으면

3차원 객체가 되는 것이다

 

A호텔은 (거리, 평점, 가격)이 각각 (90, 100, 100)이고

B호텔은 (거리, 평점, 가격)이 각각 (50, 50, 50)이라고 하자

 

그럼 모든 차원에서 A호텔은 B호텔보다 좋다

그 어떤 경우에서도 A호텔을 내버려두고 절대 B호텔을 선택할 수가 없다

이런 경우를

"A호텔이 B호텔을 지배한다"라고 말한다

이렇게되면 B호텔은 skyline 후보에서 탈락하게되고

A호텔은 skyline 후보가 되게된다

 

그런데 C호텔은 점수가 (100, 80, 100)이라고 하자

이렇게 되면 C호텔은 A호텔에 비해 거리에선 좋지만

평점에서는 좋지 못하게 된다

이런 경우 C호텔을 버리고 무조건 A호텔을 선택할수도

A호텔을 버리고 무조건 C호텔을 선택할수도 없게된다

 

이런 경우는 "C호텔은 A호텔에게 지배되지않는다"라 말하고

C호텔도 skyline 후보인 A호텔에게 지배되지 않았기때문에

skyline 후보가 되게된다

 

이런식으로 계속해서 반복해서

최종적으로 모든 객체에게도 지배되지않는 객체들의 집합이

skyline query의 반환값이 되는 것이다

 

2차원 데이터에서 그래프로 예시를 보면 이해가 쉽다

 

위 그래프의 경우 skyline query의 반환값은

a, b, e, h, o가 된다

(각 차원마다 점수가 낮을수록 좋은 것이라고 가정했을때)

 

a, b, e, h, o 이외에 다른 객체들은

모두 a, b, e, h, o에 의해서 지배된다는 것을 알 수 있다

 

 

 

Algorithm 종류

skyline query를 naive하게 하려면

각각의 객체를 다 비교해야하고 이렇게 되면

시간복잡도는 O(n제곱)이 된다

 

이에 따라 skyline query를 좀 더 빠르고 효율적으로

수행하기 위해 다양한 연구들이 진행되었다

효율적으로 skyline query를 해결하는 알고리즘의 종류를

index와 비-index기반으로 구분해서 알아보자

 

Non-Index-Based Algorithms

Block-Nested-Loop(BNL)

 

BNL 알고리즘은 naive한 skyline query와

동일한 아이디어를 가져가지만

window를 사용하여 저장할 데이터수의 객체를 제한한다

 

window 내부에서 어떤 객체 p가

다른 객체들에의해 지배되는지 검사하는 과정을 거친다

 

그러다가 window가 가득차면

후보 객체들은 임시 디스크 파일에 저장된다

 

BNL 알고리즘은 크기가 작은 데이터셋에 잘 작동하며

최악의 경우는 naive skyline query 알고리즘과 같이

O(n제곱)이지만 실제로 훨씬 더 나은 I/O 성능을 보인다고한다

 

이러한 BNL을 조금 변형하여

객체 지배부분에 관하여 위상정렬을 통해

조금 더 효율적으로 만든 알고리즘이

SFS 알고리즘이고,

SFS 알고리즘의 확장판이 SaLSa 알고리즘이다

 

 

Divide and Conquer (DC)

알고리즘 기법 중 분할정복기법(Divide and Conquer)을

skyline query에 적용한 것이다

 

하나의 차원에서 중앙값을 계산하고

그 기준으로 파티션을 P1, P2로 나눈다

그다음 각 파티션을 또 재귀적으로 나누다가

객체가 하나만 남을 때 종료된다

 

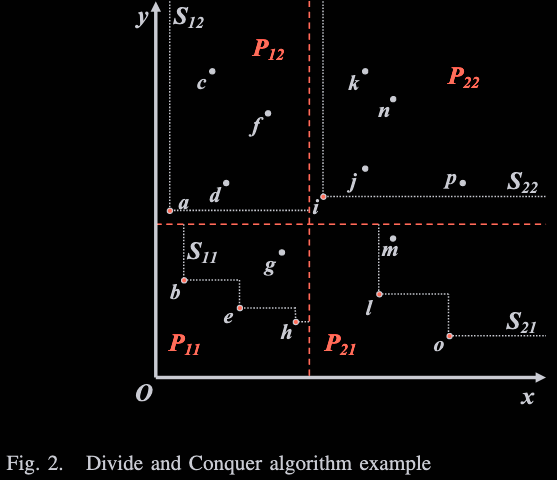
위는 DC를 이용한 skyline query의 예시이다

처음에는 P1과 P2로 분할된 뒤

그 안에서 또 각각 S1과 S2로 분할된다

 

이렇게 됐을 때

S12에서는 skyline 후보가 a

S11에서는 b, e, h

S22에서는 i

S21에서는 i, o가 되는데

 

여기서 S11의 점들은 무조건 skyline이 되며

S22의 점들은 S11에게 무조건 지배당하기 때문에

skyline 후보에서 탈락하게된다

 

그다음 S12는 S11과 비교해서 a가 살아남고

S21도 S11과 비교해서 o만 살아남게된다

 

따라서 최종 skyline으로 반환되는 객체는

a, b, e, h, o가 되는 것이다

 

최악의 경우 시간복잡도는

O(N (log N )(d−2)) + O(N log N )가 된다고한다

 

 

 

Bitmap

비트맵 인코딩을 기반으로 한 알고리즘이 제안되었다

각 객체는 m비트 벡터로 매핑되며

m은 d차원에서의 고유값의 총합이다

 

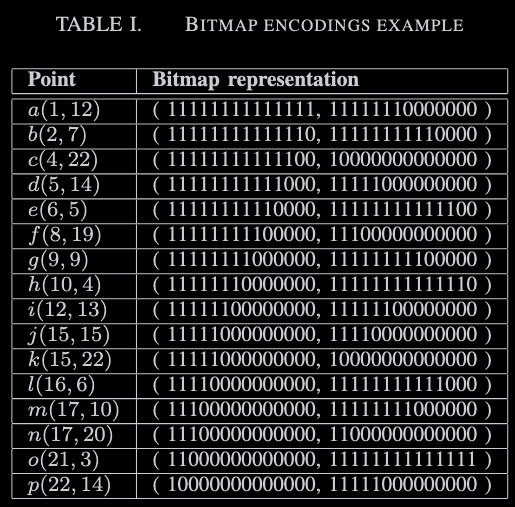
위는 bitmap encoding의 예시이다

위예시를 보면 각 x, y차원은 14자리의 비트맵으로 구성되어있고

m=28이 된다

 

bitmap encoding으로 점(x, y)가 skyline인지 알려면

x와 y차원에 해당하는 오른쪽 가장자리 비트들을 이어붙인 것중에

1이 한개만 있는지 확인하면 된다

 

예를 들어 점 h(10, 4)에 대해

x-인코딩에서 8번째 오른쪽 비트와 y-인코딩에서 2번째 오른쪽 비트를 취하면

sx=1111111100000000, sy=0000000100000010이고 이를 합치면

sx&sy=0000000100000000이 된다

이 결과는 점 h가 스카이라인에 포함된다는 것을 의미한다

 

하지만 g(9, 9)은 x-인코딩에서 7번째 오른쪽 비트와

y-인코딩에서 6번째 오른쪽 비트를 취해서

sx=1111111000000000, sy=0100101100010010이 되고

sx&sy=0100101000000000이 되기 때문에

점 g는 skyline에 포함되지 않는다

 

 

Index-based Algorithm

이제 인덱싱 기법을 활용하는

skyline query들을 알아보자

 

B-Tree

B-Tree를 이용한 skyline query는

각 차원에서 정렬된 인덱스를 사용한다

 

 

위는 각 점들을 x와 y차원에서 정렬한 것이다

 

이 2개의 인덱스를 동시에 스캔하여

어떤 점 p가 두개의 인덱스에서 발견된다면

스캔을 그만한다

 

위 예시를 보면

x와 y 인덱스값을 각각 Round Robin 방식으로 스캔한다

그렇게되면 y에서 e가 스캔되고 계속해서 스캔하다가

x에서 e가 스캔되었기 때문에

x와 y 각 차원에서 모두 e가 발견되었기 때문에 스캔을 종료한다

 

이렇게 된다면 e이후에 있는 객체들은

모두 e에 의해 지배된다고 판단하여 스캔할 필요가 없어진다

 

이제 그렇게 된 후 e전에 스캔했던

a, b, c, d, l, o, h 중 지배 관계를 확인한다

a가 c, d를 지배하고 h는 l을 지배한다

따라서 지배되는 것을 제거하면

최종 스카이라인 객체는

a, b, e, h, o가 된다

 

 

 

R-Trees

R-Tree를 이용한 skyline 객체 추출법이다

 

1. 최근접 이웃 검색(Nearest Neighbor Search)

NN알고리즘이라고도 불리는 최근접 이웃검색 알고리즘은

유클리드 거리를 기반으로 반복적으로

최근접 객체를 찾아가는 알고리즘이다

 

따라서 원점에 대해서 최근접객체를 찾고

해당 객체가 공간 전체를 지배하면 나머지를 버리고

지배하지 못하는 영역은 다시 분할해서

동일한 알고리즘을 수행한다

 

아래 예시를 통해 이해해보자

 

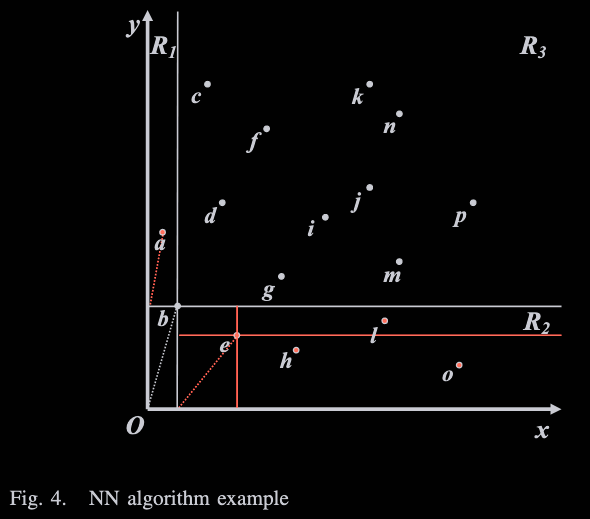
가장 처음에 유클리드거리 계산을 통해

원점과 가장 가까운 객체 b를 찾아냈다

그럼 b를 기준으로 x와 y모두 b보다 큰 영역은

b에 의해 지배당하므로 R3영역은 버린다

 

그런 다음 지배당하지 않는 영역을

R1과 R2로 나눈 다음

각 영역에서의 원점과 가장 가까운 객체를 찾는다

R1은 a가 되고, R2는 e가 된다

 

R1에서는 객체가 a뿐이므로 a는 skyline이 되고

R2에서는 l은 e에 의해 지배당하므로 제거된다

 

이러한 과정을 반복해서 결국 skyline 객체는

a, b, e, h, o가 반환된다

 

 

2. Branch and Bound Skyline algorithm (BBS)

BBS도 NN을 기반으로 하는 알고리즘이며

R-Tree 구조로 인덱싱을 하고

거리는 맨해튼거리(L1)를 사용한다

 

 

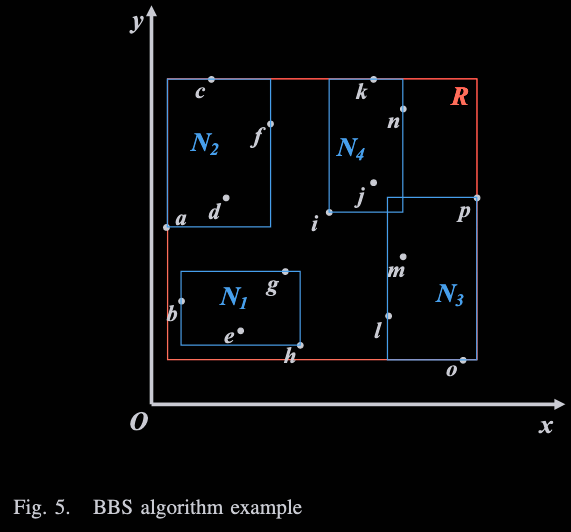
위 예시를 통해서 알고리즘을 살펴보자

 

우선 노드용량이 4인 R-Tree를 구성한다

R-Tree indexing 과정을 통해

N1, N2, N3, N4와 같은 구조로 인덱싱이 되었다

위 그래프에서 각 사각형을

최소 경계 사각형(Minimum Bound Rectangle, MBR)이라고 한다

최소 경계 사각형에서 원점과 최소거리는

좌측 하단 모서리의 좌표 합이다

 

위 R-Tree에서는 root node는 R이고

그 자식들로 N1, N2, N3, N4가 있는 것인데

R에서 시작하여 자식들의 최소 거리를 계산하여

Heap에 넣어준다

 

그럼 Heap H는

H={(N1,6),(N2,13),(N3,19),(N4,25)}이 되고

N1이 Heap에서 최상위객체가 되므로

N1객체를 풀어서 각 객체들의 최소 거리와 함께

다시 Heap에 정렬한다

 

그럼

H={(b,9),(e,11),(N2,13),(h,14),(g,18),(N3,19),(N4,25)}

이 된다

 

그럼 b 객체는 위 heap에서 최상위객체가 되므로

b는 skyline 후보가 되고

heap에서 b를 제거한다

 

그런 다음 위 heap에서 b에 의해 지배되는 것을 제거하고

또 다시 최상위객체를 뽑아 skyline 후보로 넣는다

 

이런 과정을 반복해서 결국 최종 skyline으로 뽑히는 것은

a, b, e, h, o가 된다고 한다

---

이 이후에 부분공간과 제약이 있는 skyline query,

분산 및 병렬 skyline query,

동적 환경에서의 skyline query에 대해서도

논문에서는 간단하게 언급하고있다

 

 

skyline query라는 개념을

공간 skyline query에서 처음 접해봤는데

이런 개념이 있다는 것도 신기했고

처음에는 추천 알고리즘과 비슷하다고는 생각했다

 

결국 다양한 기준을 적절히 고려해서

상위권의 객체를 추출하는일이라

추천 알고리즘과 비슷하다고 생각했는데

계속 생각해보니 기본 원리같은 측면에서

확연하게 다르다는 생각이 들었다

 

우선 가장 다르다고 생각했던 것은

요즘 수행되는 추천은 모두 ML/DL 기반이고

이 근간이 되는 것은 바로 '유사도'이다

하지만 skyline query는 객체들간의

유사도를 계산해서 가장 좋은 객체를

확률적 계산을 통해 정답을 내놓는다기보다는,

"절대 지배 당하지 않는 객체"라는 확실한 정답이 있고

이를 알고리즘으로 찾아가는 것이라는 생각이 들었다

 

아무튼 이 논문은 2015년 논문이라

최신 논문들을 보면서

요즘은 어디까지 해당 알고리즘이 발전을 했고

어떤 방향으로 연구가 진행되고있는지 보면 좋을 것 같다

 

또한 내 전공인 spatial data 부분에서

skyline query가 어떻게 활용되고있는지도

계속해서 볼 필요가 있을 것 같다