본 게시글은 Stanford 대학교 Jure Leskovec 교수님의
Stanford CS224W: Machine Learning with Graphs(2021) 강의를 듣고
학습을 목적으로 재구성한 글입니다
스스로 정리한 내용이라 오류가 있을 수 있습니다
https://web.stanford.edu/class/cs224w/
CS224W | Home
Content What is this course about? Complex data can be represented as a graph of relationships between objects. Such networks are a fundamental tool for modeling social, technological, and biological systems. This course focuses on the computational, algor
web.stanford.edu
https://www.youtube.com/watch?v=6g9vtxUmfwM&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=15
이제부터 본격적으로 Graph Neural Network에 대한 내용으로 들어간다
위 내용에 들어가기에 앞서 지난 시간에 배운 내용을
간단하게 살펴보고 넘어가려고 한다
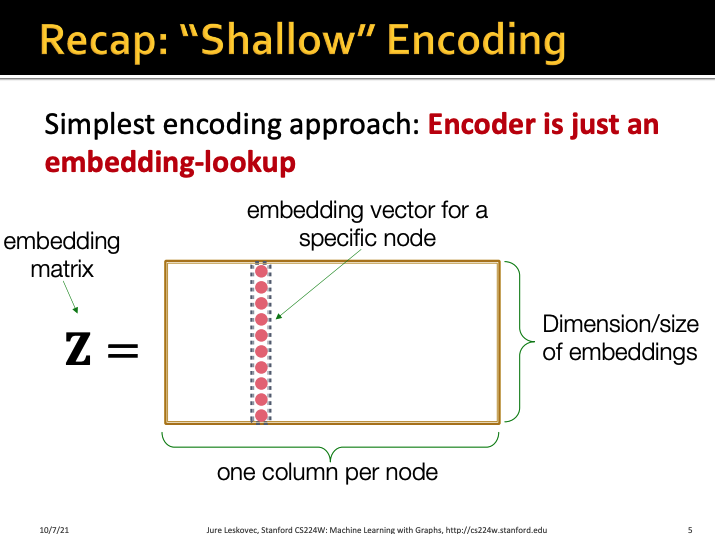
지난 시간에 Node embedding에 대해 배우면서
아주 간단하게 embedding 할 수 있는 방법인
shallo encoding에 대해서 배웠다
embedding matrix Z가 있으면
한 개의 column이 노드 1개를 나타낸다
그래서 전체 행의 개수는 전체 노드의 개수
전체 열의 개수는 각 노드의 embedding size가 된다

그러나 이렇게 간단한 shallow encoder도
당연히 단점이 존재한다
우선 많은 양의 파라미터가 필요로 한다는 점이다
노드 간에 파라미터를 공유하지 않기 때문에
파라미터는 노드개수 * 차원만큼 필요하다
또한 transductive한 방식인데
이게 무슨 뜻이냐 하면
훈련 때 본 것에 대해서만 임베딩을 할 수 있어서
새로운 노드가 들어오면 임베딩을 할 수 없다는 뜻이다
이와 반대로 전체를 추론하는 방식이라
새로운 노드가 들어와도 해당 노드의 feature를 추론해서
임베딩이 가능한 것을 뜻한다
아무튼 이러한 shallow encoder 방식은
transductive한 방식이고
우리가 앞에서 배운 deepwalk나 node2vec도
transductive한 방식이라
노드 속성 등을 활용하지 못하고
이러한 방식은 새로운 데이터가 다양하게 생성되는
소셜네트워크나 추천시스템에서는 제약이 커진다

오늘 배울 내용은 Deep Graph Encoder이다
결국 우리가 Graph Neural Network를 수행하는 과정은
그래프를 input으로 넣으면 multiple layers를 거쳐서
우리가 원하는 예측값인 output이 나오게 되는 것이다
deep graph encoder는 이러한 multiple layers를
어떻게 생성하는지에 대한 내용이다
이러한 deep graph encoder는 우리가 이전 시간에 배웠던
deepwalk나 node2vec과 같은
node similarity function도 모두 포함하는 개념이다

그렇다면 지금 우리가 배울 GNN은
지금까지 연구된 현대의 Machine Learning들과 뭐가 다를까?
가장 크게 다른 점은 지금까지의 machine learning은
simple한 data들을 input으로 넣었다는 점이다
보통 linear하거나 sequence한 데이터들을 주로 다뤘다
하지만 그래프와 같은 네트워크는 매우 복잡하다

grid같은 경우는 locality가 존재한다
이게 무슨 말이냐면 grid같은 경우는
어떤 노드(?) 기준으로 다른 노드는
top, left, right에 존재한다와 같은 지역성이 존재하지만
graph에는 그런게 없다

따라서 이번 강의의 내용은
1. graph를 위한 deep learning
2. GCN
을 배운다
내가 들은 강의의 버전에서는 3이 GraphSAGE 내용인데
ppt는 최신버전이라 내용이 바뀌어있다...ㅎ
우선 본격적인 내용에 들어가기전에
Deep Learning에 대한 기본적인 내용을
간단하게 복습한다고 한다

machine learning에서 목적은
loss function L의 값을 최소로 만드는 것이고
그 loss는 보통 모델 예측값과 정답값의 오차이다

loss function의 예시이다
분류 문제에서 자주 사용하는 loss function은
cross entropy이다
c가 분류되는 class의 개수이다
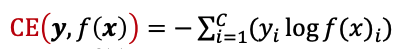
따라서 전체 training dataset에 대해서 loss를 계산하면

위와같이 된다

위에서 정의한 loss함수가 가장 낮은 값으로 수렴할 때까지
weight를 반복해서 계산한다
가장 적절한 weight를 찾는 과정에서
gradient step을 조절하는 하이퍼파라미터인 learning rate를 설정해준다

이번엔 SGD에 대해서 간단하게 살펴보자
기존의 gradient descent를 계산할 때에는
전체 dataset에 대해서 정확한 계산이 필요하다
하지만 SGD는 minibatch로만 계산하면 되어서
계산의 효율성을 높일 수 있다

batch size나 iteration, epoch과 같은 개념 설명은 생략하겠다
하지만 이런 SGD의 단점은
수렴에 대한 보장이 없다는 점이다
따라서 이런 SGD를 개선하기위해서
Adam, Adagrad 등과 같은
다양한 변형의 optimizer들이 나오기 시작했다
딥러닝에 대한 내용은 이정도로만
아주 간단하게 복습하고 다시 graph neural network로 돌아가보자

이제서야 진짜 시작하는
Deep Learning for Graphs...

용어를 간단하게 정리해보자
graph G에 대해서
노드의 집합은 V
그래프 구조를 나타내는 인접행렬은 A
node features 행렬은 X
그리고 각 노드는 v이고
해당 노드 v의 이웃 노드는 N(v)이다
node features로는 위와 같이
social network에서는 프로필
bigological network에서는 유전자 프로필 등이 있다
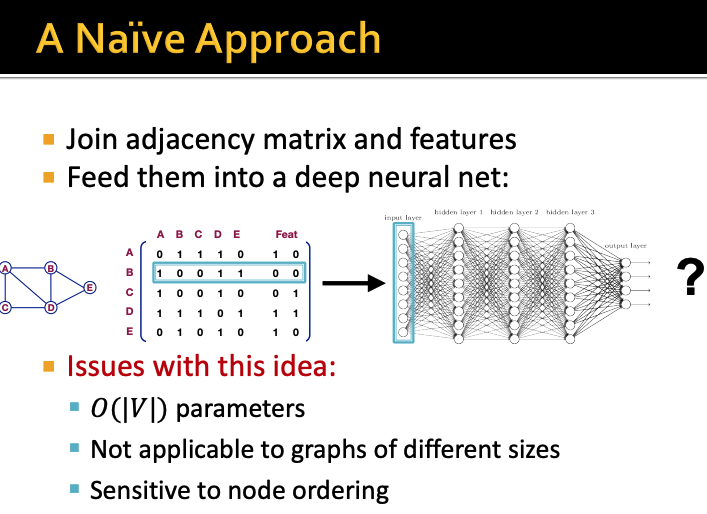
아주 나이브한 방법으로 우선 생각해보자
아주 간단하게는 그냥 인접행렬과 feature 행렬을
join하면 되는 것 아닐까?
하지만 이렇게 해버리면
전체 파라미터는 노드 개수만큼 나오게 되고
다른 size의 graph에는 적용할 수 없게 되며
node ordering에 예민해진다

따라서 idea를 이미지를 다룰 때 쓰는
convolutional network에서 따왔다
이미지에서 사용되는 CNN을
graph로 generalize 시킨 것이다
CNN에서는 slide window라는 개념이 있다
이 slide window 단위로 잘라서
내부에서 compute를 하게 되는데
이를 graph에도 적용하는 것이다

하지만 위와같이 실제 그래프에서는
slide window로 자르는게 쉽지 않다

graph는 permutation invariance하다
이 말은 즉슨 graph는 어떤 일련의 순서가 없다는 뜻이다
그래프에서 어떤 노드가 존재하는데
해당 노드에 순서를 부여할 수는 없다
따라서 Image처럼 window를 생성할 수가 없다

이러한 graph의 특성 때문에
Graph Neural Network에서는
한 노드의 이웃들의 정보를 passing하고 aggregate하는 방식을 사용한다
이는 image에서 CNN이 window의 픽셀 정보를
aggregate해서 1개로 만드는 것과 유사한 방식이다

이제 마지막으로 Graph Convolution Networks를 배워보자

예를 들어서 위 ppt에서 빨간 노드를 예측하고 싶다고 하자
그럼 그 빨간 노드의 이웃 노드들로부터 정보를 얻어야한다
그렇다면 이 이웃 노드들의 정보를
어떻게 propagate 할 수 있을까?

위 ppt에서 예측해야되는 노드는 A이다
그렇다면 A의 이웃 노드인 B, C, D로부터 정보를 받아야한다
그런데 Neural network에서는
multi layer를 구현해야하므로
또 B, C, D 노드는 또 각각의 이웃노드들로부터 정보를 받아야하는 것이다

저 사각형에 해당하는 부분이 layer이다
각 이웃들로부터 information을 얻어서 transform하고
이를 aggregate해서 single message로 만든 다음 passing한다

따라서 GCN은 각 노드별로
이웃 노드를 바탕으로 computation graph를 생성할 수 있다

모델은 arbitrary depth를 가지는데
첫 번째인 layer 0은 해당 노드의
input feature가 된다
k번째 layer인 layer k는 해당 노드로부터
k-hop 떨어진 정보를 받는 embedding이다
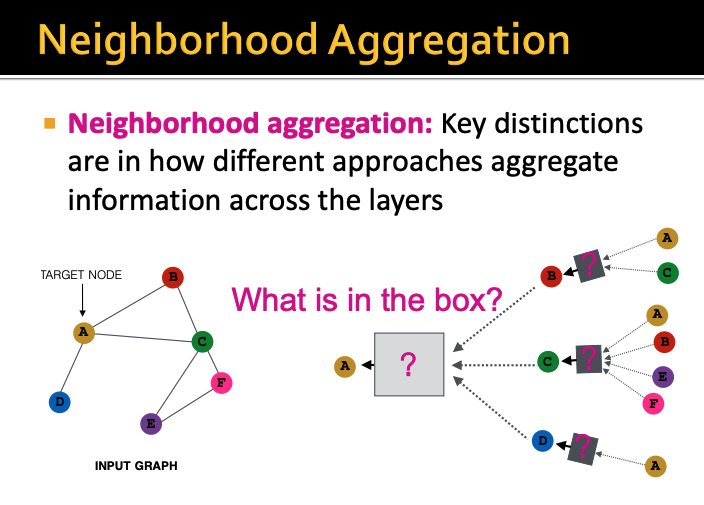
따라서 이렇게 neighborhood aggregation을 할 때
중요한 점은 aggregation을 어떤 방식으로 하는지이다
또한 neighborhood aggregation에서 한 가지 알아야하는 점은
앞에서도 나왔지만 graph에서 order는 무작위라는 점이다
즉, 각 노드를 어떤 순서로 aggregate해도 결과가 늘 같아야한다

GCN의 가장 기본적인 접근은
이웃들에서 모아온 정보들을 평균하는 것이다
평균은 계산 순서를 다르게 해도 순서가 상관없다
위 식을 천천히 살펴보자
0번째 layer에는 노드 v의 feature vector인
Xv를 넣어준다
그렇게 노드 v의 k+1번째 embedding값은
이웃 노드 N(v)의 임베딩값 h에서
이웃 노드의 개수인 |N(v)|만큼을 나눈 나눠준 뒤
해당 v 노드의 k번째 embedding값도 더해준다
그런다음 ReLU같은 non-linearity 함수를 적용해주면
노드 v의 k+1번째의 embedding 값이 나오게 된다
이 모든 과정을 Deep Encoder라고 부른다

그렇다면 이러한 GCN 모델을 어떻게 학습시켜서
embedding을 생성할 수 있을까?

앞에서도 잠깐나온 deep learning 복습에서 설명했지만
결국 우리의 목적은 objective function을
최적화 시키는 것이다
따라서 이러한 objective function을 구성하는
loss function을 정의해야한다
아까 GCN은 aggregation 과정이 평균이라고 했다
따라서 노드 v의 k+1번째 embedding 값은 위 식과 같이 정의된다고 했다
그렇다면 위 식에서 학습 가능한 파라미터는 Wk와 Bk이다
Wk는 이웃들 aggregation weight matrix이고
Bk는 자기 자신의 hidden vector들을 transform하는 weight matrix이다
따라서 이 Wk와 Bk를 loss function에 적용하고
SGD로 파라미터들을 train 시킬 수 있다

aggregation 과정을 행렬 계산할 때
노드별로 이웃 임베딩 평균하는 과정을 반복문으로 하면
굉장히 비효율적이다
따라서 sparse matrix를 이용해서 행렬곱으로 하면
해당 aggregation 과정을 굉장히 빠르게 수행할 수 있다
H(k)는 해당 k번째 레이어에서 모든 노드의
hidden representation을 모아 만든 행렬이다
그렇다면 노드 v의 이웃노드 u의 embedding을 다 더한 값은 결국
인접행렬과 H(k)를 곱한 값과 같아진다
그런 다음 이웃노드의 개수
즉, 차수(degree)로 대각행렬 Dv,v를 만들어보자
D는 diagonal matrix이기 때문에 D의 역행렬도 결국
diagonal하게 되고 그 값은 1/|N(v)|와 동일하다
따라서 모든 노드의 이웃을 평균한 값은 결국
D의 역행렬과 인접행렬과 H(k)를 곱한 값이 된다
이게 k+1번째 layer에서의 모든 노드의 aggregation값이 된다

위에서 알아본 update function을 matrix form으로 다시 작성하면
위와 같이 나타낼 수 있다
k+1번째 layer에서의 모든 노드의 embedding 값은
D의역행렬*인접행렬*H(k)이고
여기서 학습가능한 파라미터 W와 B를 각각 적용해준 다음
비선형함수를 적용해주면 된다
이렇게하면 sparse matrix를 사용해서
행렬곱 효율화가 가능해진다

그렇다면 이렇게 구성한 GNN model을
어떻게 학습시킬 수 있을까
model training에는 크게 2가지로 구분할 수 있는데
정답 라벨을 이용해서 학습하는 supervised learning과
라벨이 없는 unsupervised learning이 있다
supervised learning에서는 node embedding z값을
모델에 넣어서 예측한 f(z)와 실제 정답 라벨인 y와의
loss를 구한 다음 이를 최소화하는 방식으로 학습시킨다
unsupervised learning에서는 graph의 구조를
supervision으로 활용해서 학습시킨다

unsupervised training에 대해서 좀 더 살펴보자
한 가지 아이디어는 유사한 노드는
유사한 임베딩을 갖고 있을거라는 것이다
노드 u, v가 있을 때
yu,v가 1이면 u와 v는 유사하다는 것이다
그리고 DEC는 단순한 dot product이다
따라서 실제 예측값 DEC(zu, zv)과 정답 yuv간의 오차를
cross entropy 손실 함수로 계산한다
node간 similarity는 dot product가 아니더라도
우리가 이전에 배운 다른 것들도 가능한데
random walk, matrix factorization, node proximity등도 가능하다

이제는 supervised learning을 살펴보자
앞에서도 이미 설명을 했지만
node classification이 대표적인 supervised learning이고
실제 정답 라벨이 존재하기때문에 이와 loss를 계산하면된다

node classification에서 정답 라벨은 1 아니면 0의 값을 가진다
따라서 만약 정답이 0이면 두번째 항만 계산이 되는 것이고
정답이 1이면 첫 번째 항만 계산이 되는 것이다

따라서 지금까지 배운 model design을 다시 한 번 정리해보자
우선 첫번째로는 이웃들을 aggregation할 때
어떻게 할 것인지 aggreagation function을 정의한다
그 다음은 각 embedding 값들의 Loss function을
어떻게 설정할 것인지 정의한다

이제 graph를 가지고 각 노드 집합마다
compute graph를 생성한다음
이를 바탕으로 학습시킨다

그런 다음 노드별로 node embedding을 생성한다

여기서 inductive capability라는 개념이 나오는데
잠깐 살펴보고 넘어가자
위에서 우리가 본 학습 가능한 파라미터 W와 B는
모든 노드에 사용되는 shared parameters이다
따라서 W, B는 그래프 크기가 아닌
feature에 의해서 dimension이 정해진다
일반적인 모델은 노드가 많아지면 파라미터 수도 선형으로 증가하는데
위 모델은 모든 노드에 같은 파라미터를 공유해서
노드수보다 파라미터수를 훨씬 작게 유지할 수 있는 것이다
따라서 새로운 노드가 들어와도 그래프 전체가 아닌
이웃노드 정보만보고 aggregation해서
embedding을 생성 가능하다
이러한 이유로 기존에 학습시키지 않았던
unseen node에 대해서도 추론해서
node embedding을 생성할 수 있게된다
이렇게 그래프 전체 구조에 구애받지않아서
새로운 노드가 들어와도 추론이 가능해지는 것을
inductive capability라고 부른다
Graph Neural Network에서의 첫 시간인
Graph Convolution Network(GCN)에 대해
수업을 들은 내용 정리는 여기서 끝 -!
생각보다 길어졌다 ..ㅎ
'강의 > graph neural network' 카테고리의 다른 글
| [GNN] Graph Training (Stacking Layers Problems, Prediction Head, Loss, Evaluation) (0) | 2025.09.03 |
|---|---|
| [GNN] A General Perspective on Graph Neural Networks (GCN, GraphSAGE, GAT) (1) | 2025.09.01 |
| [GNN/Colab 실습] GraphSAGE layer 구현하기 (3) | 2025.08.28 |
| [GNN] Node Embedding 2편 (node2vec) (3) | 2025.07.29 |
| [GNN] Node Embedding 1편 (Random Walk와 DeepWalk) (4) | 2025.07.27 |