본 게시글은
서울대학교 데이터사이언스대학원 이상원 교수님의
데이터사이언스 응용을 위한 빅데이터 및 지식관리시스템 수업을
학습을 목적으로 재구성하였습니다
이번 시간에 배울 내용은
external sorting에 대한 내용이다
external sort는 정확하게 어떤 것이고
그냥 sort랑은 뭐가 다른걸까?
뒤로가면서 궁금증을 풀어보자

이번 챕터를 공부하면서 이해해야 하는 내용은 위와 같다
sorting은 DBMS에서 왜 중요하며
in memory sorting과 external sorting은 어떤 것일까?
그리고 external sorting의 대표 알고리즘인
external merge sort에 대해 살펴보고
B+Tree와 다른 sorting들도 살펴보자

그렇다면 우선 우리가 sorting을 왜 배워야하는지 간단하게 보자
조금은 오래된 내용이지만
1960년대 이 당시의 컴퓨터 cpu 연산의 4분의 1정도는
sorting을 하고있다고해도 과언이 아니라고한다
이정도로 전통적인 컴퓨팅에 있어서 sorting은
매우 중요한 operation이었다
즉, 많은 문제를 해결하기 위해서는
sorting 알고리즘이 필요했다는 뜻이다

우리가 이전시간에 배웠던 B+Tree index를 만들 때도
sorting은 필요하며
join 알고리즘에서도 sorting을 기반으로 동작하는 join이 존재한다
또 hash 기반의 sorting도 존재한다

그렇다면 그냥 sorting도 아니고 external sorting이란 무엇일까?
우리가 컴퓨팅 수업이나 기초를 배우는 시간에
여러가지 sorting 알고리즘을 배웠을 것이다
이는 기본적으로 in-memory sorting algorithm이다
즉, DRAM에서 이루어지는 정렬 알고리즘이라는 뜻이다
하지만 만약에 sorting을 할 데이터는 1기가인데
사용가능한 DRAM은 1MB밖에 없다면?
DBMS에 저장되는 데이터들은 기본적으로 사이즈가 굉장히 크다
따라서 이런 데이터들을 정렬할 때
디램의 부족때문에 데이터를 디스크에 둔 상태로 정렬을 수행한다
따라서 External(외부)라는 이름이 붙었고
이를 external sorting이라고 한다

오라클의 메모리 구조라고한다
저 PGA라는 공간에서
sorting을 수행할 수 있다고한다

위에서 살펴본 메모리 구조를
조금 더 자세하게 살펴볼 수 있는 그림이다
database buffer cache와 PGA
그리고 PGA 내부 content를 살펴볼 수 있다
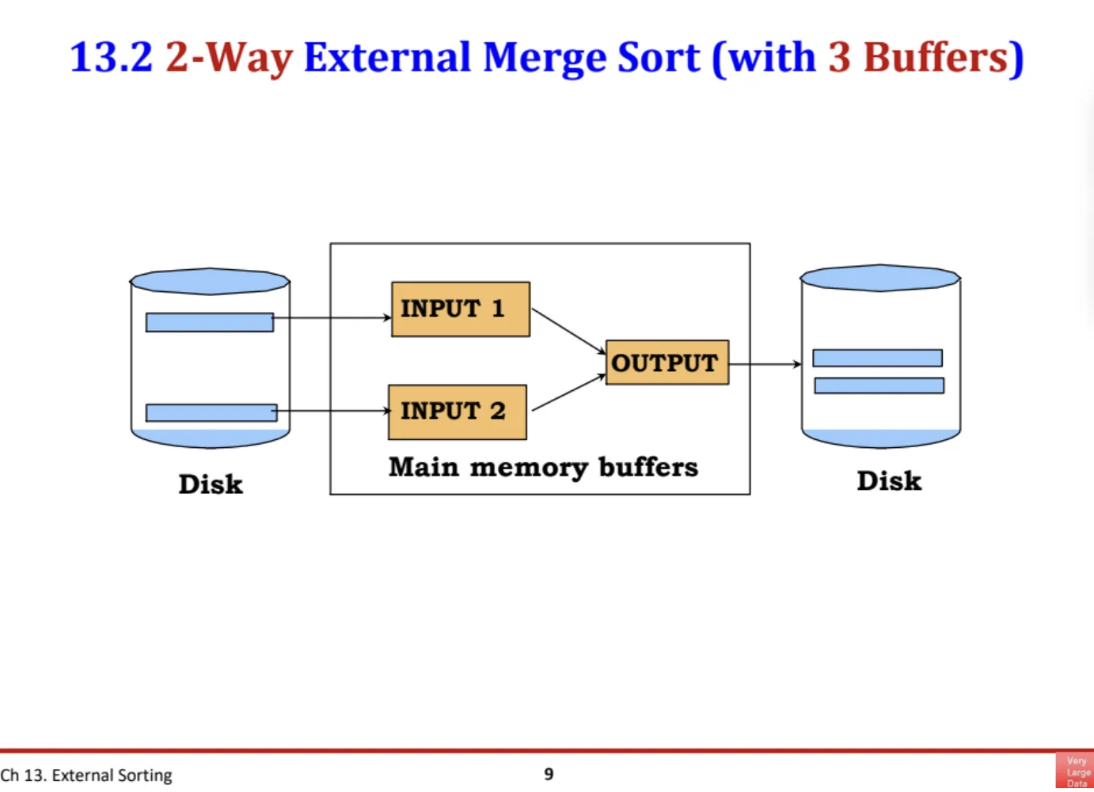
그럼 external sorting의 가장 대표적인 알고리즘인
external merge sort를 살펴보자
이 방법은 아주 naive 한 방법이다
sorting 해야할 파일이 disk에 존재하고
Main memory buffer에서도 동작을 시켜서
최종적으로 disk 파일이 sorting이 되도록 하는 것이다
디스크 내부에 각각의 페이지들이 있는데
페이지 내부에 sorting을 해야하는 레코들들이
몇 십 몇 백개가 정렬이 안된 상태로 존재한다
처음에는 buffer를 1개만 사용해서
그 내부에서 우리가 알고있는 in memory sorting 알고리즘으로 실행한다
그런 다음 sorting이 완료된 페이지를 디스크에 쓴다
그런 다음 또 한 페이지를 읽어서 sorting하고
또 sorting한 것을 디스크에 쓴다
예를 들어 데이터가 1기가가 있고
100MB씩 페이지를 읽어온다면
총 10번을 수행해야하는 것이다

위에서 설명한 방식이
DRAM을 1개만 쓰는
pass0 방식이다
각각의 n page들을 페이지별로 읽은 다음
각각 개별로 sorting을 진행한다
그런 다음 sorting이 된 inpu1, input2끼리 merge를 한다
partially sorting 되어있는 레코드들의 key 값을
각각 비교해서 다시 sorting해서 disk에 쓰는 것을 반복한다
이것을 동시에 input을 k개를 가져갈 때
k-way external merge sort라고 부른다
따라서 k개의 run에 대해서 merge를 해서 한개의 페이지로 만들어
disk에 쓰는 것이다
이 과정을 계속 반복해서 결국 마지막 1개의 파일로 merge가 될 때까지
수행하면 sorting이 끝나게 된다
이는 log2 N만큼의 Pass가 필요하다

구체적으로 동작을 이런식으로 한다
맨처음 pass0에서는 각각의 데이터페이지에 대해서
in memory sorting을 진행하고
각각 2개의 run끼리 merge를 진행한다음
또 거기서 merge를 진행한 run들끼리 merge를 진행해
결국 최종 1개의 sorting된 페이지가 나오게 된다
2N 만큼의 page IO가 발생하고
전형적인 divide and conquer 방식이다

그럼 이제 다른 경우를 한 번 살펴보자
우리가 sorting해야할 파일이 N개의 page로 구성되어있는데
우리의 buffer page는 B개이고
이 B개는 N개보다 작다
우선 pass0에서는 B개의 run을 각각의 buffer에 불러와서
정렬할 수가 있을 것이다
그렇게 되면 생성되는 초기 run의 수는
N / B개가 된다
그 다음 여기서 B - 1개의 buffer가 merge하는데 쓰이고
나머지 1개의 buffer는 run을 읽는데 사용되므로
최대 B - 1개의 run을 병합가능하다

따라서 전체 pass 수를 계산하면
위 ppt에 나온 것과 같다
그러고 Cost는
2N * pass의 개수가 된다

이러한 external sort는 디스크 IO를 줄일 수 있지만
굉장히 CPU intensive한 연산이다
그래서 중간에 메모리를 조금 더 투입해서
비교 연산을 적게 하면서
CPU intensive를 줄이기도 한다

그다음 CPU에 가해지는 부담을 줄이기위해
selection tree를 사용해서 merge를 수행하기도 한다
selection tree를 사용하게 되면
comparison이 log 2의 B-1이 되어서
횟수가 굉장히 많이 줄게된다

external sorting에서는
여러 run을 동시에 쓰고 디스크에 쓰는 과정에서
디스크 접근에 병목이 생기는 경우가 많다
따라서 이를 해결하기 위해서
한 번에 하나의 페이지가 아니라
여러 개의 페이지를 묶어서 읽고쓰는 방식을
blocked IO라고 한다
이렇게하면 전체 buffer의 개수가 B 개이고
한번에 b개씩 입출력을 한다고 하면
총 (B-b)/b개를 병합할 수 있다
하지만 이렇게하면 trade off가 당연히 발생하는데
Blocked IO 방식을 이용하면
병합할 수 있는 run의 개수가 줄어들기 때문에
총 Pass 수가 결국 증가할 수가 있다

N은 전체 페이지의 개수
B는 buffer page의 개수이고
하나의 IO block은 32 페이지로 구성되어있을 때의
각 전체 페이지와 buffer page의 개수별
pass 횟수를 나타낸 표이다

한 pass에서 merge를 할 때
disk IO 비용이 얼마나 드는지는
B와 b를 어떻게 세팅하냐에따라 달라진다
cluster size = blocking factor라고도 하는데
내가 한 번 merge할 때 얼만큼 할 것인지를 나타낸다
b가 커지면 # of pass는 증가하게 되고
IO cost / pass는 감소하게 된다
따라서 optimal cluster size는
두 항목간의 균형을 잡아주는 곳에서 결정된다

또 double buffering이라는 방법도 있다
(교수님 목소리가 잘 안들려서
사실 정확하게 이해가 잘 안됬..)
external sorting에서 데이터를 merge할 때
각 run을 입력 buffer에 넣고 처리한다
하지만 입력 버퍼가 모두 읽히면
다음 데이터를 디스크에서 가져와야하기때문에
CPU는 그때까지 기다려야하고
이로인해 지연시간이 발생한다
한마디로 double buffering은
이 disk IO에서 오는 지연시간을 줄이기 위해
buffer를 2개를 두는 방법이다
현재 버퍼가 데이터를 읽고있는 동안
shadow buffer라고 불리는 다른 버퍼에
다음 데이터를 미리 대기시켜놓는다
따라서 이 방법은 총 처리량보다는 response time을
줄이는데에 초점을 맞췄다고 할 수 있다

그렇다면 이전시간에 배운 B+ tree에서
sorting을 사용해보자
우리가 앞에서 배웠듯이 B+Tree는
이미 정렬이 되어있는 데이터들이기 때문에
단순하게 생각하면
leaf nodes를 왼쪽부터 읽으면
정렬된 데이터를 가져올 수 있을 것이라고 생각할 수 있다
하지만 여기서 중요한 것은 clsutering이다
clustering이 제대로 안되어있으면
B+Tree에서 정렬된 데이터를 읽어와도
실제로 디스크에서 데이터를 가져오는데에는 시간이 걸린다
따라서 만약에 clsutering이 제대로 되어있지 않다면
우리가 지금까지배운 external sorting 알고리즘을 사용하는 것이
더 효과적일 수도 있다
external sorting의 내용은 여기까지이고
이후에 evaluation of relational operators에 대한 내용을
더 수업해주셨는데
아주 조금만 하고 다음 수업에서 본격적으로 다루기 때문에
해당 내용을 합칠 생각이다
그리고 .. 요즘 교수님이 마이크를 잘 안쓰시는데
정말 마이크를 안쓰시면 뭐라고하시는지 정말 하나도 안들려서
수업 내용을 따라가기가 힘들다 ..
ㅋㅋㅋㅋㅋㅋㅋ
아무튼 최선을 다해보려고한다
화이팅-!
'강의 > database' 카테고리의 다른 글
| [database] simpleDB로 buffermanager에서 LRU 알고리즘 구현하기 (2) | 2025.05.27 |
|---|---|
| [database] Physical Query Algorithm & Query Optimization (0) | 2025.05.26 |
| [database] B+Tree Index의 insertion과 deletion (+hash indexing) (1) | 2025.05.25 |
| [database] Tree-Structured Indexes (ISAM과 B+ Tree) (5) | 2025.05.25 |
| [database] DBMS와 Disk, Buffer Management(LRU) (2) | 2025.05.10 |