본 게시글은
서울대학교 데이터사이언스대학원 성효진 교수님의
데이터사이언스를 위한 컴퓨팅 시스템 강의를
학습을 목적으로 재구성하였습니다
지난번 시간에 이어
두번째 시간
string과 float 타입에 대한
저장방식에 대한 내용이다

컴퓨터 내에 저장되는 모든 data들은
0과 1로 저장된다
우리가 사용하는 컴퓨터 내의 프로그램이라고 하는 것은
프로그램의 코드가 저장되어있는 메모리 address에
access할 수 있는 0과 1의 data들의 연속이라고 할 수 있다
즉, 한 개의 프로그램은
굉장히 커다란 byte 단위의 array들의
연속이라고 생각하면 좋다
단, 우리가 보기에는 연속적인 공간에 있는 것처럼 보이지만
실제 하드웨어적으로 연속은 아니다
하지만 conceptual하게 연속적으로 저장되어있다고
생각해도 무방하다
개발자인 우리가 컴퓨터 프로그램을 작성하면
컴파일러나 os의 메모리 관리자들이
주솟값을 할당하고 값을 access 할 수 있도록 해준다
우리가 컴퓨터에서 어떤 프로그램을 실행하면
마치 하나의 process가 자신만의
독립적이고 고유하고 커다란
주소 공간을 갖고있는 것과 같은 환상을 준다
실제로 운영체제는 우리 컴퓨터에서 실행되는
수많은 프로그램들이 컴퓨터의 자원을
적절히 공유해서 사용하게한다
하지만 사용자가 느끼기에는
내가 실행시킨 process가
os와 메모리를 독점해서 사용하는 것처럼 보인다
이러한 것을
운영체제의 virtualization이라고 한다
이런식으로 하드웨어와 같은 컴퓨터의 자원관리를
운영체제가 하는 이유는
프로그래머가 메모리 관리를 하게 한다면
컴퓨터를 사용하는 것이 너무 어려워지고
의도와 다르게 다른 데이터를 훼손할 수 있는
보안의 문제도 발생할 수 있기 때문이다

이전 수업시간에 word 단위에 대한 내용이
잠깐 언급된 적이 있는데
int는 4byte이고 이는 word 단위의 크기이다
word는 주소의 단위이고
컴퓨터가 한 번에 처리할 수 있는
기본 데이터의 크기이다
이전에는 32bits를 word단위로 사용하는
32bits machine을 주로 사용하였다
하지만 주소공간 부족 문제가 생기며
32bits에서 64bits로 주소의 단위인
word단위를 확장시켰다
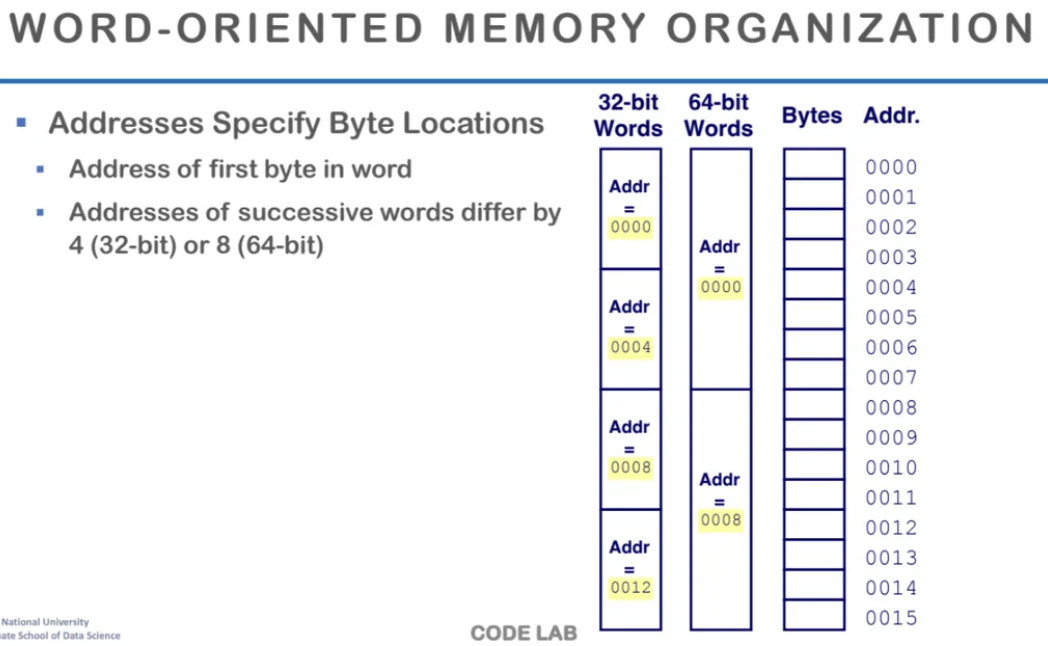
32bits와 64bits에서
메모리 저장 방식의 차이이다
32bits에서는 4byte가 기본 word의 단위라
4byte씩 띄워서 저장되는 것을 볼 수 있다
64bits에서는 8byte씩 저장되는 것을 볼 수 있다
노란색으로 형광펜이 그어져있는(?) 주소는
word단위의 제일 처음 byte의 주솟값이다
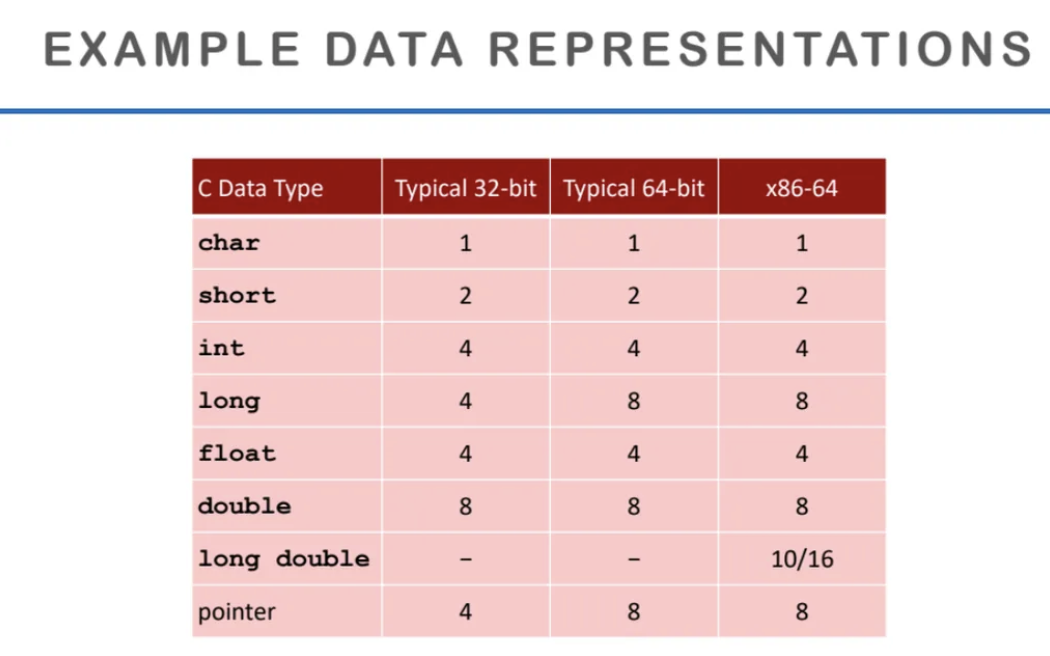
이전 수업시간에서도 나왔던 표인데
32bits, 64bits machine 별로
데이터를 표현하는 크기이다
여기서 주목해야할 것은 pointer의 크기이다
pointer는 address 공간의 크기 정보를 담기 때문에
32bits에서는 4byte, 64bits에서는 8byte인 것을 확인할 수 있다

그렇다면 byte를 memory에 어떻게 저장하는지 알아보자
역사적으로 Sun, PPC Mac과 같이
Big Endian이라는 방식을 쓰는
하드웨어들이 있었다
하지만 이는 예전 하드웨어들이고
우리가 쓰고있는 대부분의 하드웨어들은
Little Endian 방식으로 byte를 저장한다
Big Endian과 Little Endian 방식의 차이는 간단한데
가장 작은 byte를 가장 큰 주소에 넣으면 Big Endian
가장 작은 byte를 가장 작은 주소에 넣으면 Little Endian 방식이다
한 가지 기억하면 좋은 점은
인터넷 프로토콜이 데이터를 transmit 할 때
아직까지 Big Endian 방식을 사용하고 있다는 점이다
그래서 Little Endian 방식과
Big Endian 방식의 호환이 중요하다

예시를 통해 Big Endian과 Little Endian 방식의
차이를 살펴보자
0x01234567 이라는 4byte를 저장해보자
주소는 오른쪽으로 갈수록 커지는데
이걸 그대로 넣으면 Big Endian방식이고
역으로 뒤집어서 넣으면 Little Endian 방식이다
01이라는 값이 가장 큰 값인데
Big Endian에서는 가장 작은 곳에 들어가고
Little Endian에서는 01이라는 가장 큰 값이
가장 큰 주소에 들어가는 것을 볼 수 있다
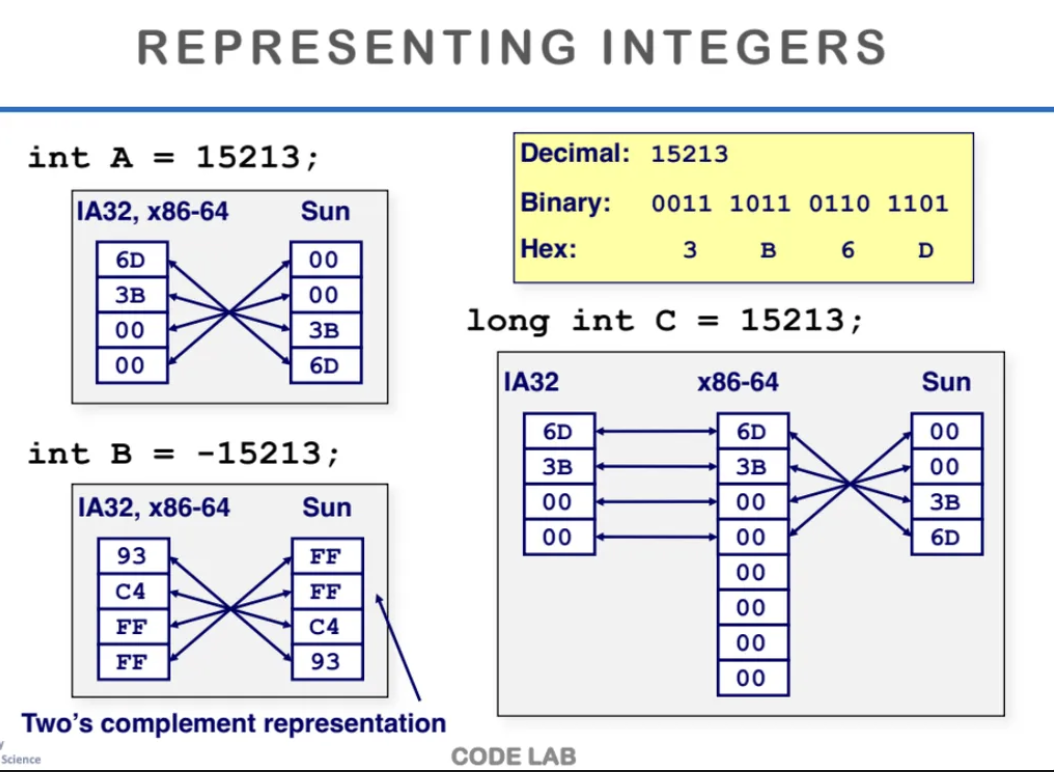
IA32, x86-64는 가장 대표적인 intel의 아키텍처이다
Little Endian 방식을 사용해 byte를 저장한다
ppt의 가장 위를 보면 15213이라는 int를 저장할 때
Little Endian 방식을 활용해서 거꾸로 뒤집어
저장하는 것을 확인할 수 있다
음수값을 저장할 때도 마찬가지이다
2의 보수도 거꾸로 뒤집어서 저장한다
long int를 저장하는 방식도 살펴보자
IA32는 32bits machine이고 x86-64는 64bits machine이다
64bits machine에서는 8비트로 표현하기 때문에
남는 값도 0으로 표현하는 값이 많다
이걸 Sun 이라는 하드웨어로 저장하면
Sun은 Big Endian으로 저장하기 때문에
다시 순서가 뒤집혀서 저장되는 것을 확인할 수 있다

우리 컴퓨터가 byte를 어떻게 저장하는지 확인하기위해
c언어 코드를 작성했다
포인터를 이용해서 변수를 뜯어보는 코드가
위 ppt의 코드이다
코드를 간단하게 살펴보면
pointer 변수를 unsigned char로 casting했다
1바이트씩 있는 어떤 char data가 있고
그 데이터를 첫 번째로 reference하는 pointer 변수를
정의한 것이다
print되는 값을 찍어보면 16진수의 값을 출력한다
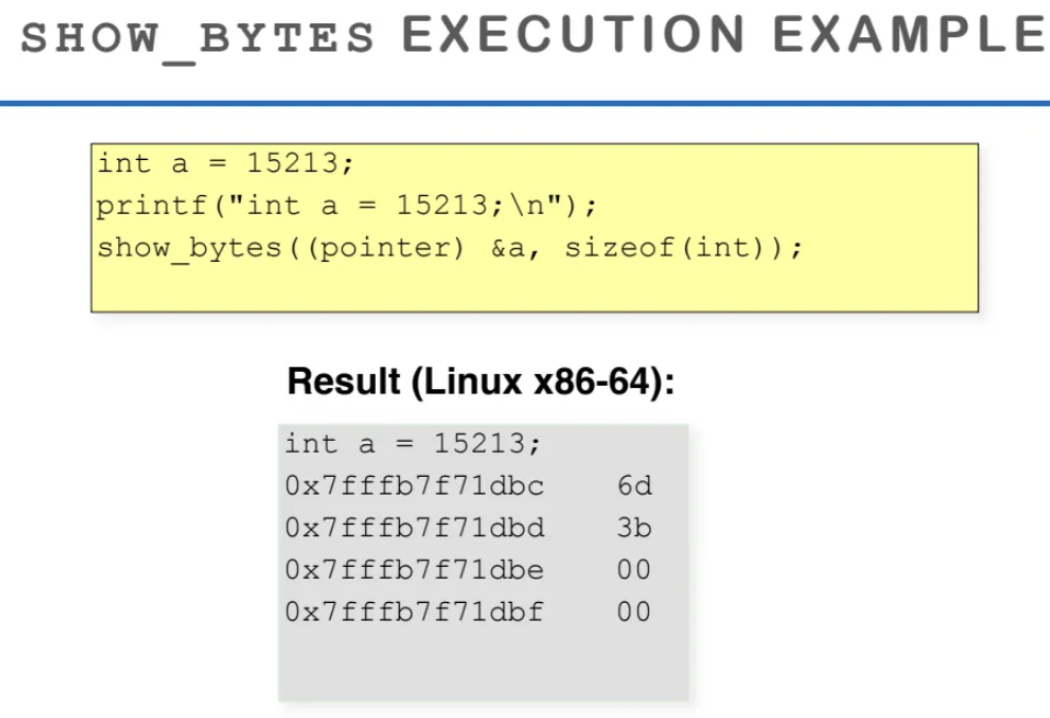
실제로 리눅스에서 해당 코드를 실행시켜보면
변수가 저장된 주솟값들이 위처럼 찍힌다
주소를 자세히보면 1칸씩
증가하고 있는 것을 볼 수 있다
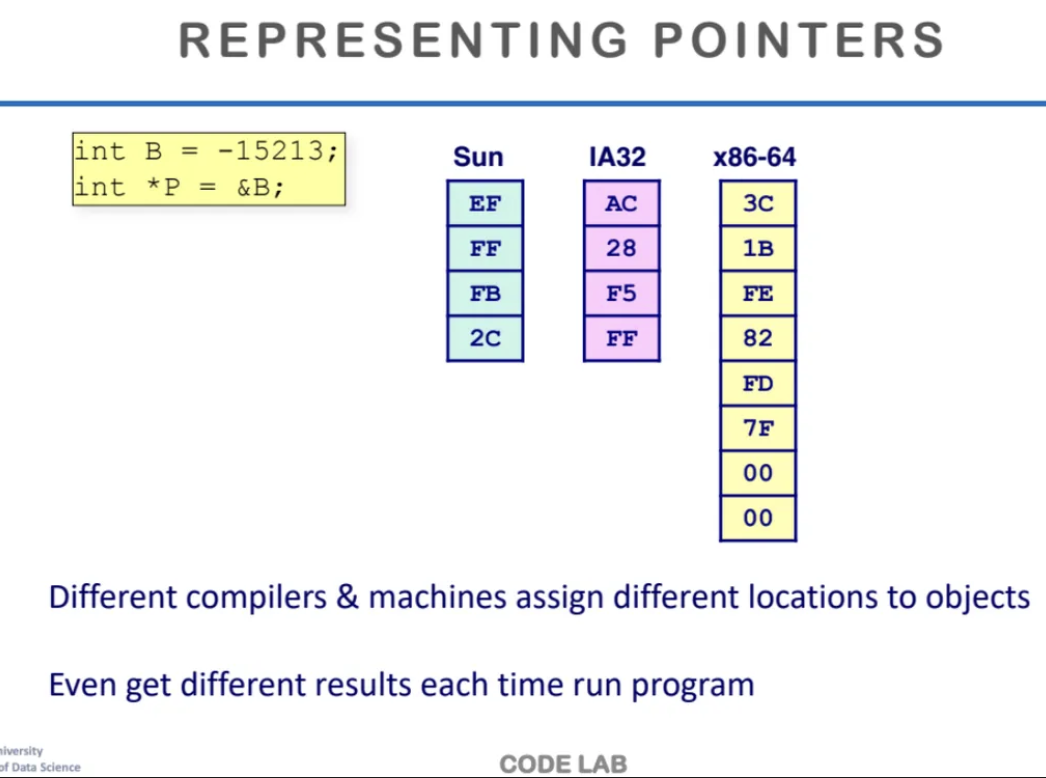
각 하드웨어 별로 포인터 변수가
어떻게 저장되는지 알아보자
-15213인 B값을 저장한 다음
그 B의 주솟값을 p 포인터에 저장한다
Sun과 IA32는 32bits 머신이라
word가 4개, x86-64는 64bits machine이라
word가 8개이다
포인터변수 p는 위 ppt 처럼 저장되게 된다
그리고 pointer에 저장되는 주솟값은
virtual address이기 때문에
실행할 때 마다 다른 값이 나온다

C언어에서 string을 어떻게 표현하는지 알아보자
c++에서는 우리가 사용하기좋게
string이 정의되어있지만
c언어에서는 구현되어있지 않고
하드웨어적으로 string이 어떻게
구현되어있는지 살펴보자
컴퓨터가 이해할 수 있는 것은 결국 0과 1밖에 없기 때문에
문자도 결국 0과 1로 저장해야한다
그렇기 때문에 문자도 결국 숫자로 저장되어야하고
이렇게 어떤 문자는 어떤 숫자로 저장하자는
표준이 정해져있다
이게 바로 문서 프로그램에서 종종 봤던 ASCII이다
아스키는 7개의 bits를 이용해서
기본적인 알파벳 등을 표현한다
특수문자는 아스키에는 없고
더 확장된 다른 유니코드같은 표준에 있다
각 문자별 번호가 다 지정이 되어있고
그 포맷으로 쓰게되면 문자를 표현할 수 있다
그렇다면 7비트로 문자를 표현하면
마지막 1개의 비트는 뭘로 쓸까?
이건 바로 문자가 끝났음을 알리는
null-terminating을 하는 역할을 한다
null-terminating을 하지 않으면
string이 끝난지 모르기 때문에
마지막 비트에 00을 넣어줘서
string이 끝임을 알려줘야한다
string을 저장할 때는 우리가 앞에서 배웠던
Little Endian이니 Big Endian과 같은
byte ordering과는 상관이 없다
byte ordering은 수를 표현하기 위한 방법이고
string은 그냥 우리가 정한대로 저장한다
MSB, LSB의 개념도 없다
크고 작음의 개념이 없기 때문이다
string에서는 왼쪽으로 오른쪽으로
그냥 byte를 저장한다

Disassembly는 기계어를 사람이 읽을 수 있는
assembly 코드로 확인하는 것을 말한다
disassembly 과정에서
바이트를 어떤 순서로 해석하는지 알아보자
위 코드는 0x12ab라는 값을
메모리에 저장하는 코드를
assembly로 바꾼 것이다
0x12ab라는 값이 어떻게 해석되는지 알아보자
우선 값을 32비트로 패딩해서
앞에 0000을 넣어준다
0x000012ab가 되었으면
이를 바이트 단위로 쪼개서
00 00 12 ab가 된다
이를 Little Endian 방식으로 저장하기 때문에
역순으로 뒤집어서
ab 12 00 00 으로 저장한다

이제 floating point에 대해서 알아보자
한국어로는 부동소수점이라고 한다
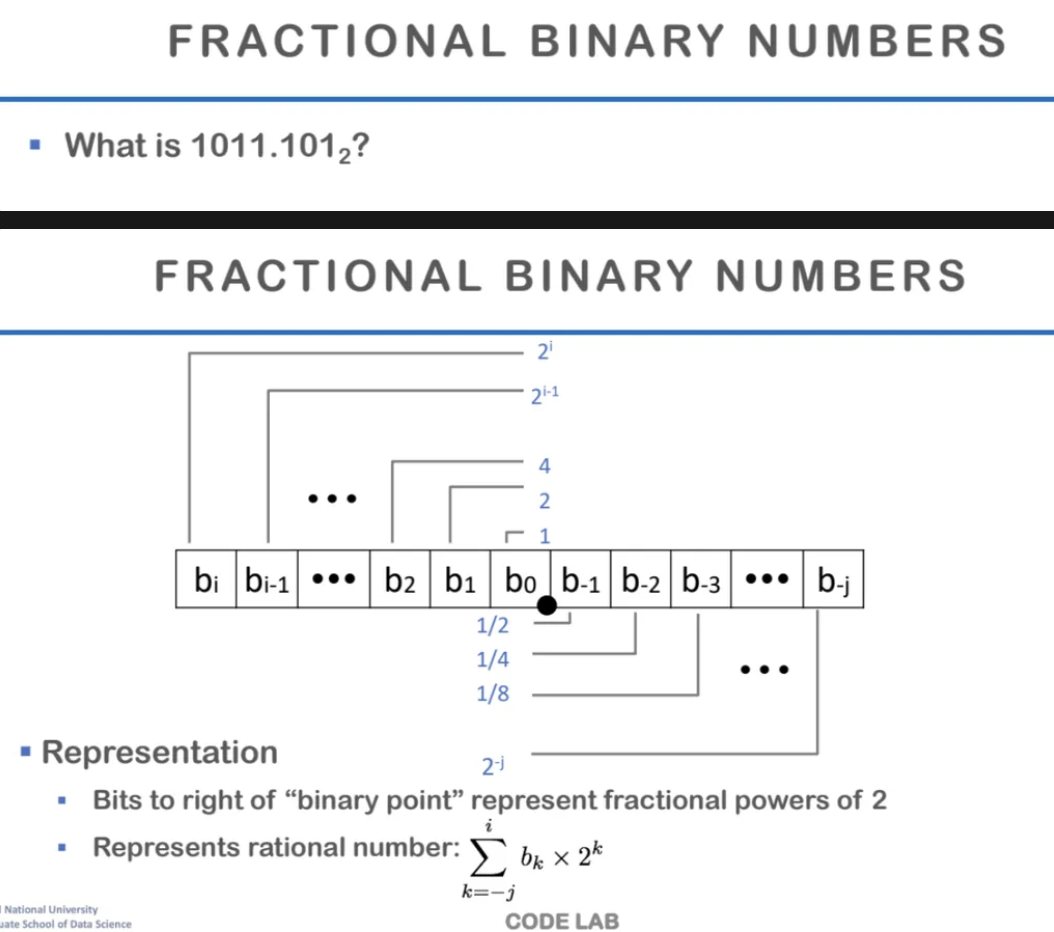
1011.101를 2진법으로 표현하면
어떻게 될까?
위 ppt에 나와있는 binary 방식으로
표현할 수 있는데
오른쪽으로 갈수록 작아지는 분수값이고
b0을 기준으로 분수 부분을 표현한다
2의 제곱에 해당하는
fraction 값으로 각 부분을 표현하고
이렇게 소숫점 이하의 수를 표현하는 방식을
fiexed point(고정 소수점)이라고 한다
고정 소수점은
점을 딱 정해놓고 왼쪽 10개는 정수부
오른쪽의 6개는 소수부와 같은 방식으로
표현하는 방식이다
우리가 뒤에서 배울 floating point인
부동 소수점과 대비되는 개념으로
부동 소수점은 그렇게 몇 개를 정수, 몇 개를 소수로
하겠다는 것을 정해놓지 않은 개념이다
그렇다면 이런 fixed point로 소수를 표현하면
어떤 장점이 있을까?
fixed point 연산시 하드웨어를 구현할 때
불확실성이 줄어든다
정수부와 소수부가 고정되어있기 때문에
하드웨어를 통한 연산에서 편하다
하지만 단점으로는 당연하게도
표현할 수 있는 값의 범위가 굉장히 제한되고
값의 정확도도 제한된다
하지만 요즘은 소수점 이하의 값이
그렇게 정밀할 필요가 없는 경우가 많아
fixed point를 자주 쓴다고 한다

위 ppt는 왼쪽의 10진수를 2진수로 표현한 것이다
위 예시는 정확하게 나누어 떨어지는 값들이다
2의 단위로 나눌 때는 오른쪽으로 shift하고
곱할 때는 left로 shift한다
무한대로 가는 binary 숫자는 쭈욱 가서 무한히 더하는 것이기 때문에
0.111111111... 과 같은 숫자는 1.0 보다 살짝 작은 수를 뜻한다
이를 입실론을 써서 표현한다

위 ppt는 딱 나누어 떨어지지않는 수를
2진수로 표현한 것이다
[01]과 같은 표현은
이 부분이 계속해서 반복된다는 뜻이다
비트수를 고정해놨기 때문에 표현할 수 있는
수 자체가 제한적이다

그래서 우리는 IEEE Standard 754 방식의
floating point 표준을 사용한다
실제로 우리가 사용하고 있는 대부분의 하드웨어는
floating point를 이 표준에 맞게 구현한다
실제로 숫자를 굉장히 정확하게 표현하는 방식이지만
하드웨어에서 연산을 하기에는 까다롭다
직관적인 비트 단위의 연산이 아니라
몇 번의 연산을 더 거쳐야하는 것들이 생기기 때문이다
floating point의 연산을 위해서
FPU라는 하드웨어가 따로 있는데
실제로 ALU보다 훨씬 오래 걸린다
그래서 이를 최적화하는 연구가
많이 진행됐었다

floating point의 표현법을 구체적으로 알아보자
int와 동일하게 MSB는 부호를 나타낸다
floating point에서는 exp와 frac이 있는데
fraction(frac) = matissa = significand 라고도 부른다
세 용어 모두 똑같은 용어이다
exponent는 굉장히 작은 값이며 범위도 작다
굉장히 넓은 범위에 있는 floating point를 표현하기 위해서
weight를 더 하는데
exponent는 그 weight 값이다
2의 제곱으로 표현되며 양수, 음수를 다 포함한다
exp와 frac을 우리는 "encoding"한다는 표현을 쓰는데
이걸 왜 encoding이라고 표현하냐면
정확하게 그 값을 넣어주는 것이 아니기 때문이다
정확한 값을 각각에 넣어주는 것이 아니지만
넣으면 그 값으로 해석이 되는 구조이다

floating point를 표현하는 표준 구조이다
intel만 지원하는 80bits로 가면
exp와 frac의 값이 둘다 커진다

요즘 딥러닝 학습에 많이 사용되고있는
half precision (FP16)과
Vrain floating-point(BF16)이다
BF16은 google이 제안한 것이고
floating point 연산의 구조를 따르지만
exp와 frac의 비율 차이이다
BF16에서는 exp가 더 크고
frac이 더 작다
위 구조가 딥러닝 학습에서 많이 사용되는 이유는
학습에 사용되는 가중치의 값을 정확하게 표현하기보다
정확도를 줄이고 속도를 올리는 방식을
자주 택하기 때문이다

normalized (정규화)에 대해서 알아보자
Exponent의 값은 양수와 음수를 다 표현할 수 있어야하지만
실제로는 다 양수로 표현한다
이런걸 biasing이라고 하는데
이렇게 하는 이유는
exp 자체는 굉장히 작은 수와 큰 수를 다 포함할 수 있어야 하지만
음수를 표현하는 방식인 2의 보수 자체는
비트 표현으로 봤을 때 큰 값인지 작은 값인지를
단순하게 비교하기가 어렵다
그래서 비교를 할 때 빠르게 비교하기 위해서
exponent 부분을 unsigned value의 패턴으로 정의한다
이렇게 되면 숫자를 비교할 때
그냥 1이 더 먼저 나오는 것이 크다고 판단할 수 있다
따라서 이렇게 Unsigned value로 표현하기 위해서
실제 E 값은 exp에서 bias 값만큼 빼면 나온다
normalized (정규화)는
Matissa의 첫 번째 비트가 항상 1이 되도록
조정한 방식이다
그냥 맨 앞에 1이 붙어있다고 가정하는 것이고
fraction bit만 표현하는 것이다
fraction bit가 전부다 0이면 맨 앞에 1을 제외한
모든 수가 0이 되는 것이니까
그냥 1이 되는 것이다
fraction bit이 전부 1이면 2에 무한히 가까운 수가 될 것이다
우리는 이런 것은 leading bit라고 하는데
실제 bit 상으로는 1이 없지만
1이 있다고 가정하고 계산하는 것을 말한다
그래서 이런 것들이 실제 bit 표현과
실제 값이 다른 이유이다

위는 normalized encoding의 예시이다
살펴봐야할 점은
Exp가 140이라고 되어있지만
실제 value는 exp - bias 값이다

denormalized value에 대해서 알아보자
leading bit가 1이 아니고 0일 때인데
이건 특수한 케이스이다
값이 0에 무한히 가까운 아주 작은 값일 때
정밀하게 표현하기 위해서
denormalized value를 사용한다
그래서 exp가 전부 0이면 denormalized 된 형태로 해석해야한다
E = 1 - Bias로 표현한다
significand의 leading bit가 0이라서
0.xxxx 부분이 전부다 fraction이 되는 것이다
그래서 significand가 전부다 0이면
그냥 0이 되는 것인데
여기서 이전 수업시간에 배웠던
2의 보수 표현에 대해 잠깐 떠올려보자
음수를 2의 보수로 표현하게 된 이유는
MSB로 부호로 표현하게 되면
0을 표현하는 방법이 2개가 된다
따라서 이걸 피하고자
음수를 2의 보수로 표현하게 되었는데
위 방법에서는 +0과 -0 그냥 2개를 사용한다

숫자가 0이거나 1인 특수한 상황을 제외하고는
모두 normalization을 시켜줘야하는 조건이 있다
그런데 이런 normalized와 denormalized를 제외하고도
특별하게 표현하는 special values가 있다
그럼 exp가 다 1일 때는
floating point를 표현하는 값 중
어떤 에러 상태가 있다는 것을 표현한다
이런 에러 경우 중 하나는
계산을 했더니 숫자가 무한대인 경우가 있다
이런 경우는 exp가 다 1이면서 frac이 0인 경우인데
이건 우리가 계산할 수 있는 범위를 넘은 상태인거고
overflow가 된 상황이다
그런데 exp는 다 1이지만 frac이 다 0이 아닌 경우도 있다
이건 우리가 계산을 잘못했을 때 나오는 NaN 값이다
계산을 할 수 없을 때 나오는 값이고
어떤 수치적인 값을 계산할 수 없을 경우
이와 같이 NaN으로 표현한다
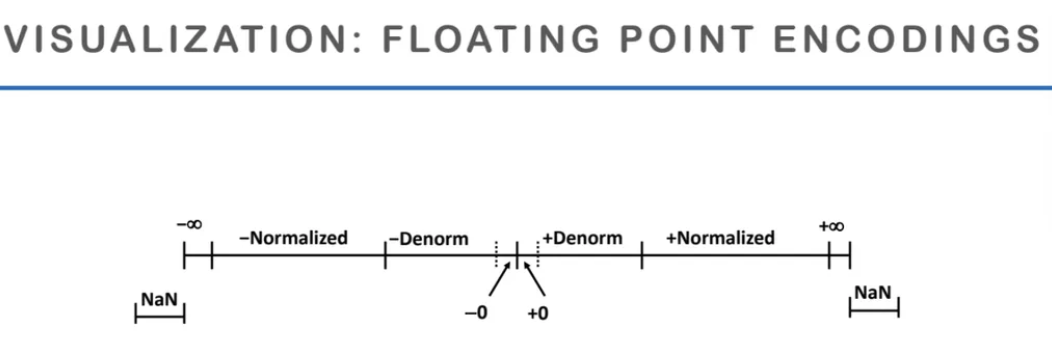
지금까지 앞에서 설명했던
floating point encoding을
시각화 한 것이다
0을 표현하는 방법은 2가지로
-0과 +0이 있다
그리고 그 0의 양쪽으로는 denorm 값이 있는데
(leading bit가 0인 경우)
그 denorm이 표현할 수 있는 범위를 넘어서면
normalized 된 값으로 수를 표현하고
(leading bit가 1인 경우)
그 normalized 된 범위도 넘어서면 -무한대, +무한대가 되고
그 것도 넘어서면 NaN이 되는 것이다

작은 floating point를 표현하는
tiny floating point를 알아보자
원래 기본 정밀도인 single precision에서
precision을 줄여서 실행시간을 줄이는게
요즘의 트렌드라고 한다
tiny floating point는 총 8비트로
소수를 표현하는 방식인데
부호를 표현하는 s는 반드시 있어야 하는 것이고
exp는 4비트, frac을 3비트로 표현한다
앞에서 본 표준 IEEE format은 동일하고
denorm, norm format도 동일하지만
그냥 비트 수만 달라진 것이다
그렇다면 각각 exp과 frac의 비트수는 어떻게 영향을 줄까?
exp를 늘리는 것은 표현할 수 있는 값의 범위를 늘릴 수 있고
frac을 늘리는 것은 값의 정밀도를 늘릴 수 있다
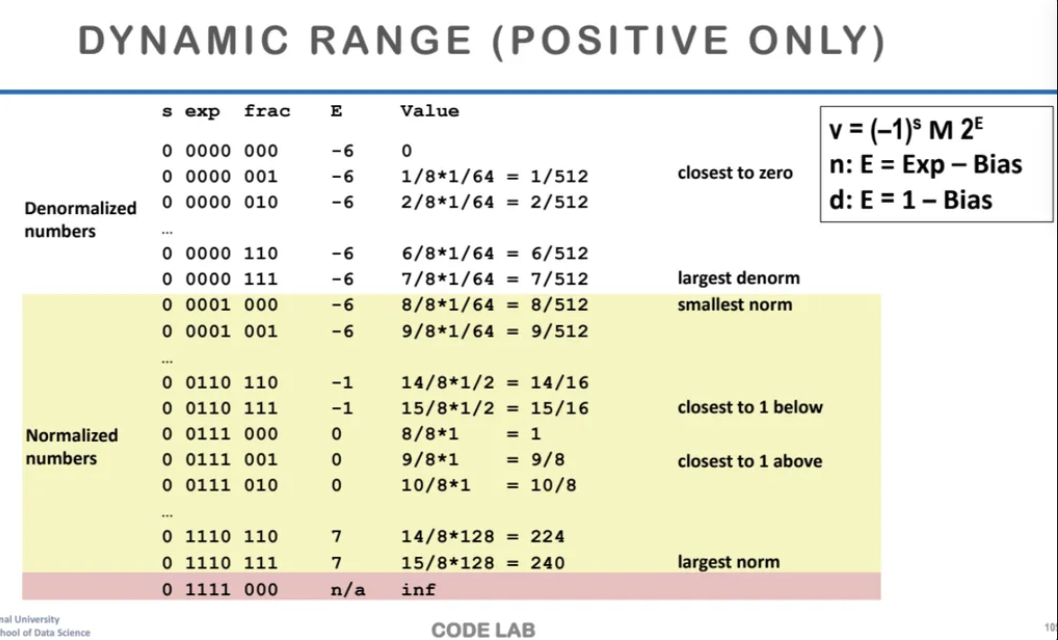
양수 범위에서 수의 범위를 알아보자
가장 큰 denorm은 exp가 전부 0인 값이고
frac이 전부 1인 값이다
그래서 0 0000 111이 가장 큰 denorm 값이 되고
여기서 denorm 값 범위의 마지막이 된다
그 다음부터는 exp에 0이 아닌 값이 나오게 되고
0 0001 000이 norm 범위의 가장 작은 값이 된다
이런식으로 쭈우우욱 가다가
exp가 전부 1111이 되면 infinity한 값이 된다
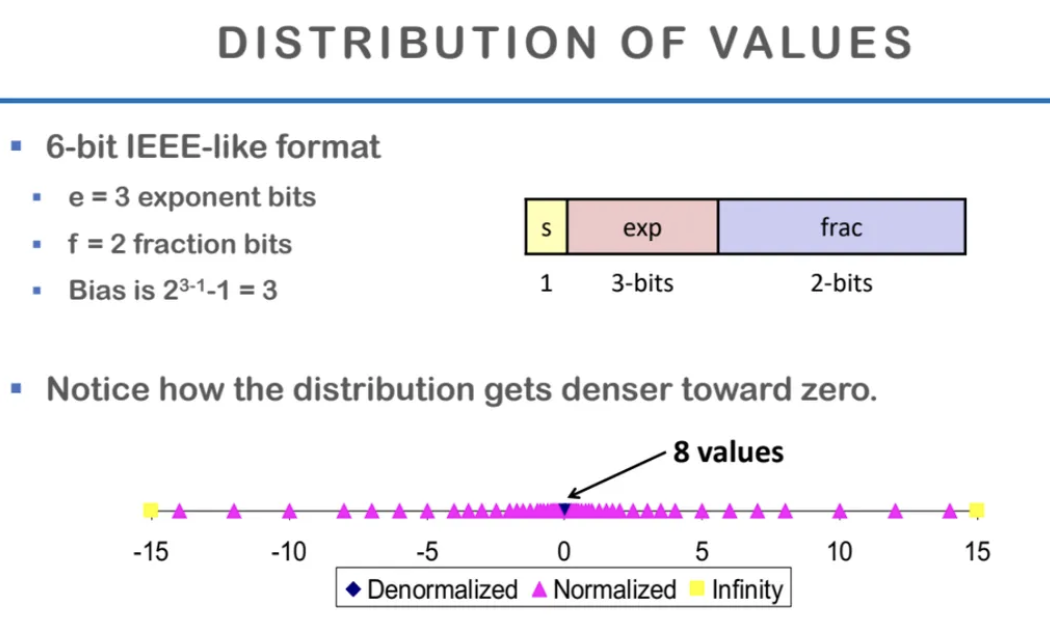
값들의 분포를 시각화 한 걸 살펴보자
그래프 가운데에 조그마한 파란색이 denorm으로
표현할 수 있는 값이다
0에 가까워질수록 점점 더 dense하게 표현이 가능하고
0에서 멀어질수록 점점 거리가 더 멀어진다
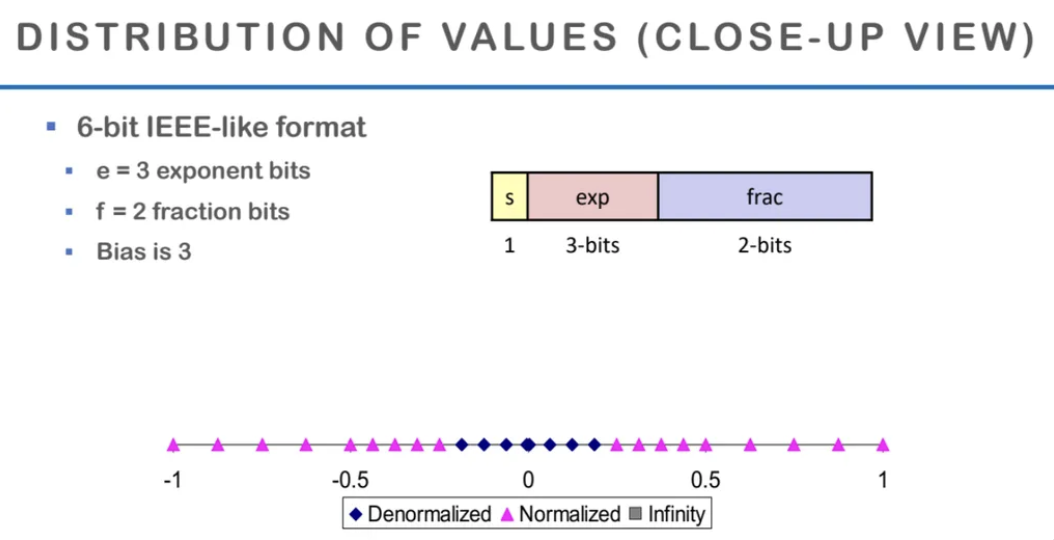
위에서 본 그래프를 좀 더 작은 부분으로 확대한 것이다
denorm으로 표현한 파란색 값의 범위가 보이고
denorm의 range가 끝나면
normalized의 range가 퍼져나가면서 표현된다

지금까지 배운 IEEE encoding 법 중에서
몇 가지 특별한 특징을 다시 상기시켜보자
위에서 확인했겠지만
exp의 값은 unsigned value처럼 표현한다
이렇게 bias를 넣어 양수로 표현하는 이유는
값의 비교를 쉽게하기 위함이었다
그래서 값의 비교는 unsigned integer의 비교와 비슷하다
그리고 integer와 다른 점인
+0, -0 모두 있다는 점을 기억해줘야한다

이제 간단하게 floating point를 활용한
몇 가지 연산을 좀 살펴보자
가장 처음은 round이다
round는 어떻게 표현할까?
그냥 하면 된다고 한다..
우리가 원하는 precxision으로
먼저 round 연산을 똑같이 해준다
만약 너무 exp가 크면
overflow가 될 수도 있다
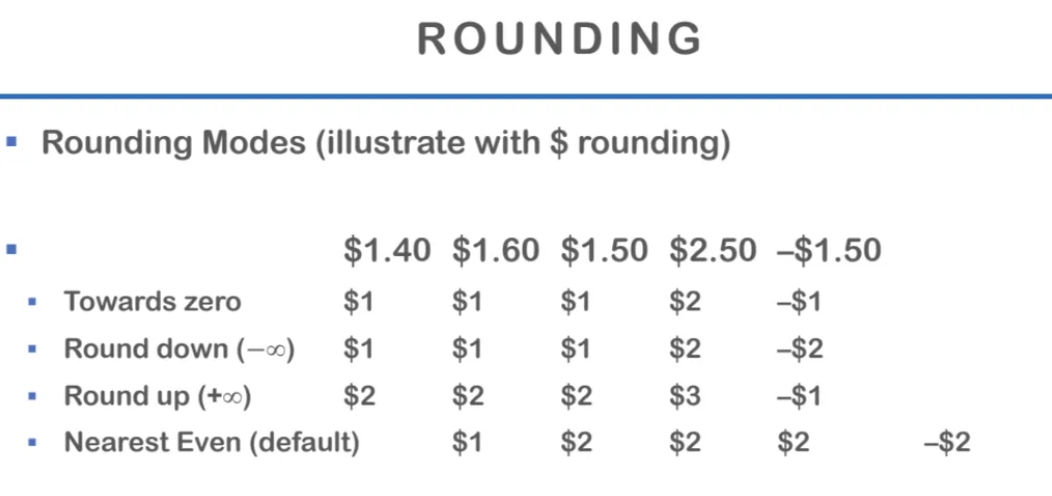
rounding을 한 값이다
(위 표에서 가장 아래 row는 한 칸 밀린거..)
우리가 알고있는 일반적인 round와 다르지않다

floating point 곱하기에 대해 알아보자
mantissa 부분은 실제 값을 표현하는 부분이기 때문에
그냥 곱하기를 해준다
부호는 XOR 연산을 통해 해주는데
부호가 같으면 양수, 다르면 음수가 된다
exponent를 곱하는 것은 지수 더하기와 같다
그래서 위 ppt의 Exact Result 처럼 결과가 나온다
그리고 Matissa가 2 이상이 된다면
지수로 넘겨줘야한다
지원할 수 있는 bit의 범위를 초과하면
overflow가 된다
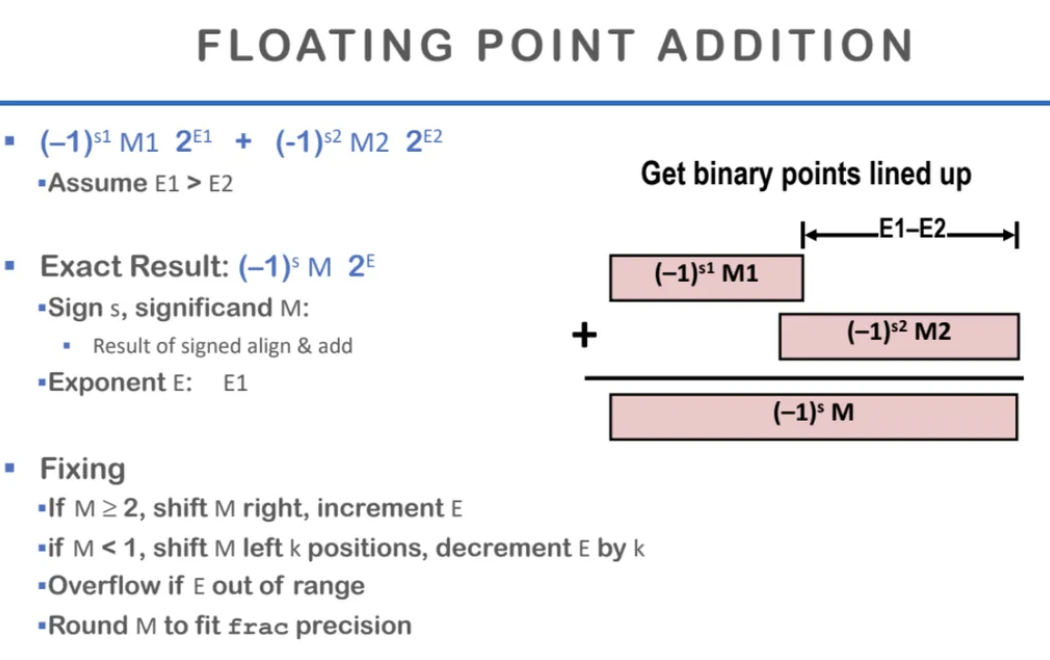
floating point의 더하기이다
matissa를 더해주면 된다
위 ppt처럼 더해주는 경우가 있다면
exp는 E1으로 통일한다
아까 곱하기 연산과 같이 2보다 커지면
right shift를 해주고
1보다 작아지면 left shift를 해줘서
E를 k만큼 줄인다고 한다

c언어에서 floating point가 어떻게 작동하는지 살펴보자
type casting에 관한 내용이다
floating에서 int로 casting하면
소수점 이하를 날리게 된다
이 때 floating point가 너무 크면 casting error가 뜬다고 한다
int를 float으로 보내면
정수부는 그대로 보내소 소수점 이하만 0으로 표현한다
보통 컴퓨터의 모든 연산에서
작은 범위에서 큰 범위로 가는 것은 대부분 안전하다
왜냐면 정보의 손실이 발생하지 않기 때문이다
따라서 int를 float으로 변환하는 것이
float을 int로 변환하는 것보다 안전한 연산이다

c언어에서 type casting을 하는 방법이다
다 해보면 알겠지만 그냥 저런식으로 할 수 있다
아무리 이렇게 casting을 할 수 있다고 해도
내가 표현하고 싶은 수가
내가 casting하고 싶은 type의 범위 내에서
표현할 수 있는지 반드시 확인해야한다
지금까지 Bit Type과 Data 파트에서
integer, float에 대해서 자세하게 살펴봤다
이 두가지를 구체적으로 살펴본 이유는
integer와 float이 하드웨어가 지원하는
기본적인 타입이기 때문이다
그 이상은 하드웨어가 지원하지 않는다
왜냐하면 하드웨어는 0과 1만 인식하기 때문이다
나머지 char, struct와 같은 데이터 타입은
결국 이 Integer와 float을
소프트웨어적으로 조화해서 만든 고차원의 데이터 타입이다
아무튼 여기서 비트표현과 데이터타입 부분의 수업은 끝..!
다음 시간에는 메모리 계층구조에 대해서 배운다고 한다