이 게시글은
서울대학교 데이터사이언스대학원
조요한 교수님의
데이터사이언스 응용을 위한 컴퓨팅 강의를
학습을 위해 재구성하였습니다.
Tree란?
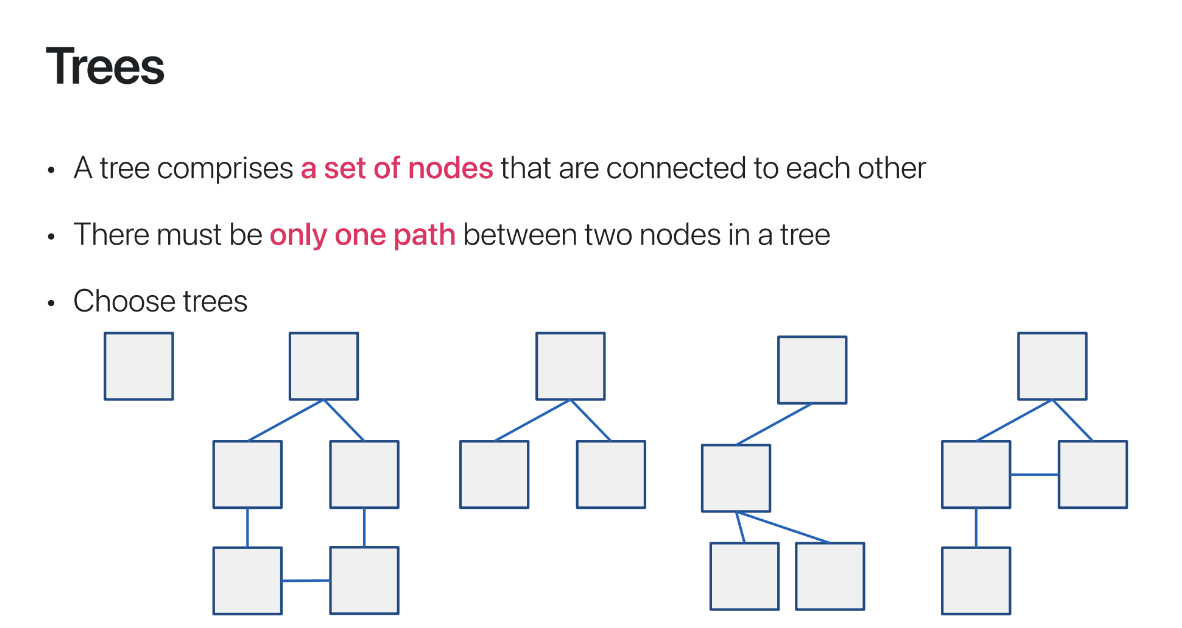
자료구조 중에서 Tree(트리)라는 친구가 있다
단순하게 말하면 트리는 서로 연결되어있는
노드들의 집합인데
노드와 노드 사이에는 반드시 한 개의 길만 존재해야한다
따라서 위 그림에서 Tree로 분류할 수 있는 것은
1번, 3번, 4번이라고 할 수 있다
이런 형태의 자료구조를 트리라고 부른 이유는
자료구조의 형태가 나무를 거꾸로 한 형태를 닮았기 때문인데
가장 출발점이 되는 노드를 root(뿌리)로 부르고
길을 통해 퍼져나가는 노드들의 모양이 leaf(잎)의
형태를 닮았기 때문이다
Rooted Binary Tree

Rooted Binary Tree는
Binary라는 뜻에서 유추할 수 있듯이
각각의 노드가 최대 2개까지 자식 노드를
가질 수 있는 노드를 뜻한다
하나의 node를 root노드로 설정한 뒤(그림의 경우 A노드)
자식 노드들을 최대 2개까지 연결해나간다
root 노드를 제외한 모든 노드들은
이전 노드인 부모(parent)노드가 반드시 존재해야하며
더 이상 자식 노드가 없는 노드들을 leaf노드라고 부른다
(그림의 경우 C, D노드)
Binary Search Tree

가장 중요한 Binary Search Tree(이진탐색트리)
옛날에 회사다닐 때 이진탐색으로 지겹도록
구현한 기억이 나서 더욱 반가웠었다
이진탐색트리란 Rooted Binary Tree와 같이
각 노드 당 최대 2개의 자식 노드를 가지는데
이 자식 노드들의 순서가 정해져있다
어떤 노드에 x라는 value가 저장되어 있다면
x노드의 왼쪽 자식 노드는 x보다 무조건 그 값이 작아야하며
x노드의 오른쪽 자식 노드는 x보다 무조건 그 값이 커야한다
그리고 이러한 조건이 모든 노드에 대하여 적용되어야한다
위의 그림으로 예를 들면
root노드의 값이 4이면
자식 노드 뿐만 아니라
root노드의 왼쪽에 있는 모든 노드들은
4보다 작아야 하며
오른쪽에 있는 모든 노드들은 4보다 커야한다
따라서 위 그림에서는 왼쪽의 노드들은
4보다 작은 2, 1, 3의 값이
오른쪽의 노드들에는
4보다 큰 6, 5, 7의 값이 저장되어있는 것을 확인할 수 있다
모든 노드들에 대해서 이러한 조건들이 지켜져야하며
모든 노드들의 값은 unique해야한다
(같은 값을 가지는 노드가 존재하면 안된다)
이런 특징을 가진 트리가 어떻게 쓰이며 왜 중요하냐면
Tree에 이름에서 알 수 있듯이
Search(탐색)을 할 때 시간을 굉장히 줄일 수 있다
예를 들어 내가 7이라는 값을 찾고싶다면
위 그림에서는 root노드가 4니까
찾고하자는 7이라는 값이 4보다 크므로
오른쪽으로 들어가고
그다음 나온 6이라는 노드는 또 7보다 작으니까
6 노드의 오른쪽으로 진입하면
7을 손쉽게 찾을 수 있다
K-ary Tree

바이너리 트리의 확장된 버전의 트리이다
자식 노드가 2개만 가질 수 있었던 바이너리 트리와 달리
자식 노드를 여러 개 가질 수 있다
위는 K-ary Tree를 파이썬 코드로 구현한 예시인데
위에서 arity는 한 노드가 최대 몇 개의 자식을
가질 수 있는지를 나타낸다
위 코드에서는 각각의 child는 list형태로 존재하며
arity의 값인 최대 k개만큼 존재 할 수 있다
Graph
그래프와 트리는 사실상 비슷한 부분이 많은데
이는 트리가 그래프의 일부이기 때문이다
Tree는 그래프의 한 형태이고
그래프는 트리보다 좀 더 큰 범주라고 생각하면 된다
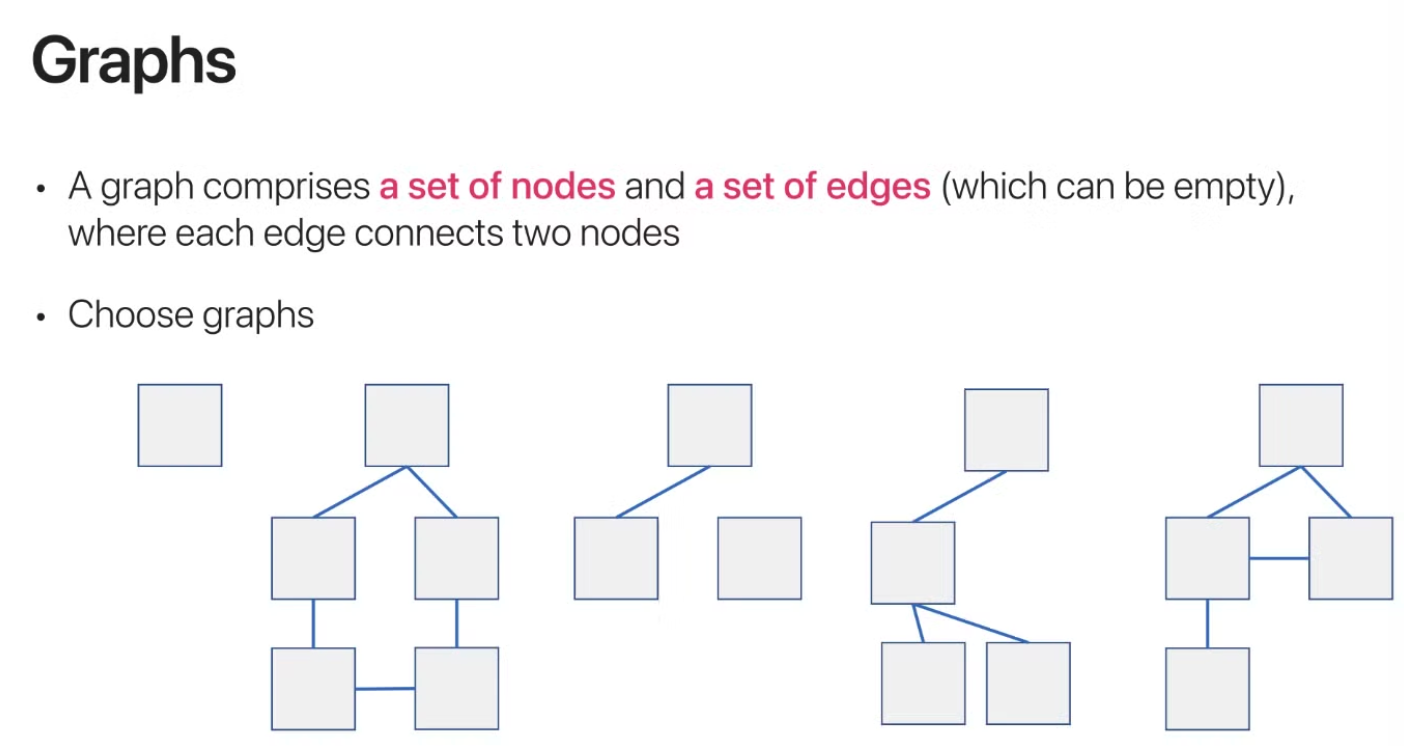
그래프는 노드들과 엣지들의 집합인데
노드는 위 그림에서 사각형 한 개를 뜻하고
엣지는 간선(vertex)로 두 노드를 연결해주는 선을 뜻한다
Graph에서 사용되는 용어를 정리해보면
정점을 vertex라고 하고
node(v)와 같은 방식으로 표기한다
간선을 Egde로 표기하고
두 vertext v와 w를 연결해주는 edge를
connection(v, w)로 표기한다
그리고 두 vertex가 egde로 연결되어있을 때
둘은 adjacent하다고 표현한다
path(경로)는 결국 vertex들의 sequence로
edge로 연결된 vertex들의 시퀀스를 뜻한다
simple graph와 simple path가 있는데
simple graph는
loop(반복)을 갖고있지않고
parallel edge도 갖고있지않은 그래프를 뜻하고
simple path는
unique한 vertex들로만 구성된
한 마디로 동일한 vertex가 두 번 이상 나타나지않는
path를 뜻한다
graph에서의 cycle은
첫번째 vertex와 마지막 vertex가 동일한 것을 말하며
이러한 cycle이 한개라도 존재하는 그래프를 cyclic graph
한 개의 cycle도 존재하지 않는 그래프를 acyclic graph라고 한다
graph가 connected 하다는 말은
모든 vertex들이 연결되어 있는 graph를 뜻하고
그렇지 않은 graph는 disconnected graph라고 부른다
edge가 방향을 갖고있는 그래프를 directed graph
그렇지 않은 graph는 undirected graph이다

따라서 사진과 같은 지하철 노선도는
지하철역이 vertex
역과 역 사이를 이어주는 노선이 egde인 그래프이다
모든 지하철역들이 다 이어져있으므로
connected하며
2호선의 경우 순환선이므로 cyclic
양방향 모두 다녀갈 수 있는(방향이 없는) undirected한 그래프이다

그래프를 파이썬으로 구현하면 다음과 같이 구현할 수 있다
vertex와 egde의 리스트를 넣어주고
edge는 dictonary 형태로 구현해 줄 수 있다
'강의 > computer programming' 카테고리의 다른 글
| [ComputerScience] C++과 Namespace (1) | 2024.09.20 |
|---|---|
| [ComputerScience] 알고리즘의 시간복잡도와 탐색, 정렬 (Binary Search, 깊이우선탐색, 넓이우선탐색, Selection Sort, QuickSort, Merge Sort) (3) | 2024.09.19 |
| [computerScience] Array, Linked List, Queue, Stack, Hash Table (1) | 2024.09.13 |
| [ComputerScience] C언어와 포인터 (4) | 2024.09.09 |
| [ComputerScience] 프로그래밍 언어 개요(python의 Module과 Class, 객체지향(OOP)의 4가지 원칙) (3) | 2024.09.06 |