본 게시글은 Stanford 대학교 Jure Leskovec 교수님의
Stanford CS224W: Machine Learning with Graphs(2021) 강의를 듣고
학습을 목적으로 재구성한 글입니다
스스로 정리한 내용이라 오류가 있을 수 있습니다
https://web.stanford.edu/class/cs224w/
CS224W | Home
Content What is this course about? Complex data can be represented as a graph of relationships between objects. Such networks are a fundamental tool for modeling social, technological, and biological systems. This course focuses on the computational, algor
web.stanford.edu
https://www.youtube.com/watch?v=6g9vtxUmfwM&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=15
이제 GNN Framework 파트는 전반적으로 벗어나서
Graph 구조와 embedding을 활용하는 파트에 대한 설명으로 넘어왔다
그 시간 중 첫 번째는 바로 Knowledge Graph(KG)
우리 연구실에서 하는 프로젝트와도
깊은 관련이 있어서 열심히 들었던 것 같다

오늘 내용은
knowledge graphs completion with embeddings

그렇다면 우선 Knowledge Graph(KG)란 무엇일까
KG는 node(entity), edge(relationship)가 존재하고
각 node와 edge마다 각각의 type들이 존재하는 구조이다
KG는 우리가 앞에서 배운 heterogeneous graph의
대표적인 예시라고 할 수 있다
KG는 이름과 비슷하게 여러 분야의 지식을
그래프 구조로 표현한 것을 말한다
여러 지식들이 그래프 구조로 연결되어있으면
그래프 구조를 타면서 지식 추론이 가능해지기때문에
KG는 많이 연구가 되고 있는 분야이다
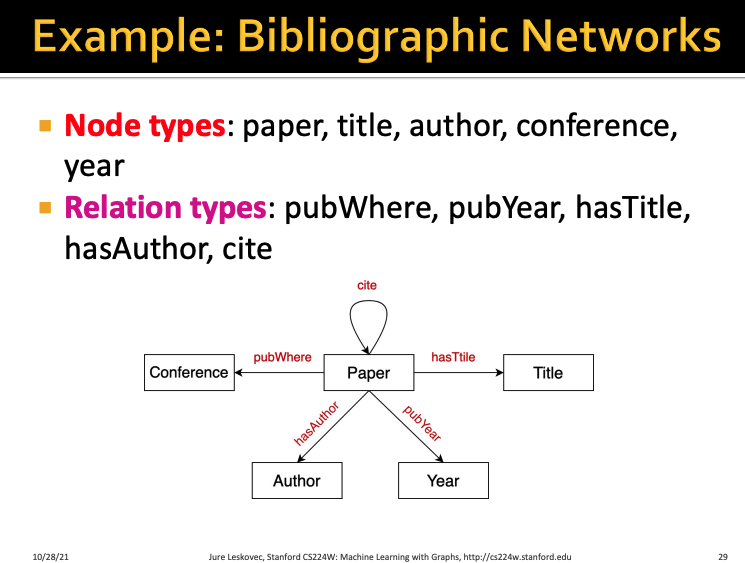
KG의 예시 중 1개이다
어떤 논문의 정보를 위와 같이 그래프 구조로 표현할 수 있다

두 번째 KG의 예시이다
bio 분야에서의 지식을 그래프 구조로 나타낸 KG이다
각각의 relationship은 has_func, causes, assoc, treats 등이 있다

실제로 이런 곳들에서 Knowledge Graph를 쓰고있다고 한다

흔히 우리가 사용하는 wikipidea를 생각해보자
내가 어떤 지식이 궁금해서 wikipidea page에 들어가서
해당 문서를 확인했다
그때 우리가 해당 위키 페이지에서 글을 읽다보면
다른 위키 페이지로 하이퍼링크를 타고 가면서
관련 문서들로 계속 타고 타고 갈 수 있다
이게 바로 KG의 대표적인 구조이다
따라서 이런 KG 구조를 이용해서
자연어 question이 들어오면 이를 처리하고
KG 구조를 바탕으로 답을 찾아내서 답변을 해주는
Question Answering System도
KG를 활용하는 대표적인 사례 중 하나이다

따라서 이러한 질의응답을 위해서는
KG는 굉장히 거대하고 다양한 지식을 갖고 있어야하는데
지식구조라는 것이 당연히 그렇듯
너무 거대하기 때문에 그 안에서 관계들이 빠져있을 수가 있다
따라서 우리가 지금 해결하고 싶은 것은
KG에서 빠져있는 관계들을 우리가 완성할 수 있을까? 이다

대표적인 KG 중 1개인 Freebase이다
freebase에는 8천만개정도의 엔티티가 존재하고
38000개 정도의 relation type이 존재하는데
Freebase에 존재하는 person 중에서
태어난 장소가 빠져있는 비율이 78.5%라고 한다
이처럼 거대한 KG일지라도 그 안에서
빠져있는 정보가 많고 우리는 이걸 채우고 싶은 것이다

각각의 방법들에 대해 차근차근 알아보자
빠진 relationship에 대해서 우리가 complete하는 방법들이다
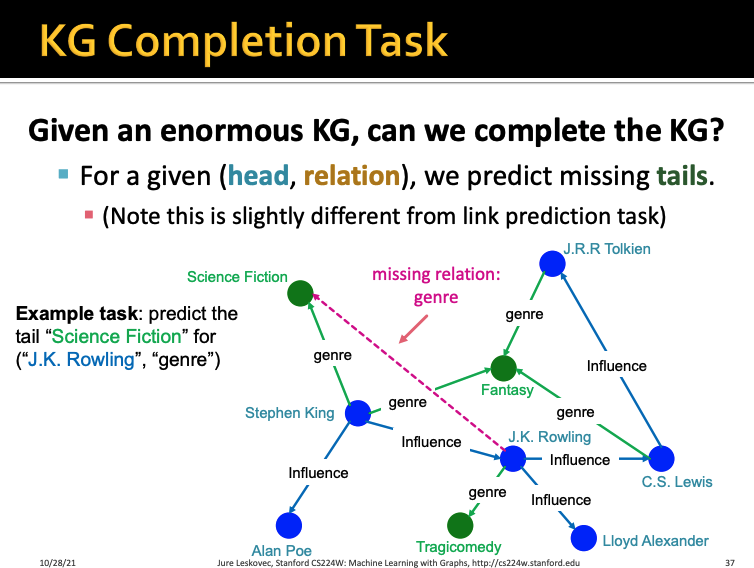
위와 같이 거대한 KG가 주어졌다고 했을 때
우리는 빠진 관계가 있으면 이를 완성시켜야한다
이는 우리가 이전까지 배웠던 link prediction이랑은 결이 조금 다르다
위 예시를 한 번 살펴보자
J.K. Rowling이라는 노드와 Science Fiction이라는 노드가 있으면
이 둘 사이의 relation type은 genre라는 것을 예측할 수 있어야한다

그렇다면 이 KG를 수학적으로 어떻게 표현하는지부터 알아보자
KG에서 node와 node별 edge는 triple이라는 (h, r, t)구조로 표현된다
h는 head, r은 relation, t는 tail이다
이 각 엔티티와 관계들을 d차원의 벡터로 표현해서
vector space에 넣어야한다
이건 이전에 배운 shallow embedding 같은 방식으로 넣을 수 있고
GNN과는 상관이 없는 내용임을 기억하자
따라서 우리가 하고싶은 것은 triple (h,r,t)가 주어졌을 때
(h, r)의 embedding이 t의 embedding과
가까이 위치하도록 embedding을 시켜줘야하는 것이다
따라서 이걸 위해서 2가지를 고려해야한다
1. (h, r)을 어떻게 임베딩할까?
2. 어떤게 가까운 것일까?

우선 이를 수행하는 첫 번째 방법인
TransE부터 살펴보자
TransE의 가장 Key idea는
같은 embedding space에 있는 h, r, t에서
h+r = t가 되어야한다는 것이다
즉, 벡터 h에서 벡터 r만큼 평행이동을 하면
벡터 t에 도달해야한다는 것이다
따라서 이를 식으로 나타내면

이렇게 되는데
h+r한게 t에 가깝게 embedding 될 수록 좋다는 뜻이고
따라서 h+r-t를 한게 0에 가까워질수록 좋다는 뜻이다
즉, 작을수록 좋은 것이라서 절댓값 앞에 음수를 붙여줬다

TransE를 학습시키는 알고리즘은 위와 같다고 한다
한 번 간단하게 살펴보면 좋을 것 같다

그렇다면 KG에 있는 triple들 중에서
분명히 어떤 패턴을 갖고 있는 것들이 있을 것이다
위 ppt slide에서 예를 들면
h는 t의 roommate라면
t도 h의 roommate 관계가 될 수 있다
이는 symmetry(대칭) 관계라고 볼 수 있다
그 다음 h가 t의 advisor라면
t는 h의 advisee가 된다
이렇게 inverse(반대)의 관계를 가질 수도 있다
그렇다면 TransE는 이러한 triple relation의 패턴들을
충분히 표현할 수 있을까?

relation의 Pattern은 이렇게 크게 4가지로 구분할 수 있다
첫 번째는 우리가 위에서 살펴본 h, t의 관계와 t, h의 관계가 같은 것과(symmetric)
h, t의 관계와 t, h의 관계가 반드시 달라야하는 것을 뜻한다(antisymmetric)
두 번째는 h, t와 t, h의 관계가 반대인 것을 의미한다
세 번째는 x와 y의 관계가 r1이고 y와 z의 관계가 r2라면
x와 z의 관계는 r3인 것을 말한다
마지막으로 1-to-N은 t1부터 tn까지의 모든 t들은
h와 동일한 관계를 갖고 있는 것을 말한다

그렇다면 위에서 본 각 패턴들을
TransE가 제대로 표현할 수 있는지를 살펴보자
우선 antisymmetric 같은 경우는
h+r = t가 나올 때
t+r의 결과가 t가 나오지 않으면 성립하는 것이 된다
이건 위와 같이 표현할 수 있으므로
TransE에서 antisymmetric은 표현할 수 있는 패턴이 된다

이제 inverse relation을 한 번 살펴보자
h+r1이 t라면 t+r2을 했을 때 다시 t가 나와야한다
즉, r1 = -r2가 되어야하는 것이다
즉 위와 같은 관계가 되면 되는 것이므로
TransE로 inverse relation도 표현이 가능해진다

그렇다면 composition 관계는 어떨까?
composition 관계를 TransE로 표현하기 위해서는
r1 + r2가 r3가 되면 된다
즉 위 ppt처럼 나오면 되는 것이므로
TransE로 composition relation도 표현이 가능해진다

하지만 symmetric relation은?
h + r 을 해도 t가 나와야하고
t + r을 해도 h가 나와야하는데
이렇게 되려면 r이 0이고 h=t인 경우만 가능하다
하지만 h와 t는 절대 같을 수가 없으므로 사실상 불가능 한 것이다
따라서 TransE로 symmetric relation은 표현이 불가능한 것이다

그럼 마지막으로 1-to-N relation을 살펴보자
결론부터 얘기하면 TransE는 1-to-N relation을 표현하지 못한다
왜냐하면 1-to-N relation이 성립하려면
h+r=t1=t2=t3 ... =tn이 되어야하는데
t1과 t2가 같을 수가 있을까?
각 n개의 t들은 모두 다른 엔티티이기 때문에 달라야만한다
하지만 TransE로는 이걸 표현할 수가 없는 것이다

그렇다면 다른 방법인 TransR을 살펴보자
TransE는 우리가 엔티티와 관계를 모두 같은 embedding space에 놓았다
하지만 본질적으로 entity와 relation은 같지가 않기 때문에
entity와 relation이 다른 embeddign space에 있게끔 하는 것이다
그게 바로 TransR의 key point이다

따라서 entity는 k차원의 entity space에 넣고
relation은 d차원의 relation space에 넣어준다
그런 다음 관계 r에 대해서 r*d차원의 Mr으로 projection 시킨다
따라서 h를 Mr으로 투영시킨 값과
t를 M으로 투영시킨 값을 활용해서
score function을

위와 같이 계산할 수 있다

그렇다면 이 TransR로 아까 봤던 각각의 relation pattern들을
어떻게 설명할 수 있을지 살펴보자
우선 symmetric부터 살펴보자
TransR에서 symmetric은 투영시키는 벡터값인 Mr을
각각 t와 h에 적용해주었을 때 그 결과가 같으면 된다
따라서 위 ppt slide처럼 표현할 수 있고
TransR에서 symmetric은 표현할 수 있는 것이다

antisymmetric 관계도 한 번 살펴보자
이것도 이전의 TransE와 유사하게
t와 h에서 Mr을 투영시킨다음 r을 더한 값이 t를 투영시킨값과 같아야하고
그 t를 투영시킨 값에서 r을 더한게 h를 투영시킨값과 같으면 안된다
따라서 위 ppt slide처럼 표현할 수 있으므로
TransR에서 antisymmetric relation은 표현할 수 있다

그렇다면 이제는 1-to-N 관계를 살펴보자
1-to-N relation은 t1부터 tn까지의 값을 Mr로 투영시켰을 때
h를 투영시켜 r을 더한값과 모두 같아지게하면 된다
따라서 TransR은 1-to-N relation도 표현할 수 있다

그다음 inverse relation도 한 번 살펴보자
각각 t와 h를 relation space로 투영시킨 값들이
r1 = -r2면 inverse relation도 표현할 수 있게된다
따라서 TransR은 inverse relation까지 표현할 수 있는 것이다

마지막으로 composition relation을 한 번 살펴보자
내가 들은 강의의 버전에서는
TransR은 각 relation들이 모두 다른 공간에 위치하고 있기 때문에
모델링이 불가능하다고 했었는데 ;; ㅋㅋㅋ
ppt의 버전에서는 모델링이 가능하다고 한다
이후에 연구가 계속 진행되면서
TransR에서도 composition relation을 모델링하는 방법이
연구가 된 듯 하다

강의로 내용을 듣지 못해서 정확하게 어떻게 모델링되는지는 모르겠지만
각각 다른 공간에 있는 r들이 어떻게 연결이 되나보다

그렇다면 이제 DistMult에 대해서 알아보자

우리가 지금까지 앞에서 본 TransR과 TransE는 그냥 벡터간 거리인
L1/L2 distance의 negative 값을
score function으로 사용했다
하지만 DistMult 방식은 k차원의 벡터 공간에
entitiy와 relation들을 모두 embedding 시킨다

이러한 DistMult의 score function은 세 백터를 곱한 것의 합으로 나타내는데
이는 cosine similarity와 유사한 방식이다
즉, t가 h*r의 방향에 얼마나 잘 정렬되어있는지를 보는 것이다
이제 이걸 바탕으로 각 relation pattern들을 잠깐 살펴보자

각 t들이 h*r과 유사한 방향에 존재하면 되므로
DistMult로 1-to-N을 표현할 수 있다

symmetric 역시 당연하게 DistMult로 표현할 수 있다

하지만 antisymmetric은 표현할 수 없다
이것도 당연한것이 symmetric이 반드시 성립하게 되어있기 때문에
자연스럽게 antisymmetric은 성립할 수가 없는 것이다

또한 inverse relation도 DistMult가 표현할 수 없다
왜냐하면 inverse는 r1과 r2를 각각 적용한 score이 같아야하는데
이게 되려면 r2와 r1은 같아야하고
r2와 r1은 같을 수가 없기 때문이다

마지막으로 composition relation도 표현할 수가 없다
그 이유는 DistMult는 결국 h와 r에 대해서 hyperplane을 정의하는 방식이다
그런데 composition 관계는 여러 개의 관계가 나오게 되는데
이를 하나의 hyperplane으로 표현할 수가 없기 때문이다

마지막으로 ComplEX를 살펴보자

우리가 지금까지는 각각의 벡터들을
일반적인 vector space에 embedding 시켰다면
ComplEX는 복소수 벡터공간(각 차원의 값이 허수)에
엔티티와 관계를 embedding 시킨 것이라고 한다
위 ppt slide에서 세로축은 실수부이고
가로축은 복소수 전체 값을 나타낸다

ComplEX도 DistMult에 기반해서 entity와 relation들을
복소수 space에 embedding을 시킨다
그런 다음 score function을 계산하는데
거기서 실수부만 추출을 한다

ComplEX에 대해서 강의에서 깊게는 다루고 있지 않다
우선 ComplEX로 Antisymmetric relation은 표현할 수 있다
이게 DistMult와 사실상 score function이 동일한데
어떻게해서 같을 수 있냐 싶겠지만
복소수 공간을 사용하기 때문에 가능하다고 한다
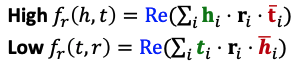
각각의 값들을 최대한 높은건 높게
낮은건 낮게 학습시키는 것이 좋다고 한다

아무튼 ComplEX는 DistMult와 유사하기 때문에
3개의 내적은 다 동일한 값이라서
symmetric은 당연히 성립한다

inverse relation도 표현할 수 있지만

composition은 표현 X
1-to-N은 표현이 또 가능하다고 한다
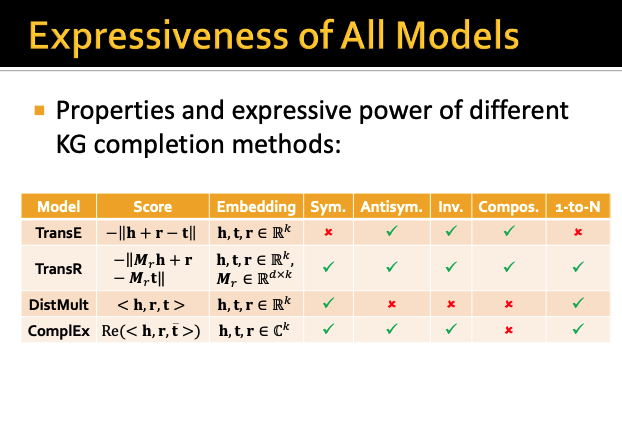
이번시간에 배운 KG completion methods들을
각 relation pattern별로 정리해보면 위와 같다
'강의 > graph neural network' 카테고리의 다른 글
| [GNN] Heterogeneous Graphs (RGCN) (0) | 2025.09.17 |
|---|---|
| [GNN] How Expressive are Graph Neural Network? (GIN model) (0) | 2025.09.08 |
| [GNN/Colab 실습] PyTorch Geometric(PyG)로 GNN 구현하기 with OGB dataset (3) | 2025.09.03 |
| [GNN] Graph Training (Stacking Layers Problems, Prediction Head, Loss, Evaluation) (0) | 2025.09.03 |
| [GNN] A General Perspective on Graph Neural Networks (GCN, GraphSAGE, GAT) (1) | 2025.09.01 |