본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다
본격적으로 머신러닝 내용을 시작한다
그 첫번째 주제는 바로 linear regression
교수님의 말씀 한마디 한마디 전부다
최대한 설명에 담아보려고 애썼다
그렇다면 .. 시작-!
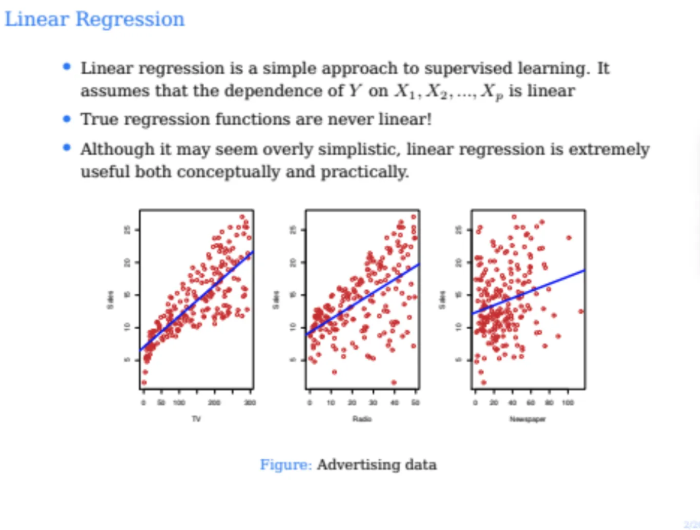
linear regression은 지도학습과 비지도학습을 얘기하는데 있어서
가장 기초가 되는 개념이다
지도학습에서는 x와 y가 있고
그 x는 feature, y는 response variable이라고 부르는데
결국 x와 y가 어떠한 correlation이 있다면 거기에서의 선형관계를 찾아내는 것이다
여러 데이터들 속에서 선형관계를 찾아내는 것이 linear regression이라고 했는데
그렇다면 .. 과연 모든 데이터가 선형관계에 있을 수가 있을까?
즉, 어떤 true regression function이 정말로 truly linear일 수가 있을까?
사실 있을 수는 있다
여기서 말하는 선형관계라는 것은
데이터가 무조건 선 안에 있어야한다는 것이 아니다
데이터의 전반적인 분포가 선형적으로 되어있다는 뜻이다
따라서 데이터의 관계가 truly linear하지 않을 수는 있지만
이런 linear regression은 이미 여러 분야에서 사용되고 있다
또한 이러한 linear regression은 조금 더 복잡한 함수들을
이해하는데에 있어서 중요한 step이 된다

이전 slide에서 나왔던 그래프들은 이전 수업에서도 다뤘던
광고매체별 광고비와 sales의 상관관계를 나타낸
linear regression의 예시이다
그럼 위 예시를 보고 우리는 다양한 질문들을 던질 수 있다
예를 들면
advertising budget이랑 매출들이 얼마나 관계가 있는지
그리고 그 관계가 얼마나 강한지
그리고 각각 어떻게 영향을 미치는지
등과 같은 질문들을 할 수 있다
simple linear regression

처음으로 input이 1개인 single predictor
즉, single linear regression에 대해서 배워보자
우선 single predictor에서의 linear regression을 공부하면
이걸 여러 개의 feature를 가진 multiple linear regression으로 확장하는 것은 아주 쉽다
linear model인 true model은

이렇게 작성할 수 있다
위에서 X는 feature가 1개만 존재하고
feature가 1개인 X에는 B1이라는 파라미터(coefficient)가 있다
위 식만 보면 저 친구는 1차함수니까 그냥 선 모양이다
거기에다가 입실론이라는 노이즈 값이 존재하는 형태이다
이렇게 생긴 linear model을 single linear regression이라고 한다
위 식을 보면 predictor X는 1개지만
파라미터 B는 B0, B1 이렇게 2개가 있다
중학교 때 배우는 일차함수를 생각하면
B0은 y절편(intercept), B1은 함수의 기울기(slope)가 된다
우리가 이전 시간에도 굉장히 강조했던 내용인데
입실론은 평균이 0이고 x와 독립적인 노이즈값이다
우리의 목표는 B0과 B1을 학습시키는 것이다
그래서 B0과 B1에 대한 estimate를 구하는데
이 estimate를 B0^, B1^으로 표현한다
특정 x를 받았을 때 이 특정 x에 대한 prediction은 우리가 구한
B의 estimate를 기준으로 구하면 되고
그렇게 나온 결과값이 y^이 된다

우리가 가진 datapoint(x, y쌍)가 총 N개가 있다고 가정해보자
i번째 datapoint에서 i번째 y의 값을 알 수 있다
그리고 B0^, B1^을 알고 있다면 우리는 예측값 y^도 구할 수 있다
그런데 i번쨰 y값인 yi는 실제로 있는 값, 즉 정답이 된다
따라서 우리의 예측값 y^이 예측이 잘 된 값인지를 비교하려면
정답 yi와 비교하면 된다
따라서
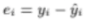
두 값의 차이를 구해서 저게 작아지도록 만들어주는데
이때 두 값의 차이를 residual이라고 부른다
하지만 차이라고 하는 것은 양수나 음수가 될 수 있기 때문에
이 값의 절댓값이 작아야되는 것이다
그래서 그냥 제곱을 해버린다
아까 datapoint, 즉 observation이 n개가 있다고 했다
그러니까 n번째 까지의 residual 값들을 다 square한 다음 더한다
이렇게 구해진 값을 RSS(Residual Sum of Squares)라고 부르는데
따라서 우리는 이 RSS를 최소화시키면 된다

이 RSS를 가장 작게 만드는 B0^과 B1^을 찾으면 되는 것이다
우선 정답부터 보자
이 RSS를 최소로 만드는 B0^과 B1^은
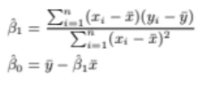
이렇게 된다
xbar, ybar는 각각의 평균값이다
B1^은 위의 linear에서 기울기의 값이었다
따라서 B1^을 위처럼 구하면 RSS를 minimize 시키는 기울기가 되는 것이고
B0^은 ybar와 xbar를 이용해서 만드는 intercept이다
이게 정답이긴한데
그렇다면 위 B1^, B0^ 값들을 어떻게 구했을까?

우리가 구해야하는 것은
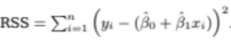
위 2차식인 RSS를 최소화하는 B0^, B1^의 값이다
2차식이기 때문에 간단하게 생각해봐도
미분을했을 때 0이 되는 값을 구하면 된다고 생각할 수 있다
우리가 알아야할 값은 2개지만
우선 1개를 기준으로 미분을 해보자
B0^을 기준으로 미분하고 나머지는 상수 취급하자
그렇게 B0^을 기준으로 미분하고 식을 정리하면
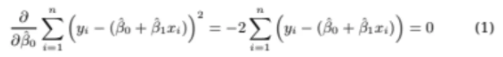
이렇게 된다
위 식을 0으로 만드는 B0^ 값을 구하면 되는 것이다
마찬가지로 B1^을 기준으로도 미분해보자
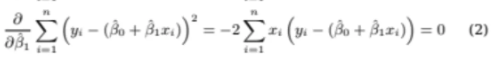
동일하게 위 식을 0으로 만드는
B1^의 값을 구하면 된다
그렇다면 우리가 구해야 하는 미지수 2개
우리가 알고있는 식도 2개니까
이건 연립방정식으로 뚝딱하면 구할 수 있는 것이다
따라서 위 식을 정리하면
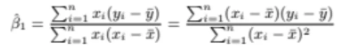
최종적으로 이렇게 나오는데
정리하는 과정이 크게 어렵지 않아서 한 번 정리해봤다

ㅎㅎ.. 아무튼 이렇게 식이 정리가 되어서
B0^과 B1^은 저렇게 값이 나오게 된다

위에서의 advertising data로 linear regression을 fit 시킨 모습이다
빨간 점이 실제 데이터들인데 검은 실선이 오차(residual)이다
저건 true function이 아니기 때문에 입실론값이 아니다
yi^는 blue line 위의 값이고
yi는 빨간점의 값이다
저 검은 실선(residual)들을 다 제곱해서 더한 것이 RSS이고
이걸 minimize하도록 B0과 B1을 학습시켜서 나온 선형 함수가 blue line이 된다
우리가 위 데이터를 육안으로 봤을 때 딱봐도
선형성이 강하다는 것을 느낄 수 있다
데이터들이 아무래도 TV에 광고료를 쓸 수록 매출이 올랐다고
우리가 판단할 수가 있을 것이다
하지만 이건 우리가 그냥 눈으로 봐서 대강 판단한 것이다
이게 1차원이라서 이렇게 시각적으로 확인할 수 있는 것이지
고차원 데이터로 가면 육안으로는 선형성 판단이 불가해진다
또한, 눈으로 보고 대충 어림짐작하는 것보다
어떤 수치를보고 이 데이터가 선형성이 강한지 아닌지를
판단하는 기준이 필요하다

이전 시간에 잠깐 얘기했는데
우리가 학습시키는 linear model도 결국 random variable이다
왜냐하면 학습시키는 데이터에 따라서
linear model이 달라지기 때문이다
파라미터들도 당연히 random variable이다
따라서 이러한 estimate에는 variance가 존재하고
베타값들에 대해서도 standard error가 존재한다
위 ppt는 이러한 standard error에 대한 설명이다

B1^의 standard error SE(B1^)은 위와 같이 나타낼 수 있다
분자에는 시그마 제곱이 들어가는데
시그마제곱은 입실론 값, 즉 절대 줄일 수 없는 값이다
분모는 xi와 x들의 평균들의 차의 제곱의 합이다
직관적으로 xi에서 x들이 얼마나 떨어져있는지에 대한 정도이고
이건 sample variance 값이다
한 마디로 x값들이 평균으로부터 넓게 퍼져있으면 분모가 커지고
SE의 값이 작아지게 된다
SE 값이 작다는 것은 기울기(B1^)가 안정되어있다는 의미이다
반대로 x들이 평균에 몰려있으면 분모가 작아지면서 SE의 값이 커지게 되고
이 말은 기울기(B1^)가 안정되지 않는다는 뜻이다
요약하면
입실론(노이즈)가 크면 기울기가 불안정해지는 것이고 (SE가 커지므로)
x들이 평균에 몰려있으면 기울기가 불안정해진다(SE가 커지므로)
그렇다면 B0^의 SE를 살펴보자

식이 조금은 더 복잡하지만 직관은 B1^과 비슷하다
결국 B0^도 x들이 평균으로부터 얼마나 떨어져있냐에 따라서
stable한지 안한지가 정해진다
stable하다는 것은 standard error가 작다는 뜻이고
이는 B0^값이 잘 바뀌지 않는다는 뜻이다
x들이 상당히 모여있으면 x가 조금만 바뀌어도
기울기가 급하게 바뀌게 된다
지금까지 B1^, B0^의 standard error 값에 대해서 알아보았는데
눈치챘을 수도 있겠지만 이 두개의 SE를 구할 때
x값만 있지 y값은 없다
SE를 구할 때는 x값이 평균으로부터 얼마나 떨어졌는지가 중요한 요소가 된다
그렇다면 이 SE 값을 어디에 쓰냐?
이 SE 값이 있으면 각각의 estimate에 대한 confidence interval(신뢰구간)을 구할 수 있다
즉, 불확실성의 범위를 알 수 있다는 뜻이다
보통 95% 신뢰구간을 구하기 위해서 정규분포 1.96을 사용해서
약 2배 정도로 계산해서 구한다

위 구간 안에 진짜 기울기의 값이 존재할 확률이 95%라는 뜻이다

그런데 이 신뢰구간에 대해서 잘못 해석하는 경우가 많다고 한다
즉, 그렇게 데이터 1개를 넣으면 1개의 신뢰 구간이 만들어지고
데이터 2개를 넣으면 2개의 신뢰 구간이 만들어지게되고
100개를 넣으면 100개의 신뢰구간이 만들어지게된다
그럼 이 100개 중에서 95개가 true Beta
즉, 진짜 B1값을 포함한다는 의미이다
나도 이게 무슨 말인지 잘 이해가 안되어서 gpt 칭구와 열심히 토론했는데
좀 더 쉬운 말로 정리하면 이렇다
위 예시를 통해서 살펴보자
B1의 신뢰구간이 [0.042, 0.053]이라고 했는데
이게 진짜 B1의 값이 0.042와 0.053의 사이에 있다는 뜻이 아니다
이 말은 여러 개의 데이터를 가지고
SE를 구하는 똑같은 공식을 갖고 신뢰구간을 계산했을 때
95%의 확률로 그 신뢰구간 안에 B1이 있다는 뜻이다
즉, 우리가 구해야하는 확률 변수가 B1의 값이 아니고
진짜 B1의 값이 지금 구한 신뢰구간 안에 있을 확률이다
아무튼 위 예시는 B1에 대한 신뢰구간이기 때문에
기울이게 대한 신뢰구간이다
따라서 우리는 TV광고료와 매출 간의 관계가 선형성이 크다고 할 수 있을까?
이걸 스스로 한 번 생각해보자

SE를 이용해서 가설 검증을 수행할 수 있다
null hypothesis란 것은 x와 y의 관계가
기본적으로 없다고 가정하는 것을 말하고
그 반대로 x와 y의 관계가 있다고 가정하는 것을
alternativev hypothesis라고 부른다
이걸 linear model에서의 가정들을 사용해서 수학적으로 쓰면

이렇게 표현할 수 있다
linear model을 사용하는데 x와 y의 관계가 없다고 가정하는 것은
기울기 즉, B1이 0이라고 가정하는 것과 같다
따라서 B1=0이라는 것이다
여기서 중요한 것은 B^이 아니고 true B가 0이라는 것이다
intercept는 어디에 있던지 크게 상관없다
이게 바로 null hypothesis이다
그럼 반대로 alternative hypothesis는 둘의 관계가 존재한다는거니까
기울기 즉, B1이 0이 아니라는 것이 된다

따라서 우리의 linear model이 null hypothesis인지 아닌지
알아보기 위해서는 t-statistic 식을 계산해야한다
B1^에 대조가 되는 값을 빼줘야하는데
여기서는 대조가 되는 값이 0이기 때문에 B1^-0을 해준다음
아까 말했던 standard error 값을 나눠준다
t-distribution은 정규분포와 굉장히 비슷하게 생긴 distribution인데
정규분포의 sample version인 듯 하다
linear regression model을 갖고있으면
저 t의 값은 그냥 대입만하면 바로 구해진다
그렇다면 t값을 바탕으로 위 식을 해석해보자
t의 값이 크면 B1의 값이 커지고 상대적으로 SE(B1)의 값이 작아지는 것이기 때문에
Null hypotheis가 true일 가능성이 작아지는 것이다
즉, uncertainty에 비해서 B1^이 크면 t는 계속 커지게 된다
t라는 value의 절댓값보다 큰 값을 볼 확률을 p-value라고 한다
즉, p-value가 작을수록 B1=0이라면 이런 결과가 나올 확률이 작다는 뜻이고
한 마디로 null hypothesis가 될 가능성이 작다는 뜻이다
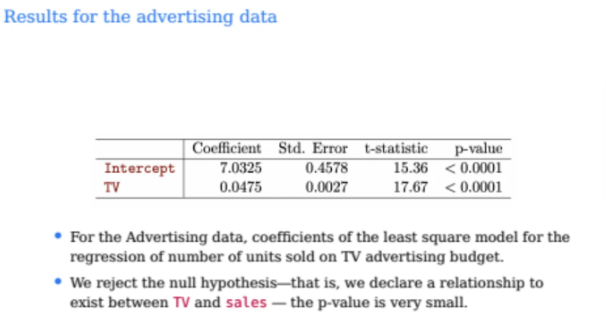
이제 그럼 지금까지 배운 내용을 바탕으로
앞의 예시에서 계산한 값들을 살펴보자
TV의 coefficient가 B1^ 값이 된다
그럼 위 결과를 보고 TV와 sales의 선형관계가
작은지 큰지 판단해보자
기울기가 0.0475가 나왔는데 이게 기울기 값이 작다고 선형관계가 약한 것일까?
절대 그렇지 않다
왜냐면 다르게 한 번 생각해보자
지금 우리가 돈 단위가 1000달러라서 기울기가 0.0475가 나온건데
만약 돈 단위를 1달러 단위로 한다면?
기울기가 엄청나게 커질 것이다
따라서 기울기의 절댓값의 크기만 가지고 선형성을 판단할 수 없다
이 linear model이 선형관계가 강한 것인지 판단하려면
coefficient와 std error의 ratio를 봐야하는데
그 값이 바로 t-statistic이다
즉, TV와 sales의 coeffificent와 std error의 비율은 17.67이 되고
만약 null이 true
즉, TV와 sales의 관계는 아예 없는데
t-statistics의 값이 17.67이 나올 확률은
0.0001 미만이라는 뜻이다
따라서 TV와 sales의 관계가 0일 확률은 매우 낮은 수준이고
이 linear model은 선형성이 꽤 강한 편에 속하게 된다
아무튼 선형성이 강한지 약한지는 이렇게
t-statistic과 p-value를 이용해서 판단해야한다

RSE는 우리가 이전에 구했던 잔차 제곱의 합(RSS)에서
n-2를 나눠준 값이다

일반 선형모델에서는 자유도가 n-2이기 때문에 n-2를 나눠준다고 한다
아무튼 이 식이 의미하는 것이 그럼 무엇이냐?
RSE는 즉 우리 모델의 잔차의 평균적인 크기를 나타낸다
한마디로 우리가 오차의 variance는 모르기 때문에
그걸 추정해주는 것이 바로 RSE가 된다
그러나 사실 RSE보다 더 많이 사용되는 것은 TSS이다
TSS는 total sum of squares인데

y값 자체의 분산값이다
TSS를 분모로 두고 TSS에서 RSS를 빼주니까
식을 정리하면 아래와 같이 된다
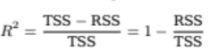
그렇다면 우리가 model을 fit을 잘 시켰다고 말하는 것은
RSS가 낮은 것을 말한다
즉, R제곱 값은 클 수록 좋은 모델이라는 뜻이 된다
TSS의 값은 그냥 y값의 분산이므로
우리가 모델링을 얼마나 잘했는지와는 크게 상관이 없다
RSS가 0이면 R제곱의 값은 1이 나오는데
적어도 이건 training data에 대해서는 잘 학습을 시킨 것이다
그렇다면 RSS가 TSS보다 큰 상황은?
이 상황은 사실 말도 안되는 상황이다
TSS의 에러가 어떤 의미인지를 잘 생각해봐야하는데
TSS는 각각의 y에서 ybar의 값을 빼준 값이다
즉, y값의 평균을 예측하면 딱 TSS가 나오게 된다
그렇다면 한마디로 RSS가 TSS보다 큰 상황은
우리가 만든 모델로 ybar(평균)조차도 제대로 맞추지 못했다는 것이 된다
정리하자면
R제곱 = 1 -> trainging data에 대해서는 완벽하게 fit
R제곱 = 0 -> 모델이 그냥 평균 ybar를 예측한 수준
R제곱 < 0 -> 모델이 평균 ybar 예측도 못한 수준
이 된다

그렇다면 또 위의 예시로 계산한 값들을 한 번 살펴보자
RSE는 오차이기 때문에 작으면 작을수록 좋은 것이다
R제곱은 지금 0.6이라는 값이 나왔는데 꽤나 큰 편이라고 한다
f-statistics도 작으면 작을수록 좋은데 다음시간에 더 자세하게 나온다고 한다

우리가 지금까지 배운건 변수가 1개인 simple linear regression이었다
그럼 이제 본격적으로 변수가 여러개인 multiple linear regression을 살펴보자
p개의 predictor가 있는 multiple linear regression은
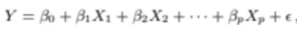
위와 같이 나타낼 수 있다
각각의 predictor에 coefficient들, 즉 파라미터들이 달려있고
상수항 포함해서 총 p+1개의 파라미터들이 있다
그렇다면 위 식에서 B1은 X1이 1만큼 증가할 때 Y1이 얼만큼
증가하는지에 대한 값이다
나머지 값들도 마찬가지이다

우리가 multiple linear regression model에서
regression coefficient를 구할 때 중요한게 있다
여러개의 predictor인 각각의 X들끼리
서로의 correlation이 0이 되는 것이 사실 가장 이상적인 케이스이다
x와 y값의 이야기가 아니라 X값들끼리의 이야기이다
아까 위에서 B1은 X1이 1만큼 증가했을 때 Y1이
얼마나 증가하는지에 대한 값이라고 했는데
이렇게 되려면 사실 각각의 X들이 서로 correlation이 없다고 가정이 되어있어야한다
그렇지 않으면 X1의 값이 변동이 있었을 때 X2도 변동할 수도 있는 것이ㅆ다
따라서 우리가 가장 먼저 해야할 것은
각각의 X들끼리 서로 correlation이 얼마인지를 체크해야하는 것이다
왜냐하면 이 correlation이 많은 경우는 estimate 자체도 사실 힘들어진다
variance들이 높아지고 해석도 당연히 힘들어진다
coefficient의 variance가 커진다는 말은 model이 unstable 해진다는 것이다
또한 한 가지 우리가 생각해야하는 점은
claims of causality를 조심해야하는 것이다
이게 무슨 말이냐하면
우리가 어떤 값들에 대해서 linear regression을 했는데
이게 positive한 기울기가 나왔다
하지만 그렇다고해서 반드시 이 값들 사이에 인과관계가 존재한다는 의미가 아니다
전혀 correlation이 없는 값들도 positive한 기울기가 나올 수 있다

아무튼 이런 multiple linear regression에서는
p+1개의 베타가 잆다
그래서 내가 estimate를 가지고 있으면
i번째 데이터포인트에 대해서는 아래와 같이 나타낼 수 있다

여기서도 RSS를 최소화하는 베타값을 찾는 것이 목표이고
아까 single linear regression과 똑같이
RSS를 구한 다음 각각의 베타에 대해서 다 미분해서 0인 점을 찾으면 된다
아까와 동일하지만 미분해야하는 베타값이 많아져서 계산이 귀찮아지는데
이를 행렬을 이용해서 굉장히 쉽게 풀 수 있다

위는 multiple linear regression인데 predictor가 2개가 있는 것이다
그래서 3차원으로 나타낼 수 있다
그럼 여기서 linear regression은 더이상 line이 아니고
hyperplane을 찾는 문제가 된다
그리고 plane에서 떨어져있는 실선들이 residual이 된다
이 residual들의 제곱의 합들을 최소화하는 파라미터를 찾아보자

이게 아까 말했던 파라미터들의 값을
행렬로 빠르게 구하는 방법이다
n개의 datapoint들에 대해서 각각의 X, Y, B 등의 값들을
이렇게 벡터로 만들 수가 있다
X의 디멘션은 n * (p+1)이 된다
그럼 우리가 잔차 제곱의 합은 선형대수에서 배운 방식대로
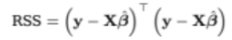
위와 같이 나타낼 수 있다
이걸 전개해서 정리하면
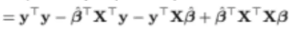
이렇게 된다
그럼 우리는 RSS를 minimize하는 베타값을 찾는 것이 목표라서
위식을 B^에 대해서 미분해서 0이 되는 값을 찾으면 된다
행렬의 미분 규칙은

이렇게 정리할 수 있고 따라서

이렇게 나타낼 수 있다
따라서 위 식을 0을 만드는 B^을 구하면
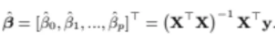
이렇게 나오는데
이건 그냥 무조건 외워야하는 식이라고한다
따라서 누군가가 multiple linear regression에서
RSS를 최소로 만드는 B^ 행렬을 구하라고 한다면

위 식이 바로 나올 수 있도록 외워놓자
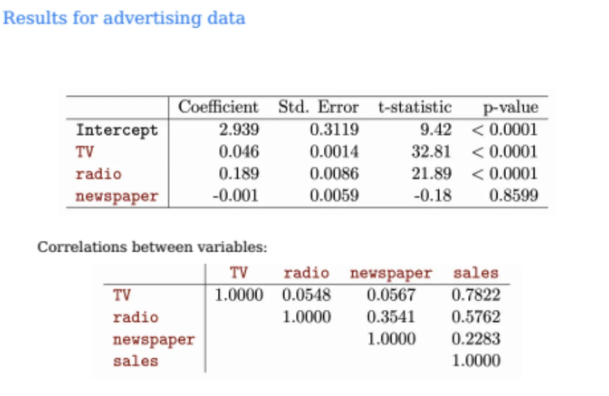
그렇게 해서 처음의 예시
TV, radio, newspaper 3개의 feature에 대해서 계산을 수행하였다
각각의 B1^, B2^, B3^ 값들과
해당 값의 std error, t-statistic, p-value를 정리하였다
t-statistic의 값이 TV가 radio보다 더 크기 때문에
선형관계는 TV가 radio보다 더 강한 것이 된다
p-value가 0.05 이하가 되면 보통 충분히 significant하다고 말하는데
따라서 TV와 radio는 significant하다고 말할 수 있다
TV와 radio 각각 sales와 상관관계가 없다고 가정했을 때
t-statistic의 값이 이렇게 extreme한 것을 볼 확률이 0.0001 미만이라는 뜻이다
그렇다면 newspaper는?
t-statistic의 절댓값도 낮고(ratio도 낮고)
p-value가 0.85이기 때문에 null이 true일 때
꽤 빈번하게 이런 경우를 볼 수 있다는 말이 된다
따라서 variables간의 correlation을 계산해보면
TV와 sales가 가장 강한 양의 상관관계를 보이며
radio와 sales는 중간 정도의 양의 상관관계를
newspaper와 sales는 상관관계가 크게 없다고 해석할 수 있다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [ML] Resampling Methods 1편 (Cross-Validation) (0) | 2025.09.21 |
|---|---|
| [ML] Classification 2편 (LDA, QDA, Naive Bayes) (1) | 2025.09.16 |
| [ML] Classification 1편 (Logistic Regression) (1) | 2025.09.15 |
| [ML] Linear Regression 2편 (F-statistics, categorical predictors, interactions) (0) | 2025.09.09 |
| [ML] Overview of Machine Learning (3) | 2025.09.02 |