본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다
지난시간까지 Linear Regression에 대해서 배웠다
이번에는 Logistic Regression에 대해서 배워본다

Logistic Regression은 우리가 흔히 말하는
Classification를 해결하는 방법이다

Classification 문제란 우리가 모델을 통해서 예측해야하는 output
즉, response variable이 category인 것을 말한다
위 ppt에서 예시를 살펴보면
눈의 색상이 brown, blue, green 3개 중에 1개를 맞춰야한다거나
email을 보고 스팸인지 스팸이 아닌지 맞춰야하는 경우가 있다
즉, classification이라는 것은 X라는 feature를 가지고
어떤 classifier인 C에 넣은 다음
그 output의 category space로 mapping을 해주는 문제이다
바로 그렇게 해주는 classifier 함수 C(X)를 찾는 문제이다
그리고 보통 카테고리들 중에서 어떤 카테고리로 갈지 바로 매핑하는 것보다
카테고리별로 확률을 계산하는 것이 더 유용하기 때문에 그런방식으로 한다
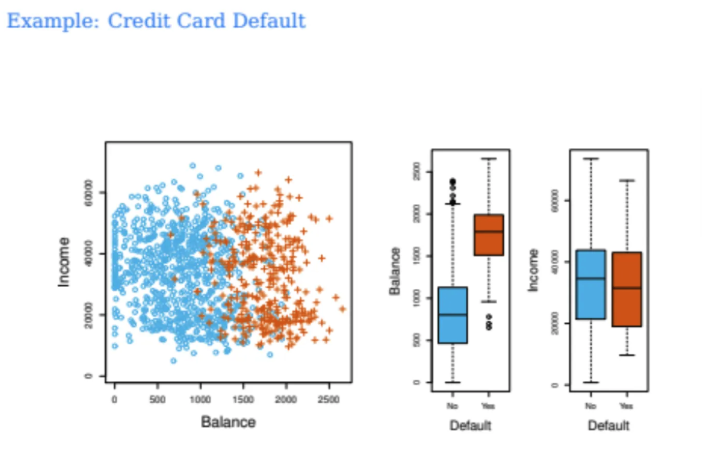
이번에는 Credit Card Default 예시를 한 번 살펴보자
왼쪽에서는 Balance와 Income 모두 X feature variable이다
각각의 포인트들은 사람들이고
연체가 되었으면 십자고 모양, 연체가 되지 않았으면 동그라미이다
오른쪽 boxplot에는 연체여부가 yes or no로 되어있고
variable들의 분포를 box로 표현하고있다
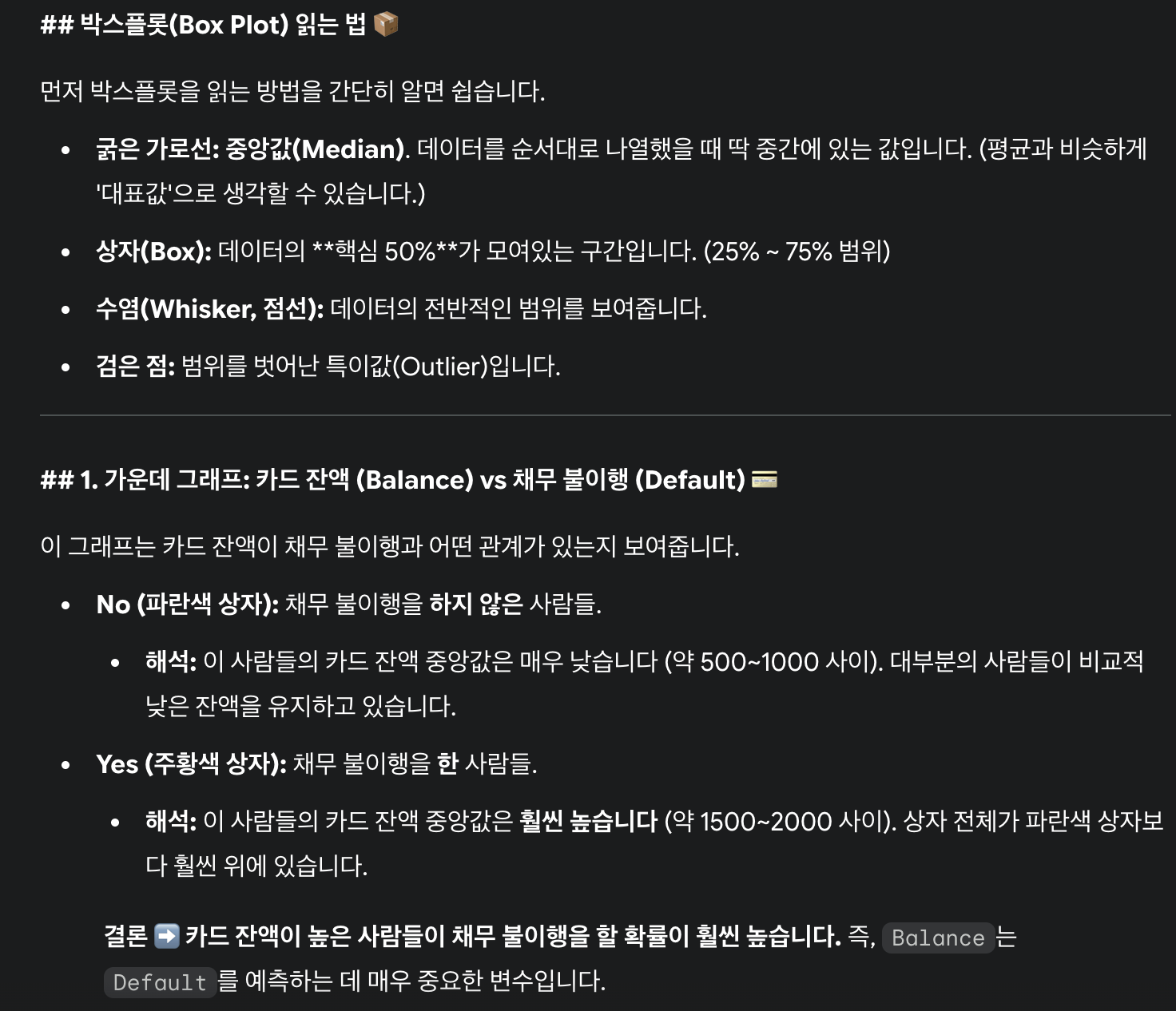
대충 육안으로 데이터를 살펴보자
지난달 카드 사용량이 많은 사람들이 연체율이 더 높아보이는 것 같다
그리고 income이랑은 크게 상관이 없는 것 같아 보인다
물론 이런 데이터를 육안으로 보고 판단할 수 있는 것도
2-dimension이니까 가능한 것이다

그런데 천천히 생각해보면
이전에 linear regression을 배울 때
categorical한 feature에 대해서 0 또는 1을 넣어서
수행해준 것이 기억이 날 것 이다
그럼 그냥 그렇게 해주면 되는거 아닌가?
위 경우 연체가 된 경우 1, 그렇지 않은 경우 0을 넣으면 될 것이다
어차피 우리가 구하고 싶은 response variable을
연체자일 확률이라고 정의하면 되는 것 아닌가?
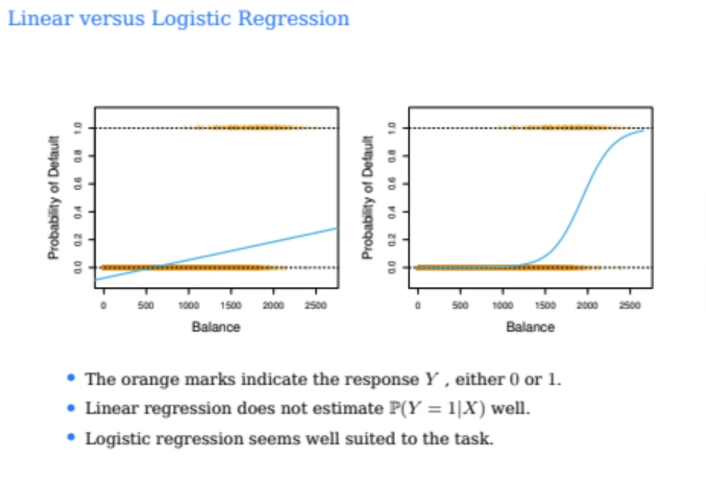
그럼 실제로 그렇게 수행한 결과를 한 번 살펴보자
왼쪽이 위 예시를 실제로 linear regression으로 수행한 것이고
오른쪽이 오늘 우리가 배울 logistic regression으로 수행한 것이다
우선 왼쪽 Linear regression을 잘 살펴보자
우리가 알고자하는 것은 확률값인데 balance가 500이하일 때 음수가 나온다
또한, 우리가 위에서 실데이터를 보았을 때
balance가 2000 이상이면 대부분 거의 다 연체가 되었었다
하지만 왼쪽 Linear regression에서는
balance가 2000이상이어도 확률이 0.3정도밖에 안되는 것을 확인할 수 있다
즉, linear regression으로 했을 때
데이터에 잘 fit되지 않았다는 것을 알 수 있다
또한, 가장 큰 문제점은 우리가 구하고자하는 것은 확률값인데
예측값이 0과 1사이에 존재하지 않을 수도 있다는 것이다
따라서 이러한 classification 문제는 그냥 linear regression으로 하기보다는
다른 새로운 분류를 위한 model이 필요하다
그게 우리가 오늘 배울 logistic regression이고
logistic regression은 늘 예측값이 0과 1사이에 위치해있고
오른쪽 그림처럼 완만하게 가다가 갑자기 확 1에 가까워지는 형태이다

앞의 예시는 response variable의 class가 0과 1 2개였지만
만약 2개가 아니고 여러개라면?
위 예시에서는 response variable이
1, 2, 3 3개인 예시이다
하지만 위처럼 이렇게 linear regression으로 풀기 위해서
stroke이 1, drug overdose가 2, epileptic seizure이 3이라고 한다면
사실상 각 class별 차이가 같다고 가정하는 것이다
이게 무슨 말이냐하면
stoke(1)과 drug overdose(2)의 차이가 1이고
drug overdose(2)와 epileptic seizure(3)의 차이가 1이니까
각 질병 간의 차이가 동일하다고 가정하는 것이다
하지만 현실적으로는 이렇게 각 class간의 차이가
서로 동일하다고 가정할 수 없다
따라서 이렇게 response variable이 여러 개인 분류를 수행할때도
multiclass linear regression이 아닌
multiclass logistic regression을 사용해야한다

logistic regression은 결국 어떤 conditional class의
확률을 구하는 문제이다
우리는 P(X)를 P=(Y=1|X)로
즉, X feature를 넣었을 때 Y=1(연체 O)일 확률을 구해보자
logistic regression은 수식을 아래와 같이 모델링한다

오일러상수 e는 고정값이니까
e의 지수가 커지면 커질수록
P(X)의 값은 1에 가까워진다
그리고 e의 지수가 작아지면 작아질수록
P(X)의 값은 0에 가까워진다
결국 P(X)의 값은 반드시 0과 1사이의 값으로 나온다는 것이다
그리고 B0과 B1이 우리가 학습시켜야할 파라미터이다
위 식을 조금만 변형하면
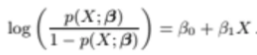
위와같이 정리할 수 있는데
분자는 그냥 P(X)이고 분모는 전체 1에서 P(X)를 뺀 값이 된다
분모값은 1-P(X)라서
X가 주어졌을 때 Y=0일 확률이 되는데
이를 odds라고 한다
따라서 위 정리된 식은
no일 확률과 yes일 확률의 ratio이다
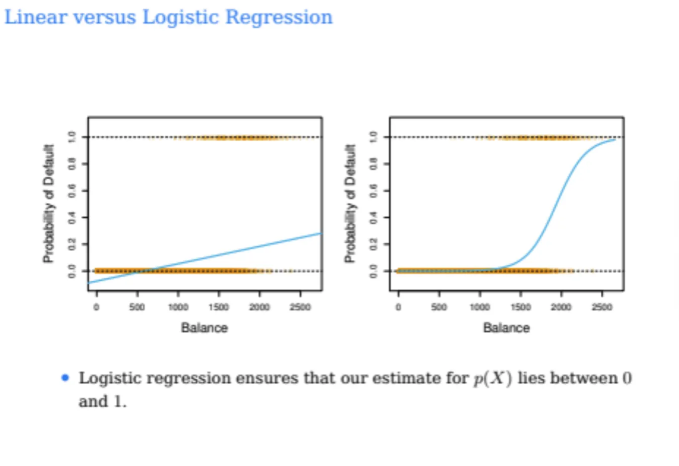
아까 앞에서 봤던 그래프이다
오른쪽이 logistic regression이다
오른쪽 logistic regression은 sigmoid 함수를 그리는 것인데
이 친구가 어느 시점에서 완만하게 가는지
어느 시점에서 steep해지는지
이런 모양들은 파라미터들이 결정해주게 된다
따라서 이 파라미터들을 학습시켜서
저 sigmoid 함수의 모양을 알고싶은 것이다

그렇다면 이걸 어떻게 학습시킬까?
우리가 이전에 배운 linear regression은
어떻게 파라미터들을 학습시켰는지 다시 생각해보자
그땐 least sqaure를 계산해서 학습시켰었다
저렇게 하면 2차함수가 나오고 2차함수는
convex 함수이기 때문에 최적화를 하기 좋은 case였다
그럼 마찬가지로 우리는 위 상황에서도
어떤것을 어떻게 최적화시켜야하는지 생각해보자
그렇다면 여기서 좋은 모델이 되려면
y=1인 데이터에 대해서는 P(X)는 1에 가깝게 나와야하고
y=0인 데이터에 대해서는 P(X)는 0에 가깝게 나와야한다
우선 우리는 모든 데이터포인트들이 서로 독립한다고 가정하므로
각 데이터포인트들을 넣었을 때 나오는 확률값을
모두 곱해주자
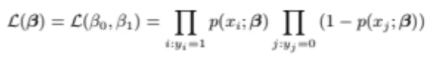
이를 likelihood라고 한다
그렇다면 위 likelihood 값을 잘 사렾보자
앞의 항은 y가 1인 데이터 포인트들을 넣었을 때의
P(X)값이기 때문에 이는 1에 가까울수록 좋은 것이다
그럼 뒤의 항은 y가 0인 데이터 포인터들을 넣었을 때
1-P(X)의 값이므로 결국 y가 0인 데이터포인트들을 넣었을 때
이를 0이라고 뱉을 확률값과 동일하므로
이 항의 결과도 결국 1에 가까울수록 좋다
따라서 우리의 목표는 이 likelihood 함수를 가장 크게 만드는 것이 되고
이를 maximum likelihood estimation이라고 한다
그러나 이러한 곱셈을 maximize하는건 상당히 어려운 문제인데
이걸 충분히 풀 수 있는 문제로 바꿀수가 있다

곱셈은 maximize하기에 힘들기 때문에 우리는 이를 어떻게 변형시키냐?
바로 log를 씌워준다
log를 씌우면 곱하기는 덧셈이 되고
log 함수는 monotone increase 함수이기 때문에
로그함수의 maximum값 자체와 likelihood의 맥시멈값 자체가 동일하지는 않지만
두 함수 모두 maximum값이 되는 베타
즉, argument의 값은 동일하다
또한 log likelihood 함수 자체가 완만해진다

likelihood 함수에 Log를 씌우면 확실히 최대화시키는게 쉬워진다
그렇다면 우리는
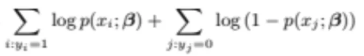
위 식을 최대화시키고 싶은 것이다
그럼 우리가 이전에 했던 linear regression처럼
그냥 미분을해서 미분값이 0인 것을 찾으면될까?
무작정 그렇게 하면 안되고
우선 저 함수가 어떤 모양인지를 알아야한다
우리가 이전에 봤던 linear regression의 RSE는
convex 함수였는데 위 log-likelihood 함수는
concave 함수이다
concave 함수는 미분했을 때 0인점이
maximum인 점이기 때문에
똑같이 미분해서 0인 점을 찾아내면된다
위 식을 베타0, 베타1에 대해서 미분하면

위와같이 결과가 나오게 된다
그럼 미지수가 2개, 식도 2개이므로
우리는 찾고자하는 파라미터값들을 찾아낼 수가 있다
linear regression은 이런 파라미터들을
closed form으로 정의할 수 있었다
하지만 logistic regression은 linear regression과 다르게
만족하는 베타식들을 딱 쓸 수가 없다
iterative하게 계산해가면서
어느 점에 수렴했을 때 maximum이 되는지 찾을 수 있는데
이 과정을 수식으로 한 번에 정리할 수 없기 때문이다
이렇게 iterative하게 미분이 0인 점을 찾아가는게
gradient descent의 개념이고
나중에 deep learning을 할 때 요긴하게 사용된다

아무튼 위의 과정을 활용해서
log-likelihood를 maximize 시켜서
estimate를 해보자
실제로 구한 결과를 보면 B0은 -10.6513이고
B1이 0.0055이다
linear regression을 생각해서 B1이 기울기값이라고 생각하면 안된다
이건 balance가 1만큼 증가할 때
log odds가 B1만큼 증가한다고 해석해야한다
즉, 신용카드 잔액(balance)가 1단위만큼 증가할 때
연체(default)될 log odds가 0.0055만큼 증가한다는 의미이다
이제 이 estimate를 보고 B^값이 significant한지 살펴보자
이건 z-statistic와 p-value를 확인해보면 알 수 있다
p-value가 0.0001인 것을 봐서 B0^과 B1^모두
significant한 것을 알 수 있다
따라서 null hypothesis는 reject 될 것이고
두 데이터가 충분히 연관된 데이터임을 알 수 있다
그렇다면 만약 null hypothesis가 true가 되어서
balance가 default에 영향을 미치지않는다면 어떻게 될까?
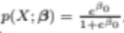
그렇다면 P(X)의 값은 이렇게 될 것이다
balance 값과는 상관없이 항상 동일한 결과가 나오는 것이다

그렇다면 어떤 사람의 지난달 카드값이 1000달러였다고 해보자
그 사람이 default 할 확률은?
X에 1000을 넣으면 되니까
직접 이렇게 게산을 해보면 0.006
즉, 0.6%로 아주 작은 값이 나온다고 한다
그런데 만약 그 사람 카드빚이 2000달러로 늘었다고해보자
그래서 똑같이 계산하면 0.586
즉, 0.58%가 나온다고 한다
그럼 확률이 거의 50배 이상 늘어나게 된 것이다
우리가 아까 그래프에서 살짝 봤듯이 logistic regression
즉, sigmoid 함수는 확 늘어나는지점이 있고
그 지점이 어디인지는 파라미터가 정해준다

그렇다면 이번에는 student라는 새로은 predictor를 이용해서
다시 estimate를 해보자
학생일 때를 1로 넣고 그렇지 않을 때를 0으로 넣어서
파라미터 값들을 계산했더니 위와 같은 결곽 나왔다
그럼 p-value를 보니까
student인 것이 default 여부와 관련이 있나?
B1^이 0.4049
즉, 양수값인 것을 보니 학생이면
default될 log odds가 증가하는 것을 알 수 있다
실제 확률만 봐도 학생일 때는 연체할 확률이 0.0431이고
학생이 아닐 때는 연체할 확률이 0.0292가 나오는 것을 알 수 있다
따라서 실제로 학생이냐 아니냐가
default 여부에 영향을 미친다고 추측할 수 있다
그렇다면 이제 balance, income, student와 같은
여러 개의 feature를 한꺼번에 담아보자

feature에 balance, income, student 3개를 넣었다
우리가 이전에 해준 것과 동일하게
오일러상수 e의 지수값에 그냥
multiple linear regression을 넣듯이
추가되는 파라미터들을 여러 개 넣어주면 된다
파라미터 개수가 늘어난 것 뿐이지 사실상 똑같다
똑같이 log-likelihood를 maximize하는 미분해서 0인 값을 찾아내보자
그렇게 계산해서 나온 결과가 위와 같다
위 결과를 봤을 때 balance는 default와 연관이 있음을 확인할 수 있다
그렇다면 income은?
p-value가 0.7115인 것으로 봐서 significant하지 않다
따라서 income은 default에 큰 상관이 없는 것이다
자 그러면 이제 마지막으로 student를 한 번 살펴보자
우리가 아까 앞에서 student만 feature로 넣고
logisitic regression을 수행했을 때는
파라미터값이 양수여서
student일수록 default할 확률이 높다고 추측했다
하지만 위 결과에서는 파라미터가 음수가 나오는 것을 확인할 수 있다
이 모델에서는 앞에서의 모델과 달리
학생이면 default 될 확률이 더 낮다고 말하고 있다
그리고 얘의 p-value도 확인해보건데 significant함을 알 수 있다
그렇다면 우리는 2개의 상반된 결과 중에서
어떤 것을 믿어야할까?
위 문제는 cofounding이라고 하는 문제인데
단지 logistic regression에서만 발생하는 문제는 아니다
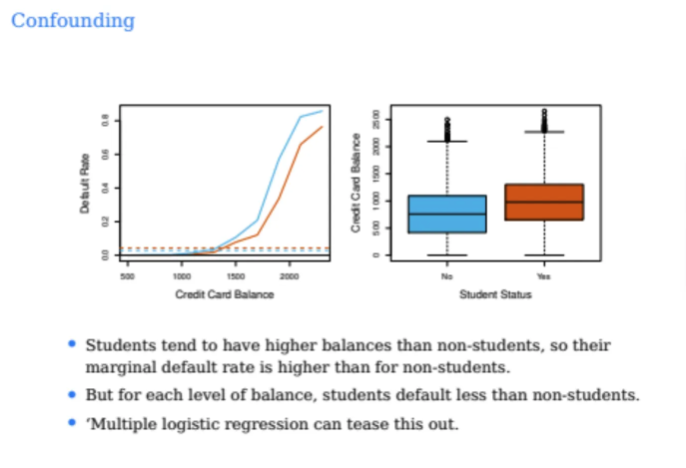
위 그래프를 한 번 잘 살펴보자
파란색이 학생이 아닌 사람들의 balance와 default rate이고
주황색이 학생인 사람들의 balance와 default rate이다
왼쪽 그래프를 살펴보면
학생이나 학생이 아닌 사람이나 마찬가지로
balance가 높을 수록 연체율이 높아지는 것을 확인할 수 있다
그러나 동등한 balance에서 비교해보았을 때
연체율은 학생보다 비학생인 사람이 더 높다
그런데 오른쪽 boxplot에서 확인해보니
학생들이 그냥 전반적으로 비학생들에 비해서
balance가 많음을 확인할 수 있다
따라서 우리가 다른 feature들 없이 학생 feature만 보면
학생집단이 balance가 높기 때문에 default 확률이 더 클 수 있다
하지만 동일한 balance 수준에서 보면
학생이 비학생보다 default를 덜 하는 것을 알 수 있다
즉, 두번째에서 본 여러 feature들을 넣었을 때 나온 결과가 더 합리적이라는 것이다
즉, balance라는 중요한 변수를 고려하지 않으면
위와 같이 잘못된 결론에 다다를 수 있게 된다
따라서 우리가 데이터를 갖고 있는데
y값에 영향을 미칠 것 같은 feature들을 넣지 않아서는 안된다
그런 feature들을 다 포함시키지 않는다면
실제 true 관계를 얻지 못할 수가 있게 된다

gpt한테 설명에 대해서 정리를 해달라고 했는데
그 죄(?)를 뒤집어썼다고 말하는 표현이 웃겨서 올려본다..

우리가 지금까지는 class가 딱 2개인 것만 다뤘다
그런데 2개보다 더 많은 class를 가질 때 어떻게 할 수 있을까?
조금 더 복잡해지긴하지만
X가 주어졌고 파라미터가 베타 기준으로 그냥 y값이 0, 1인 것이 아니고
class가 k인거고 총 K개의 class는 1부터 k까지 존재하게 된다
그리고 다음과 같이 class에 해당하는 파라미터들이 존재하게 된다
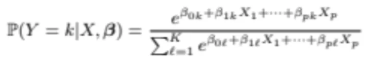
위 예시는 multiple regression으로 하는 것이니까 feature도 p개가 된다
그렇다면 class k에 대한 파라미터 set이 1개가 있고
class k+1에 대한 파라미터 set이 또 1개가 있고
class k+2에 대한 파라미터 set이 또 1개가 있고...
이런식으로 class마다 파라미터 set이 존재하게 된다
그렇다면 총 파라미터는 몇 개가 될까?
한 class당 파라미터가 p+1개가 되니까
(p+1)*K가 된다
그렇다면 이걸 어떻게 학습시키나?
우리가 지금까지 배웠던 log-likelihood로 충분히 구할 수 있다
simple logistic regression부터 시작해서
한 번 직접 계산해보는 것을 추천한다고한다
만약에 우리가 이 logistic regression의 계산 과정을 모른다면
그냥 프로그래밍 할 때 built-in 함수만 사용하는 것인데
이는 공부를 하는 아무런 의미가 없다
원래는 K개의 class가 있으면
K개의 파라미터 set가 모두 있어야하지만
확률이기때문에 전체 합이 1이 되어서
사실상 K-1개만 되어도 된다
따라서 한 개의 class를 기준점으로 잡으면
나머지 확률을 상대적으로 비교해서
나머지 K-1개만 학습시키면 된다


'강의 > machine learning & deep learning' 카테고리의 다른 글
| [ML] Resampling Methods 1편 (Cross-Validation) (0) | 2025.09.21 |
|---|---|
| [ML] Classification 2편 (LDA, QDA, Naive Bayes) (1) | 2025.09.16 |
| [ML] Linear Regression 2편 (F-statistics, categorical predictors, interactions) (0) | 2025.09.09 |
| [ML] Linear Regression 1편 (single & multiple linear regression) (0) | 2025.09.08 |
| [ML] Overview of Machine Learning (3) | 2025.09.02 |