본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간에는 bootstrap에 관한 내용을 살펴본다

bootstrap은 우리 지난 시간에 배웠던
cross validation과 비슷한 맥락이다
이 bootstrap은 하나의 dataset을 이용해서
여러 복제본 dataset을 만드는 방법인데
아주 유용해서 자주 쓰이는 방법이라고 한다
예를 들어서 데이터셋 하나로 어떤 모델의 파라미터를 구했다고하자
이 데이터셋 한개만으로는 파라미터의 uncertainty를 계산하기가 힘들다
우리가 앞에서 linear regression과 logistic regression은 가능했지만
원래는 쉽지 않다고 한다
따라서 bootstrap이 이런 상황을 해결해줄 수 있다고 한다

그렇다면 bootstrap은 뭘까?
개발자들이 말하는 bootstrap과는 완전히 다른 개념이라고 한다
bootstrap은 위에서 잠깐 설명했지만
아주 쉽게 설명하면
갖고 있는 데이터를 쥐어짜서 더 얻을 수 있는 정보를 얻는 방법이다

위처럼 파라미터 알파를 모델링도 아니고
아주 simple하게 통계량을 계산했다
2개의 financial asset이 있고 X와 Y가 있다
각각 다른 종목이고 서로 다른 random variable이다
우리가 X, Y 종목에서 X에는 알파만큼을
Y에는 1-알파만큼을 투자한다고 생각해보자
우리가 하고자하는건 risk를 최소화시키는 것이다
위 상황에서 우리가 투자를 통해 얻을 수 있는 자산은
X*알파 + Y * (1-알파)이다
그리고 risk는 위 식에서 variance이다
따라서 risk를 최소화한다는 것은
variance를 최소화해야한다는 것이다
minimize 시켜아하는 variance는 closed form으로 나타낼 수 있다
아주 simple하게 random variable인 X, Y의
balance를 맞춰서 variance를 minimize시키는 것이다

이 minimize 시켜야하는 식을 결국 시그마로 계산해야한다
그런데 우리는 X의 true variance를 알 수가 없고
Y의 true varaince도, true covariance도 알 수가 없다
우리가 갖고 있는 것은 X라는 Random variable의 실제 정확한 분포가 아닌
그 분포에서 오는 sample들만 갖고 있다
물론 Y도 마찬가지이다
그냥 우리가 sample들만 가지고 estimate를 하는 것이다
그래서 나온게 variable hat의 값이다

여기서 각각 보이는게 X, Y를 나타내는 하나의 dataset이다
이렇게 dataset이 있으면 X와 Y의 variance, covariance들도 다 구할 수 있다
따라서 첫번째 데이터셋에서 알파값을 구하면
0.576이 되고
각각 데이터셋들마다 0.532, 0.657, 0.651
이렇게 알파햇의 값이 구해진다고 한다

이렇게하면 알파햇에 대한 분포를 알 수 있다
그래서 우리는 4개의 큰 데이터셋들로 값을 구했기 때문에
알파햇 값의 표준편차를 구할 수 있다
실제로 1000개의 dataset으로 나눠서 1000개의 알파햇에 대한 분포를 그린 것이
왼쪽 주황색 그래프이다
그리고 핑크색 선은 분포를 안다고 가정했을 때 가장 이상적인 알파값이다
오른쪽 파란색 그래프는 bootstrap으로 데이터들의 copy를 만들어서
알파의 분포를 나타낸 것이다
주황색 그래프에서 true optimal 값을 보면 0.6인데
오른쪽 파란색에서 bootstrap으로 데이터를 복사해서 만들어낸
optimal 값이 0.5996이 나왔다
따라서 두개의 값이 꽤나 유사함을 알 수 있다

단순히 알파햇만 구하는게 아니고
알파햇의 standard deviation까지 구할 수 있으면
해석하기도 쉬워지고 우리가 구한 값이 얼마나 stable한지도 알 수 있다

그렇다면 이제 실제 현실을 한 번 살펴보자
우리가 real world에서 데이터셋을 100개 1000개를 막 가져올수가 없다
그래서 bootstrap을 활용해서 한 개의 데이터셋만을 가지고
새로운 데이터셋들을 얻는 결과를 가져오고 싶은 것이다
따라서 bootstrap은 원래 데이터셋에서 얘를 복사를 한다
랜덤으로 뽑아서 copy하는데 이때 중요한건
with replacement로 뽑는다는 것이다
즉, 복원추출을 한다는 뜻이다
예를 들어서 내가 환자 데이터를 대상으로 실험을 한다고 하자
그런데 데이터가 부족하다고해서 마음대로 환자수를 늘려서 데이터를 만들고 할 수가 없다
따라서 지금 갖고있는 데이터만으로만 실험을 해야한다
따라서 갖고 있는 데이터를 복사를 하려고 한다
그런데 진짜 동일한 데이터를 그냥 복사를 하면 아무런 의미가 없다
그래서 우선 우리가 실제로 가진 데이터가 들어있는 original box와
우리가 복사한 데이터들이 들어갈 copy box가 있다고 하자
그래서 우리는 original box에서 원본 데이터들을 뽑아서
복사해서 copy box에 넣는다
그런데 이 때 한 번 뽑힌 데이터라고해서 original box에서 제거하는것이 아니라
나중에 또 뽑힐 수 있게 그대로 둬야한다
이게 바로 sampling with replacement(복원추출)이다
따라서 위 과정을 우리가 원하는 개수만큼 해주면 되는게
이게 바로 bootstrap이다
이렇게 복원추출로 복사해서 생성한 데이터를
bootstrap dataset이라고 부르는데
이 bootstrap dataset은 original dataset과 완벽하게 일치하지 않는다
bootstrap에는 어떤 데이터는 여러번 들어가있을 수가 있고
또 어떤 데이터는 아예 들어가지 않을 수도 있다
그런데 통계적으로 bootstrap은 original dataset과
동일한 분포를 지닌다고한다
따라서 이렇게 단순한 방법으로 같은 분포를 띄는 데이터셋을 만들 수 있기때문에
bootstrap은 굉장히 많이 사용되는 방식이라고 한다
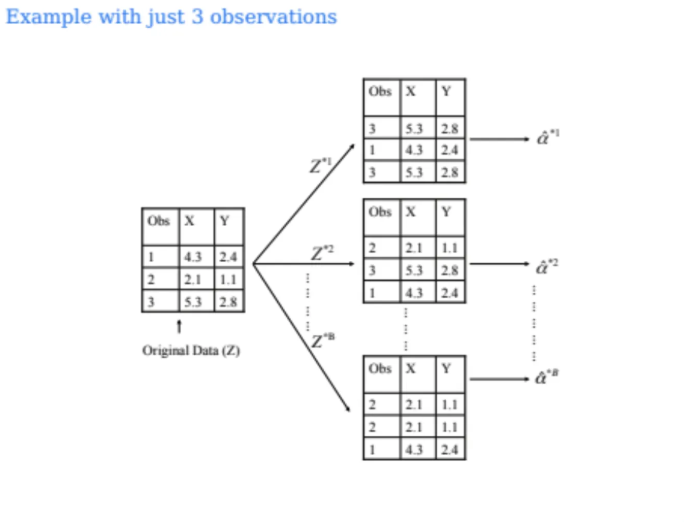
위는 bootstrap을 수행한 예시이다
original dataset이 3개가 있다고 하면
3개의 bootstrap dataset을 만든다
이렇게 각각의 bootstrap dataset을 만들면서
original dataset과 개수가 같아지면 멈춘다
따라서 이걸 우리가 원하는만큼 수행할 수 있는 것이다
이렇게 알파햇들을 각각 구해서
min값을 구할 수도 있고 분포도 구할 수 있고 그런것이다

B개의 bootstrap 데이터를 만들어서 standard error를 구할 수 있다
위 내용에 대해서 수업하면서
어떻게 복원추출을 하는데 original dataset과 데이터의 분포가 동일하냐?
라는 질문이 정말 많이 나왔는데
뭐 통계적으로 이미 증명이 된 내용이라고 한다..ㅎ

bootstrap을 수행할 때 우리가 조심해야할 점이 하나 있다
바로 bootstrap은 모든 데이터들이 서로 관련이 없어야한다
time series data로 예를 들어보자
time series data는 데이터들이
이전의 데이터에 의해 종속되는 구조이다
따라서 데이터들끼리 서로 연관이 되어있는 것이다
이런 데이터는 bootstrap을 해도 같은 분포가 되지 않는다
어떤 상황에서도 데이터가 서로 correlated되면 분포가 달라지기때문에
반드시 서로 correlated 되지 않은 데이터로 bootstrap을 수행해야한다

그렇다면 이러한 bootstrap을 가장 유용하게 쓰는 경우는 언제일까?
그건 바로 standard error를 구할 때이다
이러한 standard error를 구하면 데이터셋의 confidence를 구할 수 있다
위와같이 Random Varaiable을 bootstrap을 활용해서
confidence interval가 95%가 나온다면
dataset 100번을 sample했을 때 95개 정도가 true를 포함한다는 뜻이다

그럼 이 bootstrap을 갖고 Prediction error도 구할 수 있을까?
이건 당연히 안된다
왜 안될까?
bootstrap은 각 dataset들간에 중복되는 데이터가 존재하기 때문이다
지난시간에 배웠던 k-fold cross validation에서는
prediction error를 추정해서 구할 수가 있었는데
그렇게 할 수 있었던 이유는
각 fold간에 데이터들을 절대 overlap시키지 않았기 때문이다
실제로 bootstrap에서 각 데이터가 중복될 확률은
3분의 2정도라고 하는데
n번 반복했을 때 어떤걸 빼고 나머지가 다 들어갈 확률은
(1-1/n)n제곱이 된다
이걸 극한으로 보내면 3분의 1이 되는데
어떤 데이터가 포함되지않을 확률이 3분의 1인것이기 때문에
데이터가 포함될 확률은 3분의 2가 된다고한다
아무튼 bootstrap은 중복되는 데이터가 발생하기 때문에
prediction error를 측정할 수 없다

그런데 위 데이터 중복으로 인한 prediction error를 추정하지 못하는 문제를
해결하는 방법이 있다고 한다
우리가 bootstrap을 수행하다보면
한 번도 뽑히지 않은 데이터가 발생할 수도 있다
이걸 Out Of Bag(OOB)라고 부르는데
이 OOB 데이터들만 모아서 이걸 test dataset처럼 사용할 수 있다고 한다
물론 이렇게해서 할 수는 있지만
만약에 우리의 목적이 test error estimation이라면
이전시간에 배웠던 cross validation을 사용하는 것이 적절하다
이 OOB 개념은 나중에 tree model에서 앙상블 bagging에서 다시 나오니
기억해두면 좋을 것 같다
그렇다면 이 bootstrap은 어떤 경우 유용할까?
우리가 앞에서 linear regression과 logistic regression은
파라미터들에 대한 standard error를 구할 수 있었다
따라서 굳이 bootstrap이 필요한가?라고 생각할 수 있다
하지만 우리가 뒤에서 배울 decision tree같은 모델은
standard variance를 구할 수가 없다
따라서 이런 경우에 bootstrap을 자주 사용한다고 한다
bootstrap은 모델에 구애받지 않기 때문에
어떠한 모델이든 generic하게 사용할 수 있다
그래서 neural network에서도 많이 사용되는 방식이다
또한 가장 강력한 bootstrap의 장점 중 하나는
예측 성능 자체를 높여준다는 것이다
예를 들어서 우리가 prediction을 수행할 때
bootstrap dataset을 10개를 만들었으면
각각에 대한 모델도 10개가 나올 수 있다
그럼 각 모델에 대한 output도 모두 10개가 나올텐데
이걸 평균을 내는게 실제로 성능이 훨씬 좋아진다고 한다
왜냐하면 각각의 모델은 하나의 random sample인데
ㅇㅣ걸 평균을 내면 variance가 굉장히 줄기 때문이다
따라서 실제로 bootstrap의 이러한 강점을
앙상블모델이라는 걸로 활용하고있다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [ML/과제 1] Linear Regression, Logistic Regression scikit-learn으로 구현하고 결과 분석하기 (0) | 2025.10.08 |
|---|---|
| [ML] Subset Selection 1편 (Best Subset Selection, Stepwise Selection) (0) | 2025.09.30 |
| [ML] Resampling Methods 1편 (Cross-Validation) (0) | 2025.09.21 |
| [ML] Classification 2편 (LDA, QDA, Naive Bayes) (1) | 2025.09.16 |
| [ML] Classification 1편 (Logistic Regression) (1) | 2025.09.15 |