본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간과 다음 시간에는
tree-based methods에 대해서 배운다고한다
오늘은 가장 기본이 되는 내용인 deicision tree에 대해 배운다

decision tree라는 이름만 듣고 classification이라고 착각하는 경우가 있는데
이 decision tree는 regression과 classification 2개 다 사용할 수 있다
decision tree란 x predictor space가 있는데
이걸 어떻게 하면 partition을 나눠서
partition 안에 있는 y값들이 어떤 prediction을 갖는지를 찾는 과정이다
한 마디로 우리가 어떻게 하면
predictor space 안에서 잘 segmentation을 할까에 대한 얘기이다
이게 decision tree를 통해서 우리가 해결하고자하는 과제이고
이걸 우리는 tree라는 방식으로 해결하겠단 소리이다
그리고 여기서 decision이라는 것은
결국 어디서 어떻게 자를까에 대한 결정이란 뜻이다
따라서 regression과 classification 모두 가능하다

우리가 오늘 배울 tree-base methods는
굉장히 단순하고 직관적인 방법이다
즉, 해석이 쉽다는 뜻이다
x의 dimension이 많더라도 사실 우리가 tree로 표현할 수 있기 때문에
그냥 2D로 시각화해서 볼 수 있다는 장점이 있다
우리가 오늘 배울 decision tree만을 봤을 때는 매우 심플하지만
다음 시간에 배우는 방법들은 tree-based model이긴 하지만 조금은 복잡하다
아무튼 그래서 오늘 배울 decision tree만으로는
prediction accuracy가 그렇게 높지 않을 수는 있다
이렇게 복잡한 모델과 단순한 모델의 장단점은 명확하다
우리가 다음 시간에 배울 내용은 bagging, random forest 이런 내용인데
이건 실제로 현업에서도 매우 널리 사용되는 방법이고
실제로 성능도 매우 좋다고 한다
위 내용들은 그냥 1개의 tree가 아니라
많은 트리들을 다 combine해서 어떻게 해서
performance를 improve 할 수 있을까에 대한 내용이다
그 과정에서 우리가 저번 시간에 배운 bootstraping도 사용한다
하지만 이번 시간에는 그냥 단순 decision tree만 배워보자

위 예시는 그냥 단순 classification 문제이다
뭐 질병이 있는지 없는지.. 그런 관련 문제라고한다
age랑 start라는 2개의 x variables이 있고
absence가 초록색, present가 빨간색이라고 한다
우리가 이번 시간에 배워볼 것은
어떻게하면 이런 것들을 잘 잘라서
feature space에서 가장 왼쪽의 tree 구조로 만들어서
prediction에 용이하게 만들지이다
예를 들어서 start가 8.5 이상이면 위 예시에서는 오른쪽으로
그렇지않으면 왼쪽으로 가도록 rule을 정한다
이런 식으로 계속 partition을 나누다보니
결과로 왼쪽 3개는 absence가 오른쪽 2개는 present가 나오게 되는 것이다
이게 지금 변수가 2개라서 시각화가 가능하다고 생각할 수 있는데
실제로는 feature가 2개보다 더 많아도
왼쪽 그림처럼 그냥 tree로 시각화가 가능하다
그래서 해석이 매우 용이해지는 것이다
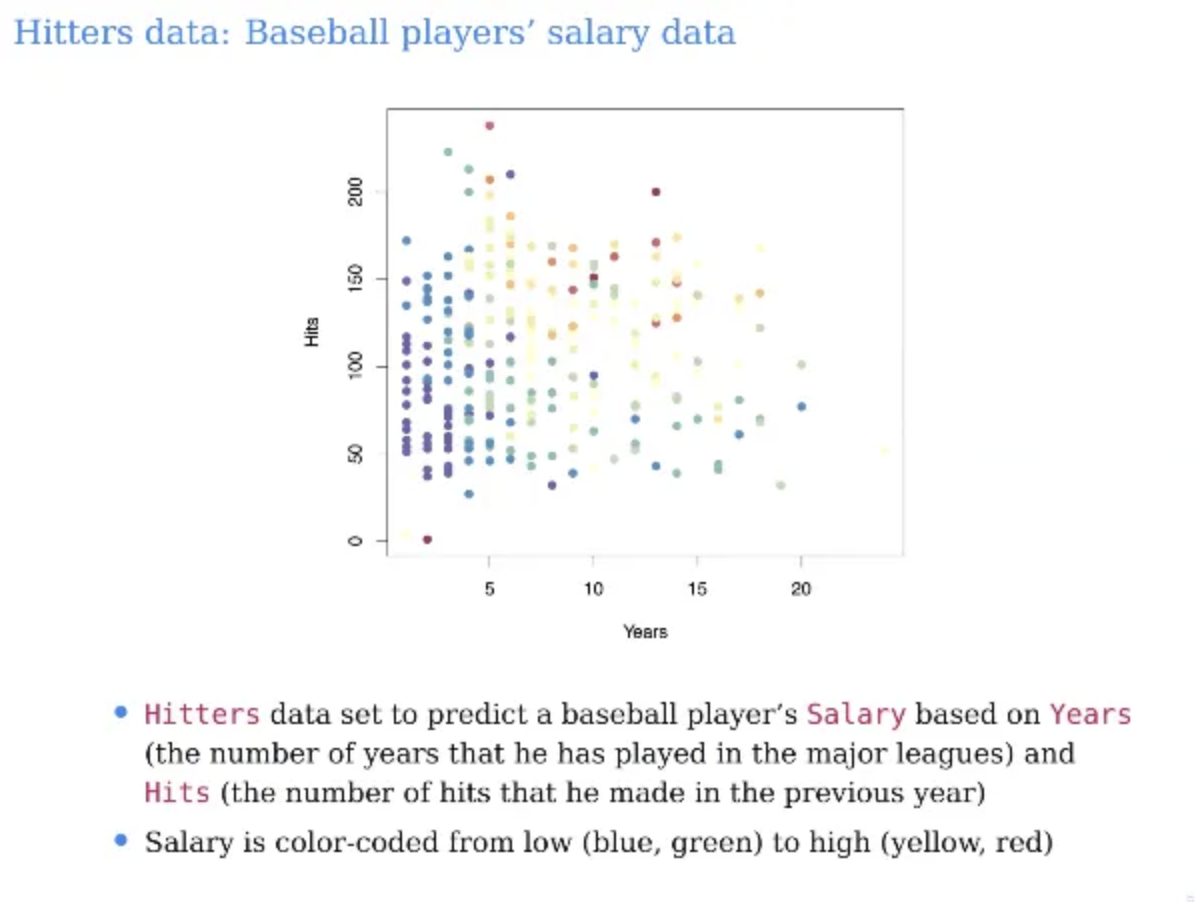
우리가 이번 시간에 예시로 들 내용은 regression problem이다
그리고 야구에서 타자의 데이터에 대한 내용이다
선수들의 경력을 나타내는 years가 x축
1년동안 안타의 개수를 나타내는 Hitts가 y축이다
각각의 데이터포인트는 선수들의 데이터 포인트이다
우리가 원하는 것은 야구선수들의 salary를 prediction하는 것이다
이 정도의 경력과 이정도의 안타수면
salary가 어느정도 되는지를 prediction하는 것이고
이건 regression problem이 된다

일단 결과부터 살펴보자
salary가 단위가 크다보니 로그를 씌워서
log salary를 예측하도록 해주었다
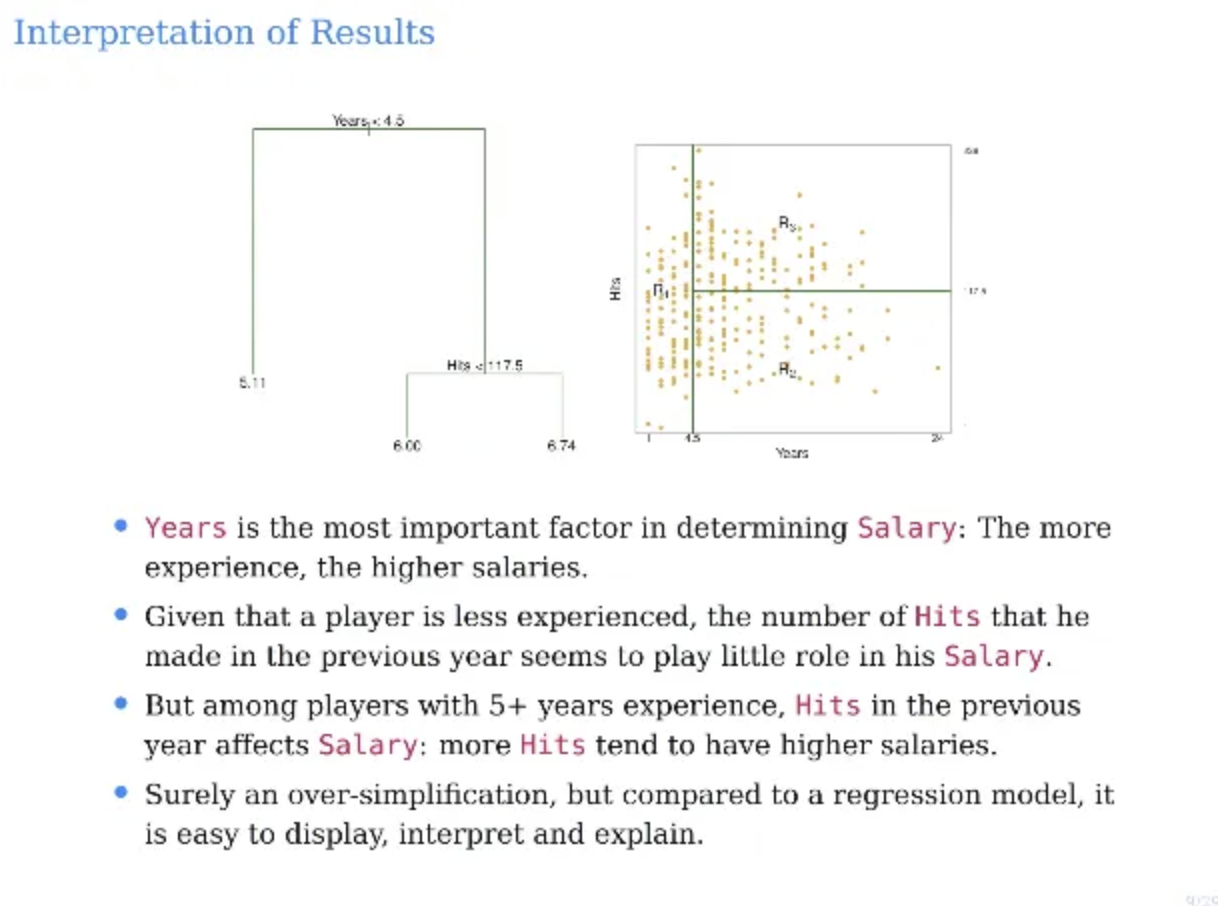
그 다음 각각의 첫 번째 decision rule은
years가 4.5년 이상인지 아닌지이다
경력이 4.5년 미만이라면 yes가 되어서 왼쪽으로 가고
아니라면 no가 되어서 오른쪽으로 가게 된다
그 다음 경력이 4.5년 이상인 사람들 중에서는
안타 개수가 117.5개를 기준으로 해서
안타가 더 많으면 salary가 더 많아지고
안타가 더 적으면 salary가 더 작아진다
이렇게 decision tree는 아주 직관적인 방식이다
아직 어떻게 나눴는지는 구체적으로 얘기는 안했지만
이 구조만 봐도 매우 직관적임을 알 수 있다
그리고 여기 끝에 있는 이 마지막 숫자들에 대해서는
트리에서 이것들을 leaves라고 부른다
그리고 가장 위는 root이다
따라서 이 문제는 hit와 years라는 variables를
어디서 자를지를 decision하는 문제이다

data space를 어떻게 segment 할 수 있을까
위는 앞에서 우리가 봤던 decision tree를 나눈 것이다
경력인 years는 4.5를 기준으로
안타개수인 hits는 117.5로 나눈 것이다
우선 첫 번째 경력 기준으로 잘랐다고 해보자
그럼 첫 번째 region이 생기는데 이게 R1이다
그런 다음 Hits를 기준으로 한 번 잘라서
2개의 region인 R2, R3가 더 생겼다
총 두번 잘랐으니까 region이 3개가 생기게 되는 것이다
그렇게 나눈 다음 prediction 값은
region에 포함되어있는 모든 데이터들의 y값의 평균값으로 한다

간단하게 용어를 살 펴보자
R1, R2, R3같은게 트리에서는 terminal node라고 부른다
그런 다음 처음 잘랐는데 terminal node가 아닌 애들을
internal node라고 부른다
위 예시에서는 internal node가 2개가 있었던 것이다
우리가 위 예시에서 years를 먼저 잘랐다
우리가 어떠한 feature를 기준으로 먼저 나눈다는 얘기는
prediction을 할 때 이 feature를 기준으로 나누는게
가장 partition이 잘 된다는 얘기이다
만약에 4.5년 이하의 경력의 야구선수라면
안타를 얼마나 많이 치던 salary는 작다는 뜻이 된다
그런데 경력이 4.5년보다 많은 야구선수라면
안타개수가 salary에 많은 영향을 준다는 뜻이다
뭐 물론 우리가 앞에서 배웠던 linear regression으로도
당연히 동일하게 수행할 수 있는데
linear regression은 feature수가 많아지면 어려워진다는 단점이 있는데
decision tree는 feature들이 아무리 늘어도 크게 영향을 받지 않는다

그렇다면 tree building을 어떻게 할까
모든 feature들 이용해서 non-overlapping
즉, partition을 하고 싶은데
어떻게든 나눠서 그 나눈 partiton 안에 있는 y값들을 가지고
prediction을 했을 때 accuracy가 좋길 바라는 것이다
이게 사실 굉장히 어려운 문제이다

그래서 개념적으로 생각해서 모든 나눌 수 있는 partition을
다 잘라본다고하면 매우 복잡해진다
그래서 보통 우리는 partition할 때 대각선 이렇게 나누지 않고
axis에 평행하게 나누는 것을 기본으로 한다
이게 아주 중요한 포인트이다
어떠한 변수를 가지고 어디서 어떻게 자를지는
항상 우리가 갖고있는 axis에 평행하게 자른다는 것이다
이렇게 되면 rectangle shape가 생기게 된다
이렇게 되면 해석이 더 용이해진다는 장점이 있다
만약 axis에 평행하게 자르지 않고 다른 방식으로도 자른다고 한다면
매우 복잡해질뿐만 아니라 해석도 어려워진다
결론적으로 우리가 최소화하고자하는 목적함수는

위 친구이다
총 J개의 Partition이 생겼고
뒤의 y^Rj값은 해당 partition에 있는 y값들의 평균이다
그래서 해당 partition에 포함된 실제 y값들의 MSE를 구했을 때
얘들을 minimize하는 박스들을 찾고싶다는 것이다
그렇다면 이걸 어떻게하면 할 수 있을까?
가능은 할까?
한 번 잘 생각해보자
만약 내가 데이터포인트가 100개가 있는데
총 10개의 partition으로 나누고 싶다고 해보자
그래서 이걸 Minimize하도록 partition을 나누고싶다
이걸 최소로 하려면 모든 space에서의 모든 구간들을 다 고려하면서 해야하는데
이렇게 되면 possible한 partition들을 다 고려해야하고
따라서 이 자체가 매우 어려운 문제이다

그래서 우리는 이 decisiont tree를 수행할 때
greedy 방식으로 수행한다
greedy 방식이란 그럼 무엇인가
현재 기준으로 그냥 가장 좋아보이는 방식을 선택하는 것이다
우리가 앞에서 subset selection에서 배웠던
stepwise 방식과 동일한 방식이다
이런걸 top-down 방식이라고도 부른다
순차적으로 우리는 predictor space를 자르면서 갈건데
한 개 자르게 되면 그게 하나의 branch가 되고
또 다음을 자르면 branch가 추가되게된다
greedy는 매번 자를 때마다
그 자른 시점에서 가장 좋아보이는걸로 새로 자른다는 의미인데
그럼 greedy하지 않은 방법은 무엇일까?
지금 기준으로는 optimal 해보이지 않는데
다음 단계에서 좋을 수도 있는 것을 선택하는 것이다
이런건 greedy한 방법이 아니다

그럼 구체적으로 어떻게 자르는지 한 번 살펴보자
우리가 자르게 되는 부분은 cutpoint라고 부른다
j는 어떤 variable에 대한 index
s는 해당 variable을 어디서 자를건지에 대한 cutpoint이다
그래서 우리가 decision을 한다는 건 무엇이냐?
j와 s가 동시에 생기는 것이다
그래서 s를 기준으로 partition하는 것이다
j와 s를 어떻게 선택하느냐에 따라서 region이 바뀌게 되는데
한 번 자를때마다 RSS가 가장 작은 점을 찾는 것이다
이 과정을 계속해서 반복한다
우리가 지금까지 본 위 예시로 한 번 봐보자
아무것도 자르지 않은 data space에서
years를 기준으로 4.5로 잘랐던게 가장 최선의 선택이었다
그래서 그렇게 잘랐다
그럼 그 상태가 되면 R1, R2 이렇게 2개의 region이 생기게 된다
그 다음 어디서 어떻게 잘라야 RSS가 가장 낮은지 정해야한다
그래서 R1이나 R2 중에서 RSS를 minimize하는 지점을 그냥 자르면 된다
그래서 그걸 찾다보니 Hitters에서 117.5가 나오게 된 것이다
그럼 첫 번째에 years를 기준으로 잘랐는데
두 번째에도 years를 기준으로 자를 수 있나?
상관없다
어디에서 어느 variable을 자를건지 결정하는 것은
이전에 어떤 variable을 잘랐는지와는 아무런 관계가 없다
어떤 해당 variable이 한 번 잘렸다고해서 다시 안잘리는게 아니다
그럼 우리가 상식적으로 한 번 생각을 해보자
그럼 상식적으로 그냥 제일 많이 자르면 RSS가 제일 낮아지는거 아닌가?
사실 당연한 이야기이다
각 region마다 데이터포인트가 1개씩 있으면
RSS는 그냥 0이 나오게 되는 것이다
하지만 이렇게 하면 training data에 대해서는 좋게 나오겠지만
결국 우리가 하고싶은건 test data에 대해서는 절대 좋을 수가 없다
따라서 이런 경우를 방지하기 위해서
대부분의 경우 stop criteria가 있다고 한다
예를 들어서 leaves에 무조건 5개 이상의 datapoint는 있어야한다라거나
tree의 depth를 무조건 5로 하겠다 등이 있다고 한다
가장 널리 쓰이는 것은 leaves size가 특정 이하로 가면 stop하는 것이라고 한다

그럼 prediction은 어떻게 하나?
test data와 같이 새로운 데이터가 들어왔을 때
예를 들어서 그 새로운 데이터 중 1개가
경력이 10년이고 안타개수가 150개라고 하자
그럼 우리가 위에서 수행한 예시에서는 R3 region에 들어가게된다
그럼 R3 region의 y값들의 평균값이 prediction 값이 되는 것이다
만약 어떤 데이터포인트는 경력이 3년이었다고하자
그럼 hit과는 관계없이 R1 region에 포함되어서
R1의 y값들의 평균값이 prediction 값이 된다
아주 간단하다
어느 partition에만 포함되는지 체크하면된다
결론적으로 정리하자면
predicted 값은 해당 partition에 들어가있는
training data의 y의 평균값들이다

위 2개 중에서 tree로 partition이 가능한 것은 무엇일까
왼쪽이 안된다는 것은 알 수 있을 것이다
순차적으로 잘랐을 때 나올 수 있는 직사각형이 아니기 때문이다
모든 partition이 다 tree로 가능한 것은 아니다
그리고 오른쪽은 우리가 순차적으로 잘랐을 때
나오는 직사각형 모양인 것을 확인할 수 있다
따라서 tree로 partition이 가능한 것은 오른쪽이다

이제 널리 사용되는 방식 중 한 개인 pruning에 대해서 알아보자
아까 위에서 설명했던 stopping criteria는 아주 보수적인 방식이다
그리고 이거 자체가 overfitting을 막는다는 보장이 없다
stopping criteria는 정말 마지노선의 룰같은 느낌이다
우리가 아까 앞에서 말했지만 사실상 최대한 많이 쪼개면
RSS를 계속해서 작게 만들 수 있다
하지만 그게 좋은게 아니라는 것을 우리는 안다
test performance가 안좋을 수 있기 때문이다
tree를 많이 쪼개지 않은 것을 작은 tree라고 하는데
bias-variance 기준으로 작은 tree는 어떻게 볼 수 있을까?
tree가 작을수록 variance는 낮아지고 bias는 커진다
반면에 모든 데이터포인트에 대해서 최대한 많이 쪼갠
large tree로 갈수록
variance는 높아지고 bias는 작아진다
split이 적을 수록 작은 tree가 되는데
이는 bias는 높고 variance가 낮다
그런데 우리가 만약 비슷한 performance라면
variance가 작은 모델을 선택하는 것이
maching learning에서의 common rule이다
또한, split 할 때마다 감소하는 RSS가 어떤 threshold 미만이면
그냥 stop하는 방법도 있다
자를때마다 RSS는 계속해서 감소하게 된다
그래서 아주 세세하게 split하면 overfit이 될 확률이 높다
그래서 우리가 잘랐을 때
RSS가 일정 threshold 이상일 때만 계속해서 자르고
그게 아니라면 그냥 멈출 수 있다
이게 아주 단순해서 좋은 방법이긴한데
short-sighted가 될 수 있다는 것이 문제다
threshold를 정해서 더 이상 자르는건 너무 RSS가 작아지니까 관두자라고 한다면
다음 번 수행에서 영향을 끼칠 수가 있따고한다
아무튼 이러한 문제 때문에 일단 threshold 없이
전체 tree를 다 grow한 다음에 pruning을 하자는 방법이 나왔다
한 마디로 일단 모든 과정을 멈추지않고 다 수행한 다음
완료된 다음 뭘 자를지를 선택하는 것이다

우리가 tree를 만들었다면 이 완성된 tree에서
어떤걸 잘라서 subtree를 찾는 이야기이다
우리가 pruning을 한다는 것은 사실
penalized된 RSS를 minimize하는 것과 동일하다

아까 decision tree의 목적함수에서 뒤에
알파 * |T|가 추가된 것을 볼 수 있다
T는 subtree의 size이고
tree의 size라는 것은 결국 leaf node의 개수가 된다
그래서 만약 어떤 tree의 leaf node가 100개가 있다면
T=100이 된다
아무튼 알파 * |T| 이 term을 추가한 것은
tree의 size가 커지는 것에 대해서 penalty를 주겠다는 의미이다
가지치기를 하지않은 가장 큰 tree가 T0이다

위의 ridge와 lasso에서 배워서 알겠지만
위 term에서 알파는 결국 penalty term과 RSS의 balance를 맞춰주는 역할을 한다
알파값이 작다면 페널티가 작아지게 되는 것이다
이러한 페널티를 추가해서 training 하는 것은 되게 일반적인 방식이다
그럼 이 적절한 알파 값은 또 어떻게 구하냐?
이건 ridge와 Lasso와 동일하게 cross-validation으로 구한다
알파값이 주어지면 그 알파값을 넣은 다음
위 식을 가장 minimize하는 것을 찾으면 된다

decision tree를 통해 regression을 수행하는 것을 요약해보자
regression tree를 Recursively하게 binary splitting을 수행해서
가장 큰 possible한 tree를 구한다
그런 다음 pruning을 apply하면 되는데
이걸 위해서 cross-validation을 통해 알파값을 구한다
그래서 결국 가장 optimal한 알파값을 찾은 다음
학습 효율화를 위해서
전체 training data에서 학습된 optimal한 subtree를 찾으면 된다

아까 위에서 말한 실제 hitter 데이터에 대한 결과이다
아까는 2개의 feature만 가지고 시각화를 했는데
그 실제 데이터는 피처들이 되게 많다고 한다
그래서 그걸 이용해서 실제로 salary를 예측했다
위는 validation set을 두지 않고 그냥 training만 시킨 결과라고한다
unpruned tree이고
아까 앞에서 말한 stop criteria만 적용시킨 것이라고 한다
이렇게 제일 처음 training만을 사용해서 큰 트리인 T0을 만든 다음에
T0부터 시작해서 알파값을 바꿔가며 여러 개의 subtree를 만든다
이 subtree들을 만들 때 cross-validation을 통해서 학습시키고
최적의 알파값을 구한다
그런 다음 최적의 알파값을 적용시켜서 모든 training data에 대해서 학습시켜서
최종 decision tree 모델을 만들어내는 것이다
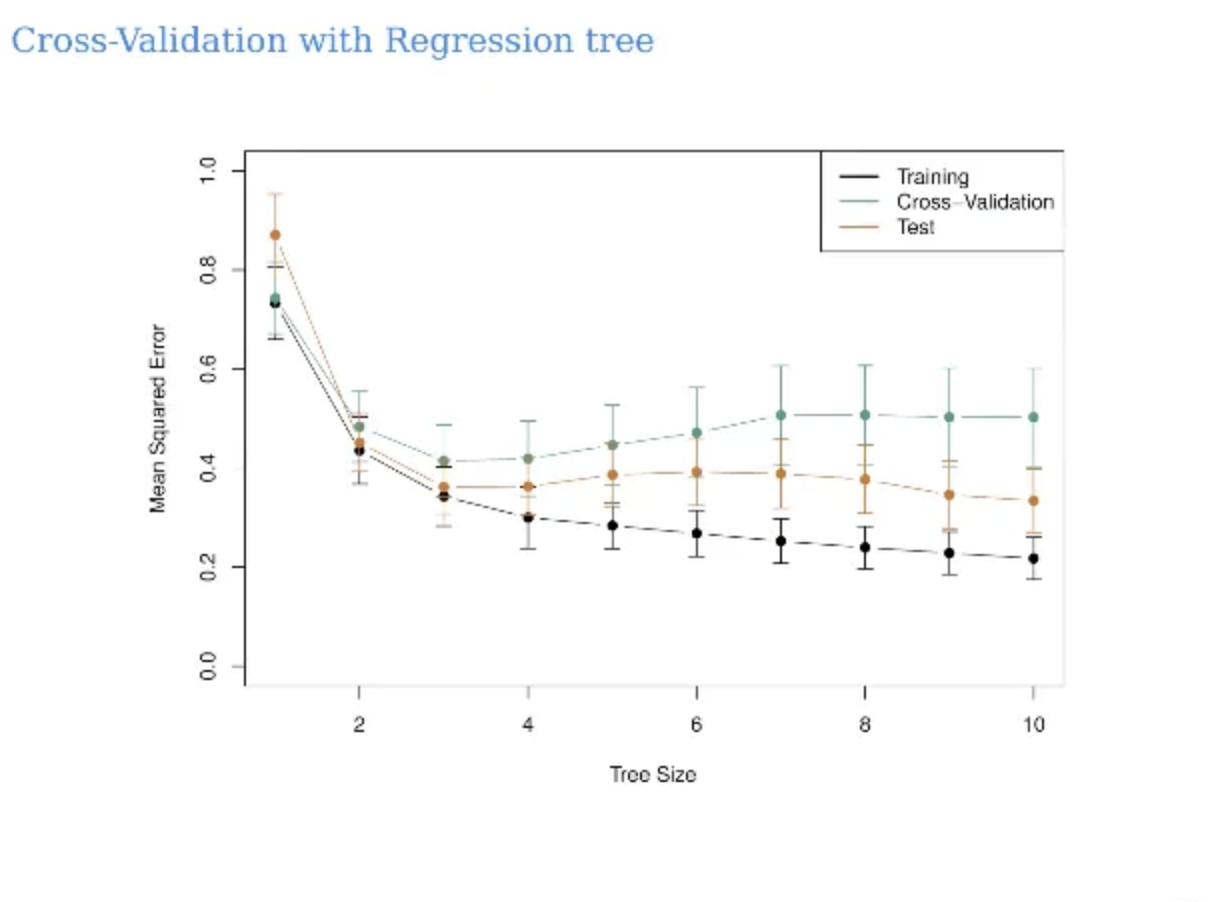
위에서 x축은 tree size이고 이건 node의 size이다
y축은 MSE 값이다
tree size의 변화에 따라서 MSE의 값을 그래프로 나타낸것이다

그럼 이제 다음으로 classification에 대해서 알아보자
y가 categorical variable인 것이다
우리가 지금까지 배운 regression과 크게 다를 것 없이 비슷하다
어느 variable을 어디서 자를건지 결정하는 것도
마찬가지로 y값을 기준으로 loss가 가장 작은 것으로 정하면 된다
어떠한 cost가 존재하는데 이걸 minimize하는 partition을 찾는 것은 똑같다
그럼 prediction은 어떻게 할까
그냥 그 partition에 속해있는 값 중에서
가장 표를 많이 받은 값이 선택되는 것이다

regression과 동일하게 recursive하게 자른다
하지만 RSS를 구할 수 없으니 classification error가 가장 작은 것으로 잘라야한다
pmk는 m이라는 region에 k class 애들이 들어가있는 propotion이다
따라서 max pmk는 그 Propotion이 가장 큰 class k의 비율값이다
즉, 1에서 max pmk값을 뺀다는 것은
해당 region에서 대표 클래스가 아닌 다른 클래스의 비율 = 오류 확률이 된다
그렇다면 E가 크다는 말은
해당 region에 class들이 많이 섞여있다는 얘기가된다
그런데 이런 classification error는
purity의 변화를 잘 캐치하지 못하기 때문에
실제로 tree-based method에서 classification error는 잘 쓰이지 않고
다른 loss를 사용한다고 한다
보통 tree에서는 gini index라는 것이 널리 쓰인다

gini index는 pmk와 1-pmk를 곱한 값을
모든 class에 대해서 다 더한 값인데
결국 m이라는 region 안에서 class들이 얼마나 고르게 있는가를 측정한다
따라서 gini index가 작다는 것은
한 개의 class가 한 개의 region에 몰려있다는 뜻이다
한 class가 독점할수록
즉, pure할수록 gini index는 작아진다
따라서 이 gini index와 함께 널리 쓰이고 있는게 cross entropy인데
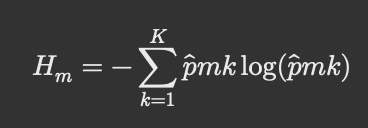
cross entropy는 위 식에서 알 수 있듯이
pmk와 log(pmk)를 곱해서 모든 class k에 대해서 더한 값이다
위 cross entropy도 class들이 한 쪽으로 쏠려야 값이 낮아진다
아무튼 그래서 gini index나 cross entropy는
numerically 굉장히 비슷한 값이고
이들은 주로 classification을 할 때 매우 많이 쓰인다고 한다

예시 데이터인 heart data를 보자
303명의 환자 데이터가 있는데
heart dieases가 있는지 없는지 binary classification을 해야하는 것이다
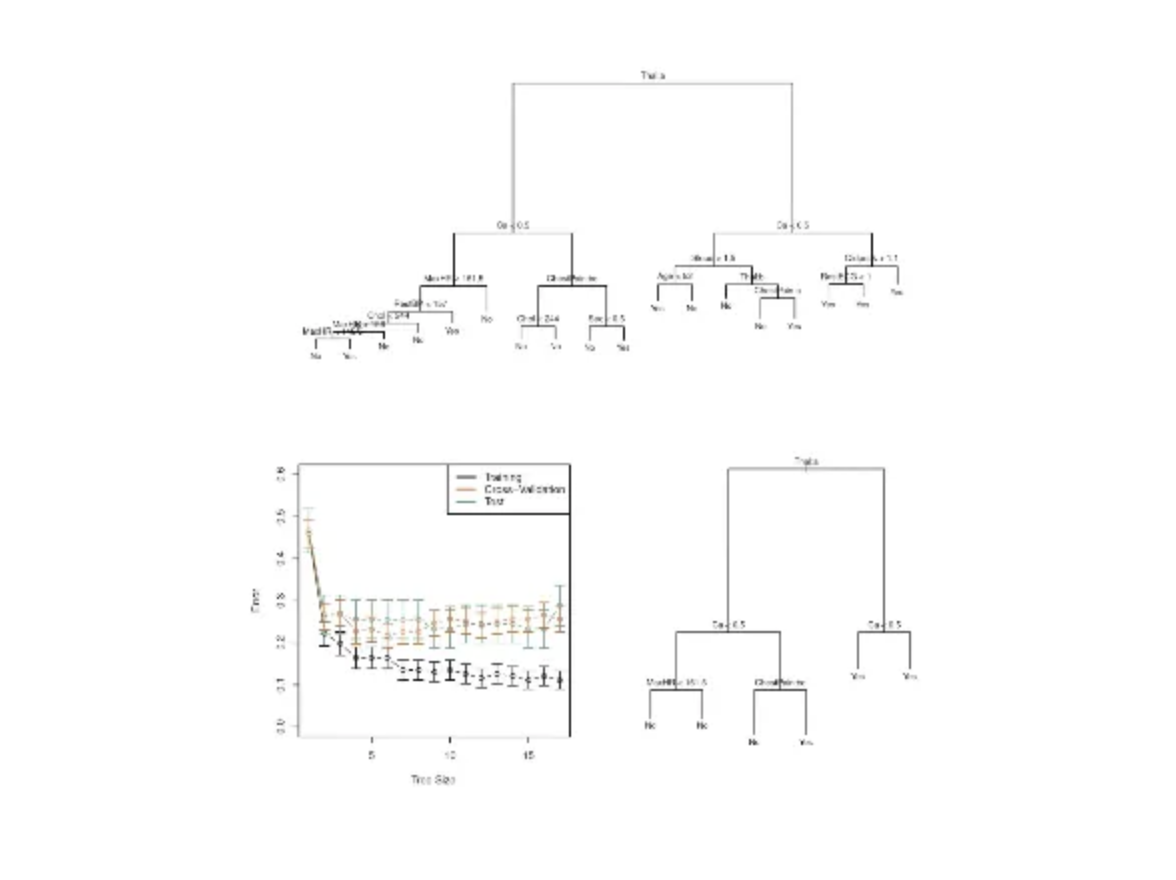
그래서 위 데이터를 가지고 classification tree를 이렇게 만들었다고한다
stop criteria만을 만족하는 T0 tree를 만든 다음
알파값을 바꿔가면서 cross-validation을 수행한 것이다
그래서 cv를 했더니 tree size가 6인 애들이 가장 좋았다고한다

x1, x2 feature가 존재하고 초록색이 1개의 class
노란색이 1개의 class라고 하자
그럼 이걸 가지고 classification을 수행하려고 하는데
linear로 수행하는 것과 tree로 수행하는 것 중 뭐가 더 좋을까?
당연히 boundary가 linear하다면 제일 첫번째 그림처럼
linear가 더 성능이 좋을 것이다
tree로 classification을 수행한다면 자르고 잘라서
어떤 게단형태처럼 생기게 될 것이다
기본적인 tree는 자를 때 axis에 평행하게 자른다
그렇기 때문에 데이터 구조에 따라서
linear가 더 적합해보일 수는 있다
저번 시간에도 얘기했지만 어떤 모델이 더 좋냐는 것은 답이 없는 질문이다
데이터가 어떤 distribution을 갖고있냐에 따라서
크게 영향을 미친다

tree-based methods들은 가장 큰 장점으로는
설명력이 매우 좋다는 것이다
그리고 우리가 배운 이런 방법이 설명이 쉬운 이유 중 한가지는
사람이 예측하는 메커니즘과 어느정도 유사한게 있기 때문이다
또 한가지 장점으로는 feature의 dimension과 상관없이
시각적으로 display히가가 좋다는 것이다
y가 continuous하건 categorical하던 다 시각화할 수 있다
하지만 단순히 이 decision tree 한 개 만으로는
SOTA급의 performance를 내기는 어렵다
따라서 다음 시간에는 조금 복잡한 tree-based model을 배워볼건데
설명력이나 단순한 점에서는 장점이 사라지기는 한다
마지막으로 decision tree의 단점으로는
robust하지 않는다는 점이 있다
데이터가 조금 바뀌는데에 있어서 partitioning이 쉽게 바뀔 수가 있는데
그게 단점일 수 있다
그래서 다음시간에는 이러한 점들을 보완할 수 있는
메소드들을 배워볼 것이다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [ML] Support Vector Machine (SVM) (0) | 2025.10.15 |
|---|---|
| [ML] Tree-based Methods 2편 (Bagging, Random Forests, Boosting) (0) | 2025.10.13 |
| [ML] Subset Selection 2편 (Shrinkage Methods: Ridge, Lasso) (1) | 2025.10.10 |
| [ML/과제 1] Linear Regression, Logistic Regression scikit-learn으로 구현하고 결과 분석하기 (0) | 2025.10.08 |
| [ML] Subset Selection 1편 (Best Subset Selection, Stepwise Selection) (0) | 2025.09.30 |