본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간에는 딥러닝의 시대가 도래하기전의 딥러닝 역할을 했던
support vector machine에 대해서 배워본다

support vector machine은 아주 멋진 방법론이라고 한다
이걸 배우면 여러가지로 classification 문제를 다룰 때의 좋은 apporach를 배울 수 있다
SVM의 목적은 binary classification이다
이 binary classification을 directly하게 하는 것인데
결국 데이터들은 어떤 feature space의 multi-diemnstion 공간에 존재한다
근데 이 공간을 어떻게 binary하게 자를까에 대한 이야기이다
그 자른다는 것은 어떤 hyperplane을 잘 feature space에 꽂아서
class들을 나눈다는 이야기이다
그런데 가끔은 데이터 자체가 binary하게 딱 seperable하지 않을 때도 있다
그래서 이런 경우에는 그 데이터를 seperate할 때 조금 더 느슨하게(relax) 할 수 있다
feature space 자체를 더 high dimension을 높인 다음에 seperate하는 방법인데
이것도 뒤에서 배워볼 방법이다

그렇다면 우선 hyperplane이 뭔지부터 배워보자
linear regression을 할 때부터 hyperplane이라는 말이 나왔는데
hyperplane이란 아주 단순하게 설명하면
p-dimensional space에서 p-1 dimensional의 flat한 subspace를 의미한다
여기서는 affine subspace라고 부르는데
우리가 linear algebra 시간에 배웠던 subspace는 원점을 지나야하는데(originate)
affine subspace는 원점(origin)을 지나지않고 조금 떨어져있다
아주 쉽게 2차원의 우리가 흔히 아는 좌표평면을 예시로 들어보자
이 2차원의 좌표평면을 binary로 나누는 hyperplane이 필요하다
그러려면 이 hyperplane은 그냥 단순한 line이 될 것이다
2차원의 평면이기 때문이 1차원의 선이 hyperplane이 되는 것이고
이 선이 반드시 원점을 지날 필요는 없다
이러한 hyperplane은 수식으로 나타내면 아래처럼 나타낼 수 있다

X들은 variable들이고
hyperplane의 기울기를 결정하는 요소는 베타들이다
베타0이 결국에는 offset이 얼마인지를 결정짓는 요소가 된다
즉 베타0이 0이면 이 hyperplane은 origin을 지나게 된다
위 식에서 베타0을 제외한 베타1부터 베타p까지를 뽑아낸게
normal vector(법선 벡터)이다
이런 normal vector는 방향이 굉장히 중요한 벡터이고
이 normal vector는 hyperplane에 무조건 orthogonal하다

예시를 한 번 보자
2차원의 좌표평면에서의 hyperplane이 위와 같다고 하자
위 hyperplane은 1+2X1+3X2=0이다
그렇다면 여기서 normal vector는 (2, 3)이 된다
위에서 보면 hyperplane을 기준으로 오른쪽은 파란색이고 왼쪽은 보라색이다
이는 hyperplane에서 function값이 양수면 오른쪽, 음수면 왼쪽이다
그럼 위 hyperplane 위에 있는 점들은? 0이 된다

그래서 결국 우리가 오늘 배울 SVM은
seperating hyperplane을 찾는 것이다
위 예시를 한 번 살펴보자
이 2차원 feature space에 2차원 데이터들이 존재한다
blue class와 purple class가 존재하고
따라서 이 데이터들을 blue와 purple로 나눌 수 있는
hyperplane을 찾고싶은 것이다
그런데 왼쪽의 그림같은 경우
3개의 hyperplane 모두 blue와 purple class를 잘 나눠준다
위 3개의 hyperplane 뿐만이 아니라
사실 두 클래스를 나눌 수 있는 Hyperplane은 infinity many이다
사실 데이터가 linearly seperable 여러 개의 hyperplane이 존재할 수 있는데
그럼 그중에서 가장 좋은 hyperplane은 어떻게 찾을 수 있을까?

데이터를 binary하게 seperate하는 hyperplane 중에서
가장 좋은 것은 margin이 가장 큰 hyperplane이다
우리가 hyperplane을 찾으면 거기 기준으로
양쪽의 margin을 가장 넓히고 싶은 것이다
한 마디로, training data 기준으로 fit을 잘한다는 것은
그 중에서도 margin이 제일 큰 seperate hyperplane을 찾는 것이다

위 식에서 M이 나타내는 것은 margin이다
optimization 문제를 볼 때, maximize나 minimize를 다루는 것은
objective function이라고 하는데
위 식처럼 subject to라고 하는건 constraint 문제이다
왜냐면 아래의 constraint를 만족하는 solution들 중에서
이 M값을 찾을 것이기 때문이다
그렇다면 우선 첫 번째 constraint를 보자
첫 번째 constraint는 모든 베타값들의 square summation이 1이 되어야한다
이게 무슨 뜻이냐? 잘 생각해보자
이 normal vector의 길이는 1로 정해져있고
여기서 방향만 정해준다는 뜻이 된다
두 번째 constraint를 잘 보자
괄호안의 식은 hyperplane이고
i는 각 data observation들이다
각각의 observation 기준으로 hyperplane 식에 집어넣으면
양수 혹은 음수가 나오게 된다
위 예시에서 파란색 부분이 양수인 hyperplane이라고 하자
그럼 파란색의 데이터포인트를 식에 넣으면 hyperplane은 양수가 나온다
그리고 파란색이면 양수이기 때문에 yi도 양수가 나오게 된다
그럼 파란색 데이터포인트를 넣었을 때 yi * hyperplane은 양수가 된다
그렇다면 빨간색 데이터포인트를 넣었을 때를 살펴보자
빨간색 데이터포인트를 넣었을떄 hyperplane 값도 음수가 되고
yi값도 음수가 된다
그래서 이 둘을 곱하면 결국 양수가 된다
따라서 어느 side에 있던지 Hyperplane을 기준으로
correct side에 있으면 무조건 양수값이 나오게 된다
따라서 양쪽 사이드에 있는 데이터들을 우리가 classify하고
hyperplane과 Margin을 가장 크게 만드는 식이 위 식인 것이다

다시 한 번 위 optimization 식을 살펴보며 정리해보자
가장 마지막 3번째 constraint는 앞에서도 설명했지만
M이 0보다 크다 = 양수라고 하면
모든 데이터포인트들이 모두 correctly하게 correct side에 있다는 뜻이다
두번째 constraint에서는 베타 제곱의 합을 정확히 1로 두는데
여기서 왜 1인지는 중요하지 않다
중요한 것은 베타 제곱의 합을 어떤 숫자로 고정시켰다는 것인데
이는 베타값을 이용해서 방향만 정해주겠다는 의미이다
이걸 1로 설정한 이유를 간단하게 설정하자면
어떤 점 xi가 hyperplane으로부터 떨어져있을 때
얼마나 떨어져있는지를 재는 perpendicular distance는
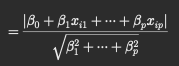
위와 같은 식으로 나타낼 수 있다
그런데 분모가 베타1부터 p까지의 제곱의 합인 것을 알 수 있다
그럼 이걸 1로 설정하면 사실상 분모는 그냥 사라지고
perpendicular distance는 그냥 분자값이 되는데
이 분자값은 hyperplane과 동일하다
따라서 베타 제곱 summation을 1로 두면
hyperplane의 저 식이 정확하게 hyperplane에서 i번째 observation까지의
perpendicular distance를 의미하게 되는 것이다
따라서 computation 관점에서 편해지기때문에 1로 설정해준다고한다
하지만 더 중요한 것은 normal vector의 방향만 정해주면 된다는 것이다
아무튼 2번과 3번 constraint가 모두 함께 있어야
각각의 데이터포인트들이 hyperplane 기준으로 correctly하게 위치하면서
M만큼의 margin을 두는데 이 M을 maximize 시킬 수 있는 것이다
그리고 결국 우리가 이를 수행하기 위해 건드려야하는 것은 베타값들이다
베타들을 어떤 방향으로해서 hyperplane을 찾아서
이 margin을 최대화시킬 수 있는지가 SVM을 해결하는 문제이다
굉장히 수학적으로 아름다운(?) 문제라서
연구자들이 아주 활발하게 연구한 방법론이라고 한다
또한 이것도 generalize하기 좋은 부분이 있어서
현업에서도 많이 사용하고 있다고 한다

지금까지는 우리가 linearly seperable 할 때만 가정했다
즉, 데이터들이 직선만으로 완전히 구분이 가능할때만 가정했다는 뜻이다
그런데 만약 그렇지 않다면?
위 예시를 한 번 살펴보자
그냥 직선으로는 두 데이터 class를 완전하게 구분할 수가 없다
이런걸 linearly seperable하지 않다고 말한다
보통 데이터포인트의 개수 n이 dimension의 개수 p보다 작을 때 발생하고
그렇지않을 때도 종종 발생한다

또 이런 경우도 있을 수 있다
데이터가 seperable 할 수는 있는데
데이터에 noise가 있을 수가 있다
SVM은 데이터가 boundary 근처에서 많이 변한다면
hyperplain이 확확 변할 수가 있다
위 예시에서도 확인할 수 있다
원래는 왼쪽처럼 maximum margin으로 boundary를 생성했는데
경계 근처에 새로운 파란색 데이터포인트가 딱 1개 생겼다
그래서 boundary가 많이 바뀐 것을 확인할 수 있다
이 말이 무엇이냐하면 classifier의 variance가 크다는 뜻이다
그래서 이러한 위의 단점들
noise 데이터나 linearly seperable하지 않는
이러한 단점들을 극복하기 위해서
soft margin을 활용한 SVM을 배워보자

soft margin이라는 것은 margin에서 어느정도의 violation을 허용하는 것을 말한다
위 식을 한 번 잘 살펴보자
앞의 식이랑 나머지는 다 똑같은데

위 부분에서 M에

이 식이 곱해져있는 것을 확인할 수 있다
저기서 저 친구를 slack variable이라고 하는데
slack variable은 반드시 양수이다
그럼 이게 양수란 것은 어떤 뜻일까?
그럼 만약에 저 slack variable이 0과 1사이의 양수라고 해보자
그럼 1에서 이 slack variable을 뺀 값을 M에 곱하기 때문에
M값, 즉 마진을 축소시킨다는 것을 알 수 있다
그럼 그 축소시킨 값만큼 해당 데이터포인트는 마진을 조금 더 넘어서도 되는 것이다
위에서 예시를 한 번 살펴보자
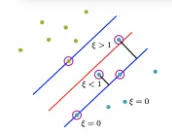
위 예시에서 빨간색 실선이 boundary이고
파란색까지가 margin의 거리이다
파란색 선 위에 있는 푸른 데이터포인트들은
slack variable이 0인 값들이다
그런데 그 위에있는 slack variable이 1보다 작은 푸른 데이터포인트를 살펴보자
이건 slack variable이 1이기 때문에 boundary보다는 안에 있지만
실제 margin보다는 작은 것을 확인할 수 있다
그런데 반면에 boundary를 넘어간 slack variable이
1보다 큰 저 푸른색 데이터포인트를 잘 살펴보자
이 친구는 푸른색 class이기 때문에 빨간 boundary의 오른쪽에 와야함에도 불구하고
왼쪽으로 가있는 모습을 볼 수 있다
이런 경우 slack variable이 1보다 큰 경우이고
그럼 마이너스가 되는 것이다
음수가 된다는 것은 correct 하게 분류되지 않았다는 뜻이다
하지만 soft하게 해서 이런것들까지 허용을 한다는 의미이다
그런데 이걸 한없이 허용해줄 수는 없다
그렇기 때문에 이 허용치인 slack variable에 bound를 정한다
따라서 보통 그 허용치를 C로 두고

위와 같은 constraint를 둔다
모든 데이터포인트들에 사용된 slack variable의 합이
C보다 작아야한다
그래서 이 C를 보통 budget이라고 부른다
그런데 여기서 질문이 들어왔다
그냥 SVM에서 boundary를 결정하는데 있어서
어떤 데이터포인트들이 영향을 줄 수 있을까?
위 예시에서 margin을 결정짓는 것은 딱 5개이고
나머지 데이터포인트들은 영향을 미치지 않는다
이게 바로 SVM에서 굉장히 재미있는 부분이라고 하는데
데이터포인트가 얼마나 많던간에 이 margin을 결정짓게 하는 애들을
support vector라고 부른다
그럼 단순하게 생각해서 저 support vector만 찾으면 되는거아니냐? 할 수 있겠지만
이건 결과론적인 것이다
margin을 찾고나서야 얘네가 support vector였구나! 라는 것을 알 수 있는 것이다
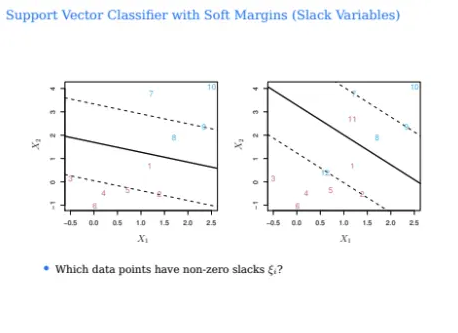
그럼 이 예시를 한 번 잘 살펴보자
지금 위 데이터포인트들에서 slack variable이 0이 아닌 것은 무엇인가?
왼쪽의 경우는 파란색 class의 경우 8
그리고 빨간색 class의 경우 1이 될 것이다
오른쪽의 경우 파란색 class의 경우 8, 12이고
빨간색 class의 경우 1, 11이다

아까 그러면 C가 slack variable을 얼만큼 허용할지를
결정해주는 것이라고 했다
그렇다면 C의 의미를 한 번 생각해보자
C가 크다면 margin이 넓어질까? 작아질까?
위 4개 중에서 C가 가장 큰건 어떤 것일까?
당연히 1번이다
C가 크다는건 그만큼 violation을 많이 허용한다는 의미이고
그럼 margin이 커지게 된다
C가 작아지면서 천천히 1->2->3->4 순으로 가게 되는 것이다
그래서 C에 따라서 support vector도 달라지고
C에 따라서 hyperplain도 달라진다
그럼 적절한 C값은 어떻게 찾을까?
그건 늘 그렇듯 cross-validation으로..
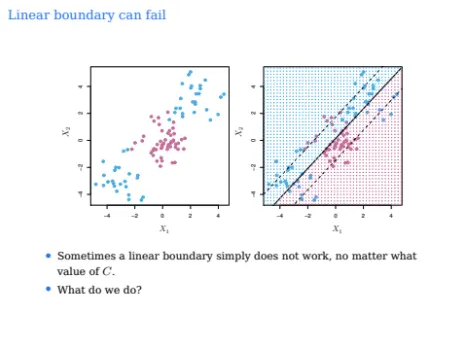
우리가 위에서 배운건 약간의 violation을 허용해서
linearly seperable하도록 만든 것이었다
하지만 아무리 violation을 해도 linearly seperable하지 않다면?
위 예시를 한 번 잘 살펴보자
그 어떤 slack을 허용하더라도 linear하게는 seperable하지 못하다
C를 아무리 넓히고 키워도 불가능하다
이런 경우는 어떻게 해야할까?

확실히 non-linear하게 구분할 수 있는 것이 필요하다
그래서 SVM에서는 kernel을 사용한다
물론 kernel은 SVM에서만 쓰이는 것은 아닌데
일단 kernel에 대해서 잠깐 배워보자

우선 inner product의 개념부터 살펴보자
xi와 xi'라는 2개의 p차원 벡터가 있다고 해보자
p차원의 두 벡터를 그냥 element-wise multiplication 한 다음에
sum한 것을
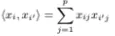
위와 같이 define 할 수 있다고 해보자
그렇다면 우리가 지금까지 배웠던 linear support vector는

위와 같이 나타낼 수가 있다
위 식에 대한 내용은 여기서는 자세하게는 다루지 않겠지만
아무튼 이렇게 나타낼 수 있고 n개의 알파라는 파라미터가 존재하게 된다

식에 대한 간략한 설명은 위 gpt의 설명을 참고하면 좋을 것 같아 가져와봤다
아무튼 위에서 말했지만 SVM의 결과에
모든 데이터포인트가 다 영향을 미치지는 않는다
그래서 그 영향을 미치지 않는 애들은 영향력의 가중치인 알파가
0이 되는 것이다
그렇다면 알파가 0이 아닌 애들이 SVM을 결정하는
support vector가 되는 것이다

그럼 위 예시에서 알파가 0보다 큰 값은 무엇일까?
왼쪽같은 경우는 파란색은 8, 9이고 빨간색은 1, 2가 될 것이다
오른쪽같은 경우는 파란색은 8, 9, 10, 12가 빨간색은 1, 2, 11이 될 것이다
아무튼 support vector들의 집합을 support set이라고 하는데
inner product를 기준으로 하면 알파를 보고
어떤 것이 support set인지 알 수 있다

위에서 kernel을 설명하기위해 Inner product의 예시를 들었지만
inner product는 linear SVM을 할 때 사용하는 것이다
그럼 우리는 아까부터 계속 non-linear SVM을 kernel을 이용해서 수행하자고했다
그래서 이번에는 non-linear SVM을 다루는 kernel들에 대해서 배워보자
첫 번째 예시로는 polynomial kernel이 있다
식은
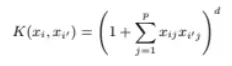
위와 같이 생겼는데 inner product에서 조금 변형된 식이다
아무튼 inner product에서 d제곱을 한 것과 유사한 형태인데
d가 더 높아질수록 inner product보다 더욱 flexible한 function이 생긴다
그걸 가지고 우리는 더욱 flexible한 classifier를 만들 수 있다

위 gpt의 설명을 보태면 더욱 이해하기 좋을 것 같다
아무튼 이러한 polynomial kernel을 통해서
아까처럼 SVM을 표현하면

위와 같이 표현할 수 있다
여기서 kernel K는 inner product가 아니고 polynomial이다
하지만 아까 linear SVM과 동일하게
알파^이 0보다 큰게 support set이 되고
알파^이 0인 애들은 classifier에 기여하지 않는 것이다
또한 이 경우 d도 파라미터에 해당한다
그래서 여기서 우리가 estimate하고 싶은 것은 결국 무엇이냐?
알파와 베타0을 찾고 싶은 것이다
그럼 데이터를 구분하는 classifier를 찾을 수 있는 것이다

그 다음으로는 Radial Kernel에 대해서 살펴보자
가장 널리 쓰이는 커널 중 하나이다
xi, xi'가 모두 p차원의 벡터들이고
이 두 벡터들이 얼만큼 떨어져있느냐에 감마값을 곱해준 다음
이를 exp한 것이다
감마는 튜닝 파라미터가 된다

만약 이 두 벡터가 가까이 있다면 어떻게 될까?
두 벡터가 exactly same이면 뒤의 제곱값은 0이 될 것이고
distance가 점점 커지면 커질수록 제곱값은 커지는데
커널의 전체 값은 지수함수 0에 가까워진다
반면에 두 distance가 작을수록 제곱값은 작아지지만
커널의 전체 값은 지수함수에서 1에 가까워진다
그럼 이게 무엇을 의미하냐?
데이터포인트들이 가까우면 커널 값이 커지고
데이터포인트들이 멀면 커널 값이 작아진다
따라서 멀리 있는 점들을 classifier에 영향을 덜 미치게 해주고
가까이 있는 점들은 더욱 영향을 미치게 해주고싶은 것이다
그래서 radial kernel은 local behavior가 굉장히 잘 드러나는데
어느정도로 먼 데이터포인트까지 영향을 미칠 것인지를
컨트롤 해주는 것이 바로 감마 값이다
따라서 만약 감마값이 작다면 거리가 멀어질 때마다 커널이 천천히 감소해서
멀리 있는 데이터포인트들도 고려하게 되는 것이다
이렇게 되면 decision boundary는 좀 더 smooth해진다
왜냐면 더 많은 데이터포인트들을 이용해서 classify를 수행하기 때문이다
반면에 감마값이 크다면?
거리가 멀어질때마다 커널값이 빠르게 줄어들어서
가까이 있는 데이터포인트들 위주로 classify 하게 된다
따라서 더 작은 개수의 데이터포인트들로 classify를 하기 때문에
boundary가 좀 더 wiggly해지게 된다

교수님 설명만으로 부족해서 gpt와 같이 공부를 하고있는데
참고하면 좋을 것 같다

그럼 이제 위에서 배운 두가지 non-linear kernel인
polynomial과 radial kernel을 비교해보자
왼쪽이 polynomial이고 오른쪽이 radial이다
왼쪽은 polynomial에서 d=3으로 수행한 결과이다
아까 위 데이터는 linearly seperable하지 않은 데이터였는데
이렇게 polynomial SVM이나 radial SVM으로는 가능하다
여기서 점선은 margin을 의미한다

경계에서 조금 벗어난 데이터들에 대해서는
soft margin이 적용된거냐고 물어봤더니
그렇다고한다

Heart Data로 SVM과 LDA의 성능을
ROC curve를 이용해서 비교해보자
ROC curve는 이전에 배웠는데
뾰족하면 뾰족할수록 performance가 좋은 것이라고 했다
왼쪽을 보면 LDA와 SVM을 비교하는데
SVM이 조금 더 성능이 좋아보인다
여기서는 linear SVM을 사용한 것이라고 한다
오른쪽은 빨간색은 똑같이 linear SVM인데
나머지가 radial kernel을 사용한 SVM이라고 한다
각 감마값들이 색깔별로 구분되어있다
위를 보면 감마값이 큰게 가장 성능이 좋은 것을 알 수 있다
거의 직각모양이 되어있다
감마값이 클수록 가까운 데이터포인트들만 고려하기때문에
decision boundary가 더 wiggly해진다
그래서 퍼포먼스가 이정도로 잘나온 것을 확인할 수 있는데
이게 training data에서 측정한 것이기 때문에
overfitting을 의심해봐도 좋을 것 같다
하지만 이 ROC curve만 보고서는 overfitting이라고 확신할 수는 없다

이제 test data에서 측정한 결과를 보자
SVM과 LDA를 비교한 왼쪽을 봤을 때
확실히 test에서도 SVM이 더 좋은 것을 확인할 수 있다
그런데 오른쪽에서는 다들 큰 차이가 없이 비슷비슷한 것을 볼 수 있다
그리고 감마값이 가장 큰것에 대해서 위 training data에서 측정한 것과 비교해봤을 때
성능차이가 제법 많이 나는 것을 확인할 수 있다
따라서 감마값을 너무 크게 잡으면 overfitting이 발생할 수도 있다는 것을
유념해두면 좋을 것 같다
따라서 가장 적정한 감마값을 선택할 때는
cross-validation을 사용하는 것이 가장 좋다

그럼 지금까지 binary classification을 수행하는 SVM만 배웠는데
만약 class가 2개보다 많다면 어떻게 될까?
이걸 수행할 수는 있는데
binary에서 한 것처럼 principle한 방법은 아니고
heuristic한 방법으로 수행할 수 있다고 한다
총 2가지 방법이 있는데
One Versus All(OVA)와 One Versus One(OVO)가 존재한다
먼저 OVA부터 살펴보자
이건 이름 그대로 하나의 클래스 vs 나머지 전체 클래스로 분류기를 만드는 것이다
예를 들어서 클래스가 A, B, C 3개라고 한다면
1. A vs B+C
2. B vs A+C
3. C vs A+B
이렇게 3개만큼 SVM 학습을 시킨다
그렇다면 K개의 class에 대해 학습시킨다면
총 K개의 SVM이 나오게 된다
그런 다음 새로운 데이터포인트가 들어오면
각 SVM에 넣어본다음 가장 큰 값을 assign 해주는 것이다
그럼 두 번째로 OVO를 살펴보자
이름 그대로 클래스별로 하나씩 비교하는 방법이다
A, B, C 클래스가 있다고 하면
1. A vs B
2. A vs C
3. B vs C
이렇게 각각 비교하는 방법이다
따라서 총 SVM의 개수는 KC2개의 조합이 나오게 된다
이것도 동일하게 새로운 데이터포인트가 들어왔을 때
각각의 SVM에 다 넣은 뒤 가장 많이 나온 애를 assign 시키게 된다
그럼 위 2가지 OVA, OVO 중에서 어떤걸 쓰는게 좋을까?
단순히 계산량만 보면 OVA가 더 나아보일 수 있지만
K가 그렇게 크지 않다면 OVO가 더 낫다고 한다
그 이유는 OVA의 경우 데이터의 형평성 문제가 발생할 수 있기 때문이다
각 SVM마다 한개의 클래스 vs 나머지 전체 이렇게 학습시키기 때문에
데이터간의 Imbalance가 생겨 데이터의 경계가 왜곡될 수가 있다
그리고 또한 데이터가 Multimodal이 될 확률이 큰데
다른 deep learning에서 말하는 multimodal이 아닌
distribution에서 말하는 "여러 개의 분포를 가진 봉우리"라는 뜻의 multimodal이다
그래서 SVM이 더욱 명확하게 데이터를 분리하기 어려워진다
따라서 K가 작다면 OVO로 하는 경우가 더 유리하다고 한다


gpt는 비유를 참 잘해준다

이제 SVM과 logistic regression을 비교해보고 오늘 공부를 마쳐보자
linear SVM은 위와 같이 hinge loss로 loss function을 설정한다

Hinge Loss는 위와 같다
따라서 위 ppt에서는 SVM의 검정 선이 hinge loss라고 할 수 있다
그런데 이 hinge loss는 logistic regression에서
ridge penalty를 한 것과 매우 유사하다
따라서 결국 저 끝에서 logistic regression은 0에 가까이 가지만
정확하게 0은 되지 못한다
하지만 SVM은 정확하게 0으로 떨어지게 된다
사실 SVM과 logistic regression은 2개의 behavior가 비슷하지만
마지막 부분 때문에 달라지게 되는 것이다

우리가 앞에 logistic regression을 배웠을 때
logistic regression에서는 class들이 well-seperate 된 경우
오히려 더 variance가 클 수 있다
데이터포인트들이 잘 seperate 되어있으면 상식적으로라면
잘 classify 되어야하는데
logistic regression에서의 그 curve를 가운데에서
어느정도로 완만해야할지 가파르게해야할지를 계산을 못하는 것이다
하지만 SVM은 그런거에는 전혀 상관이 없고
데이터가 well-seperate 되어있을수록 퍼포먼스가 굉장히 좋다
그런데 데이터들이 Overlapping이 되어있는 경우에는 logistic regression이 더 유리하다
하지만 가장 중요한건 logistic regression은 확률을 구할 수 있다는 것이다
SVM은 확률값이 나오지는 않는다
또한 boundary 자체가 non-linear 한 것을 찾으려고 한다면
kernel SVM을 사용하면 좋을 것이다
사실 SVM을 어렵게 배우려면 굉장히 어렵게 배울 수 있다
하지만 이 SVM을 왜 수행하는 것인지
이걸 배우는 목적이 무엇인지
non-linear이 무엇인지를 정확하게 이해한다면 좋을 것 같다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [ML] Clustering (k-means clustering, hierarchical clustering) (0) | 2025.10.27 |
|---|---|
| [ML] Principle Components Analysis (PCA) (0) | 2025.10.17 |
| [ML] Tree-based Methods 2편 (Bagging, Random Forests, Boosting) (0) | 2025.10.13 |
| [ML] Tree-based Methods 1편 (Decision Trees) (1) | 2025.10.12 |
| [ML] Subset Selection 2편 (Shrinkage Methods: Ridge, Lasso) (1) | 2025.10.10 |