본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다
오늘은 중간고사 후 머신러닝의 마지막 시간
clustering에 대해서 배운다
다음 시간부터는 딥러닝 내용으로 넘어간다

cluserting에 대해서 살펴보자

clustering이란 데이터포인들이 있으면 이들을 어떻게 subgroup으로
나눌건지에 대한 내용이다
한 마디로 데이터포인트들을 partition으로 나누는 것이다
데이터들은 x가 존재하고 y는 있을수도있고 없을 수도 있는데
clustering도 unsupervised learning이기 때문에 y를 신경쓰지않는다
오직 x feature만 보고 clustering을 수행한다
그런데 어떤 데이터들이 가까운지 비슷한지 다른지에 대해서
명확한 기준이 unsupervised learning에서는 존재하지 않는다
따라서 정답이 없다는 뜻이다
그래서 내가 가진 도메인 지식 안에서 비슷하다는 개념은
어떤 것인지를 정의해야하는 경우가 있다

이전 시간에서 배웠던 PCA와 잠깐 비교해보자
PCA와 clustering은 비지도학습의 대표적인 방법이다
PCA는 데이터의 차원을 축소가호 싶을 때
데이터 안의 variance를 최대한 보존하면서
어떻게하면 low dimension으로 나타낼 수 있을까인데
clustering은 dimension reduction이나 variance를 유지하는 그런 질문은 아니다
clustering은 데이터들을 묶을 때 어떻게하면 최대한 비슷한 것들끼리 묶고
다른 것들은 어떻게하면 최대한 떨어뜨릴까에 관한 것이다

우리는 총 2가지의 clustering 방법론에 대해 배울 것인데
첫번째가 k-means clustering이고 두 번째가 hierarchical clustering이다
k-means에서 k는 총 몇 개의 subgroup으로 나눌 것인지이다
따라서 k=subgroup 숫자가 된다
그리고 hierarchical clustering은 클러스터링 subgroup의 숫자를 사전에 정하지 않고
데이터들을 merge하면서 tree모양의 구조를 만든 다음
사후에 어떻게 할지 정하는 것이다

우선 k-means clustering부터 살펴보자
clustering에서 가장 대중적이고 가장 단순한 알고리즘이다
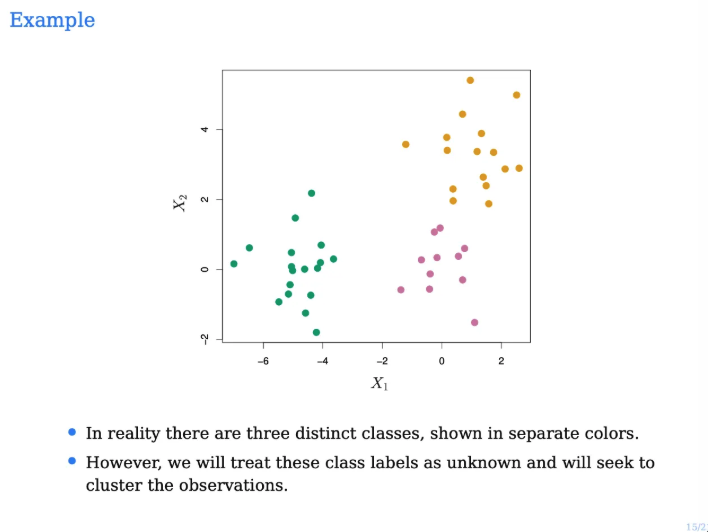
위 예시에서는 k들을 각각 다른 값으로 설정한 것이다
위 예시에서 색깔이 의미하는 것은 없다
그냥 색이 다르다는 것은 다른 cluster구나 정도로만 이해하면 좋다
그리고 unsupervised learning이기 때문에
해당 점들의 true clsuter는 존재하지 않는다
위 예시를 우리가 시각화 할 수 있는 이유는
feature space가 2 dimension이기 때문이다

C1, C2, ..., Ck는 모두 index set이다
데이터포인트들이 첫 번째 cluster에 들어갔다고 하는 것은
C1에 있다고 하는 것이다
두번째에 들어간 데이터들의 index는 C2에 위치한다
그리고 마지막 k번쨰 cluster에 들어간 데이터포인트들의 index는 Ck이다
총 데이터포인트의 개수는 n개라고 하면
저 cluster들을 다 합집합으로 만들면 전체 데이터 n개를 다 커버해야한다
즉 어디에도 속하지않는 데이터가 있으면 안되며
클러스터들끼리 교집합은 반드시 공집합이어야한다
즉, overlap이 없는 partition이어야한다

그렇다면 k-means는 어떻게 목적함수를 설정할까
k-means는 within-cluster variation(WCV)를 사용한다
small K번째 clsuter안에 들어가있는 각각의 데이터포인트들이
그 안에서의 variance가(cluster 내의 variance가) 작았으면 좋겠는 것이다
따라서 모든 clsuter들의 variance들의 합을 최소화하는 것이다
이렇게 하다보면 각 cluster끼리는 자연스럽게 떨어져있게된다
따라서 WCV의 summation을 최소화하는 것이 가장 이상적이다

따라서 WCV를 한 번 살펴보자
위의 예시는 유클리드거리를 기준으로 한다
k번째 클러스터에 들어가있는 WCV를 구해보자
k번쨰 cluster에 들어가있는 데이터포인트들만 뽑아서
그 애들의 각각의 Feature를 기준으로 차를 구한 다음에 제곱한다
i번째 데이터포인트들의 feature가 1부터 p까지 있으면
k cluster안에 있는 i번째랑 i'번째의 데이터들을 pair-wise로 거리를 구한다
그래서 모든 클러스터에서 이 값을 합친 값이 작았으면 좋겠는 것이다
그래서
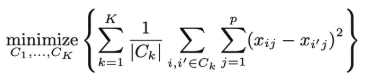
이를 위와 같은 수식으로 표현하는데 여기서 우리가 조정할 수 있는 것은
cluster assignment이다
따라서 우리가 이 cluster assignment를 조정하면서
이걸 조정해서 만들어지는 WCV의 summation이 가장 최소화되었으면 좋겠는 것이다

이제 그럼 알고리즘을 살펴보자
가장 처음에는 각각의 데이터포인트들에 cluster를 randomly assign한다
이 전에 k를 몇 개할지를 먼저 정하는데 k는 Input 값이다
만약 k=5라고 가정해보자
각각의 데이터포인트들에 걍 uniformly random하게 assign한다
이건 아무 의미가 없는 assign이다
그 다음 이걸 바탕으로 다음단계를 수행한다
두 번째에서는 현재 assign된 클러스터들이 있는데
매 step마다 cluster들의 데이터포인트를 기준으로 모은 다음에
그 cluster들의 center를 정한다
이걸 centroid라고 한다
centroid는 cluster안에 들어가있는 데이터들의 평균이다
그럼 각각의 클러스터들의 센터점이 나오게되는데
k=5인 경우는 center도 5개가 나오게 되는 것이다
그럼 우리가 센터점을 구했으니 데이터포인트들을 바라보면서
각각의 cluster에 가까운 점들을 reassignment해주자
이렇게 reassignment를 하면 center가 바뀌게된다
그럼 또 새로운 center를 바탕으로 데이터포인트들을 reassign해주자
이걸 계속해서 반복하다가
센터점을 구한 다음 이전 iteration기준으로 데이터포인트들의 assign이 바뀌는게 없을 때 멈춘다

위에서는 k-means 알고리즘을 그냥 단순하게 몇 줄로 설명했는데
아까 k-means의 목적은 WCV를 줄이는 것이라고 했는데
위 알고리즘은 WCV의 최소점을 찾는다는 보장이 없다
그런데 아까 우리가 위에서 봤던 k-means의 objective를 잘 보자
우리가 k-means를 수행하면 step마다 위 식은 늘 작거나 같아진다
그런데 위 objective안의 식은 pair-wise 기준인데
우리가 수행한 k-means 알고리즘은 centroid 기준이라 다르지 않은가?
우리가 k-means의 식을
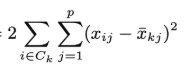
이렇게 위와 같이 정리할 수 있는데
이 식은 결국 위 objective 함수와 수학적으로 동일하다고한다

여기서 xbar는 한 클러스터의 centroid
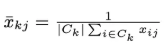
이렇게 나타낼 수 있는데 결국 식이 동일해진다고한다
아무튼 그래서 k-means는 사실상 오른쪽 식을 줄이는 알고리즘인데
결론적으로 왼쪽의 식도 줄어든다고 한다
그래서 k-means의 매 step을 수행할 때마다
증가하지 않는다는 것을 알겠다
그러면 식이 같아질 때는 언제인가?
그건 바로 이전 iteration이랑 데이터포인트들이 똑같았을 때
즉, k-means가 멈췄을 때이다
실제로 k-means가 계속 수행되는 동안에는 decrease한다
하지만 이 objective 함수가 감소한다는 보장은 있는데
그렇다고해서 minimum을 달성한다는 보장은 없다
그렇다면 이러한 이유는 뭘까?
우리가 이전에 배운 subset selection에서 stepwise도
반드시 best solution을 찾는다는 보장은 없었다
그 이유는 greedy search이기 때문이다
k-means도 마찬가지이다
k-means를 수행했을 때 global optimum을 찾지 못하는 것은
greedy하게 찾기 때문이다
어떤 학생이 질문에서 맨 처음에 random하게 cluster를 부여하는 것 때문은 아니냐고 질문했는데
이 random한 부여때문에 k-means를 수행할 때마다 결과가 달라질수는 있다고한다
그러나 그렇다고해서 그게 최적의 결과를 찾지못하는 이유는 아니라고한다

앞에서도 말했지만 true cluster는 없다
아무튼 우리는 위의 검은색 data로 k-means를 돌려볼 것이다
k=3으로 설정해줬다
첫 단계는 randomly cluster assign이기 때문에
각 데이터포인트를 random하게 assign해줬다
얘네들이 cluster assign이 되어있으니까 이제 centroid를 구해보자
그래서 세번째 iteration1, step2a에서 centroid를 구했고 이게 큰 동그라미이다
이렇게 새로 centroid가 구해졌으면 이를 기준으로 가까운애들을 reassign한다
그러고 재배정이 됐으니까 다시 센터점을 구한다
그런 다음 또 reassign을 하고 이 과정을 계속 반복하다가
어느순간 이전 Iteration이랑 달라지는게 없을 때 멈추게 된다
각 cluster들끼리 꼭 포함된 데이터포인트의 개수가 같지 않을 수는 있다
그리고 뒤에가서도 나오지만 데이터들을 반드시 standarization해줘야한다
clustering에서는 데이터의 범위가 매우 영향을 미치기 때문이다
그런데 clustering을 한다는 것이 결국 각각의 feature들의 중요도가 동일하다고 보는 것인데
사실 이 각각의 feature들이 동등하지 않을 수도 있다
그래서 우리가 이러한 것들을 decision을 해야한다
앞에서도 말했지만 clustering은 정답이없다
그래서 우리가 standarization을 수행해서
'나는 그냥 모든 feature들의 중요도가 동일하다고 가정할래!'라는 것도 나의 decision인 것이다
예를 들어서 학생들을 clustering하는데 성적, 학과, 지역 등 모든 feature들을
다 동등하게 바라보면서 clustering을 해야할까?
아니면 어떤 특정 feature를 더 중요하게 설정할까?
이런것들을 결정하는데에는 정답이 없는 것이다

위는 아까 똑같은 데이터를 k=3으로 여러번 돌렸을 때 나온 결과들이다
결과가 같게 나온 것도 있고 다르게 나온 것도 있다
앞에서도 말은 했지만 여기서 색은 그냥 clustering을 구분해주는것 외에는 아무 의미가 없다
두번째랑 세번째는 색은 다르지만 결국 동일한애이다
그러고 위의 숫자는 WCV의 summation 값이다
어떤건 더 높고 어떤건 더 낮다
당연히 낮을 수록 좋은거긴한데 앞에서도 말했지만
늘 global minimum으로 수렴하지 않기 때문에 한 번만 수행해서는
이 값이 가장 낮은값인지 아닌지 알 수가 없다
그렇다면 이렇게 같은 데이터에 대해서 동일하게 k=3으로 수행했는데
결과가 달라질 수 있는 이유는
가장 처음에 모든 데이터포인트들에 random하게 assign했기때문이다
그럼 이렇게 돌릴때마다 결과가 달라지는데 우린 어떻게 해야하나?
k-means를 수행할 때는 한 번만 수행해서는 안된다
적어도 여러 번 돌린다음 그 중에서 WCV summation이 가장 작은 것을 사용해야한다
물론 이것도 최소라는 보장은 없다

그 다음으로는 hierarchical clustering을 살펴보자
이건 k와 같은 하이퍼파라미터를 설정하지 않아도 된다
위 방법은 bottom up과 top down 두 가지 방법으로 모두 할 수 있는데
이번 설명에서는 bottom up으로 설명한다
보통 이 hierarchical clustering을 수행할 때는 bottom up으로 하고
이를 어려운말로는 agglomerative라고 한다
이런 예시가 있다고 해보자
feature가 2차원인 데이터포인트들이고
clustering이 그냥 이렇게 됐다고 해보자

위 결과를 가지고 hierarchical clustering을 한 결과이다
아까도 말했지만 매 단위마다 clustering에서의 merge가 발생한다
얘네들이 그래서 하나로 다 뭉쳐질때까지 수행한다
그런 다음에 사후적으로 clustering을 수행하는 것이다
어느 시점에서 자를지를 내가 얘기할 수 있다
위 예시에서 결과를 보니 클러스터를 3개 정도로 나누는게 적절할 것 같다라고하면
가장 오른쪽의 저 점선에서 자르면 되는 것이다
그럼 총 3개의 가지가 남게되는데 이들이 서로 클러스터가 되는 것이다
그리고 위 tree에서 높이차이는 merge할 때 발생하는 reduction이다
잘랐을 때 reduction이 얼마나 있었는지를 바라보는 정도이고
길이가 길수록 데이터들이 충분히 떨어져있다는 뜻이다
그래서 길게 길게 자르는 것이 적절히 떨어져있구나~ 생각하며 통상적으로 좋다고 한다
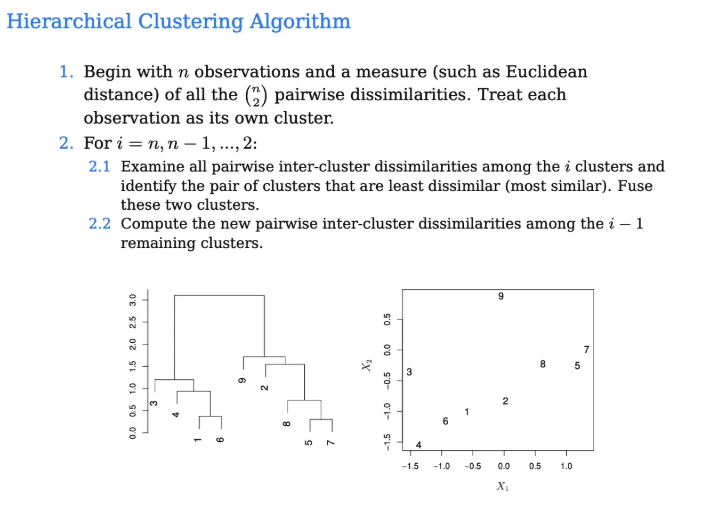
hierarchical clustering은 매 step마다 클러스터들끼리 merge를 수행하는 것이다
첫 단계에서는 각각의 데이터포인트들이 자기 자신의 클러스터가 된다
주의해야할 점은 데이터포인트들을 merge하는 것이 아니다
클러스터들끼리 merge하는 것인데
최초에는 각각의 데이터포인트들이 하나의 cluster가 되므로 이를 merge하는 것이다
따라서 데이터포인트가 n개가 있다면 처음의 클러스터도 n개가 된다
그래서 이 클러스터별로 pair-wise로 살펴보는데
이 각각의 데이터포인트(클러스터)중에서 유클리드거리 기준으로 가장 가까운건 5랑 7이 될 것이다
따라서 이걸 그럼 첫 번째로 묶어버리자
그럼 이제 5와 7은 한 덩어리가 되어서 절대 떨어지지않는 1개의 cluster가 된다
이제 다음 step으로 넘어가보자
그 다음에는 1과 6이 가장 가까워보인다
이것도 데이터포인트끼리 묶는게 아니고 각 클러스터기때문에 merge하는 것이다
그래서 1과 6도 묶어주었다
그렇다면 1과6이 묶였고 5와 7이 묶이게 되었다
그 다음에는 8과 (5,7)이 가까워보인다
그렇다면 이것도 묶어준다
그래서 이렇게 계속해서 묶어주면서 이게 한 개의 덩어리가 될 때까지 반복해준다

위에서 설명한 내용을 시각화하면 위와 같다

데이터포인트들끼리의 거리만 구할 때는 그냥 유클리드 거리만 구하면 됐는데
만약 클러스터들끼리 거리를 구한다고 한다면 어떻게 거리를 계산해야할까?
클러스터 안에 데이터포인트들이 여러 개가 있기 때문이다
이걸 linkage라고 부르는데 총 3가지가 존재한다
첫 번째 simple linkage는 클러스터가 2개가 있으면
그 중에서 가장 가까운 애들끼리 minimum distance를 기준으로 삼는 것이다
complete linkage는 2개의 클러스터 중에서 가장 먼 애들로 거리 기준을 잡는 것이다
가장 먼 애들끼리 바라봤을 때 그 거리가 가장 작다면 merge되는 것이다
마지막 average linkage는 각각의 데이터포인트들의 평균을 기준으로 한다

실제로 똑같은 데이터인데 linkage를 뭘로 하냐에 따라서 클러스터의 순서도 결과도 달라진다
그리고 또 클러스터간의 거리도 항상 유클리드로 하지 않아도 된다
이것도 결국 우리가 다 결정하는 것이다

그렇다면 .. 늘 나오는 질문인
우리는 뭘 사용해야될까?
정답은 없다
우리의 apporach가 무엇이냐에 따라서 결정하면 되는 것이다
k-means건 hierarchical이건 클러스터링에서 중요한 것은
각각의 variable의 scale에 depend한다
distance를 기준으로 하기 때문이다
그래서 꼭 standarize를 해주는게 좋다
하지만 아까도 말했지만 클러스터링을 해서 각각의 feature를 동등하게 바라보는 것도
결국 철학적으로 내가 결정을 내리는 것이다
hierarchical clustering을 수행해서 k를 뭘로할지 결정한 다음
k-means로 가져가서 수행하는 경우도 있다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Deep Neural Networks (0) | 2025.11.02 |
|---|---|
| [DL] Shallow Neural Network (0) | 2025.10.29 |
| [ML] Principle Components Analysis (PCA) (0) | 2025.10.17 |
| [ML] Support Vector Machine (SVM) (0) | 2025.10.15 |
| [ML] Tree-based Methods 2편 (Bagging, Random Forests, Boosting) (0) | 2025.10.13 |