본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간에 배울 내용은 Principle Components Analysis
우리나라말로는 주성분분석이다

우선 unsupervised learning에 대해서 배워보자
오늘 배울 PCA는 대표적인 unsupervised learning 중에 하나다
unsupervised learning은 우리 수업 1강에 잠깐 나왔는데
x와 y의 관계를 학습하는 것이 우리가 지금까지 배운 supervised learning이라면
unsupervised learning은 y값이 아닌 feature들에만 관심이 있다
y값이 아예 없을 수도 있고, 혹은 있지만 아예 관심이 없다
그래서 PCA는 예를 들어서 100차원의 feature가 있다고 한다면
이걸 projection을 통해서 어떻게하면 데이터의 손실을 최소화화며
Feature의 차원을 줄일까하는 문제이다

아무튼 unsupervised learning의 대표적인 예시에 대해 한 번 살펴보자
clustering이 대표적인 예시 중 하나인데
예를 들어 100명의 수강생을 5개의 그룹으로 나누고 싶은데
갖고 있는 정보가 학과, 성별, 전공 등이 있다
이런 정보들을 활용해서 수강생을 어떻게 5개의 그룹으로 나눌지는
정답이 없는 문제이다
이러한 정답이 없는 문제를 해결하는 것들이 비지도 학습이다
이번 시간에 다룰 PCA는 위에서도 말했지만 차원축소를 수행하는 것이다
data visualization을 위해서 2차원으로 많이 변경하곤하지만
반드시 이것만을 위해 사용되는 것은 아니다
PCA는 아주 general한 방식이고
supervised learning을 하기 전에 데이터 preprocess 단계로도 많이 사용된다

이런 unsupervised learning은 정답이 없는 문제이기떄문에
주관적일 수밖에ㅐ 없다
supervised learning처럼 정답을 바탕으로
이건 잘했어! 이건 못했어!를 가늠할 수가 없는 것이다
그래서 아주 넓게 생각하면 가지고 있는 데이터를 가지고
정답이 없는 것을 수행하는 것이 바로 비지도학습이다
앞에서 배운 supervised learning은 사실 굉장히 편한 케이스이다
왜냐하면 정답도 이미 있고 내가 거기에 맞춰서 prediction만 하면 되는 것이기 때문이다
하지만 현실의 데이터는 그렇지 않은 경우가 많다
특히 요즘같은 빅데이터 시대에는 unlabel 데이터가 굉장히 많기 때문에
그 unlabel 데이터를 분석해서 underlying을 학습하는
unsupervised learning이 많이 중요해졌다

PCA에 대해서 이제 본격적으로 살펴보자
PCA는 x 변수들만 살펴본다
그 x 변수들을 low dimension으로 representation 할 수 있을까 하는 것이다
PCA에서는 이를 위해서 우선 분산이 큰 쪽을 찾는다
분산이 크다는 것은 데이터가 그쪽 방향으로 많이 퍼져있다는 뜻이다
사실 처음에는 이게 잘 이해가 안되어서 gpt에게 물어봤다
그랬더니 정보이론에서는 분산이 크다 = 데이터의 다양한 패턴을 볼 수 있다 = 데이터의 정보가 많다
로 정리될 수 있다고 한다
그럼 한 가지 생각이 들 수 있다?
심각한 이상치 1개 때문에 그쪽이 분산이 너무 커지면
그 방향도 정보가 많다고 보냐?
계산적으로는 그렇게 될 수 있기 때문에
PCA에서는 다른 방법보다 정규화와 noise 제거가 중요하다고 한다
아무튼 PCA는 우선적으로 데이터에서 분산이 가장 큰 방향을 찾는다
위 ppt 예시에서는 눈으로 봤을 때 왼쪽 대각선으로 올라가는 방향이 될 것이다
이 방향이 그럼 PCA의 첫 번째 축이 되는 것이다
이 축이 linear algebra에서 말하는 basis이다
따라서 이 축에 데이터들을 다 projection을 수행하면
원래 2차원이었던 데이터들이 1차원으로 나타낼 수 있게 된다
지금 예시는 2차원을 1차원으로 변환하는 것이지만
100차원을 2차원으로 변환하는 것도
위의 과정을 계속해서 반복해서 2차원까지 수행하는 것이다
앞에서도 말했지만 이걸 수행하는 이유는
데이터 시각화를 위해서일수도 있고
supervised learning을 수행하기 전단계일수도 있다
그리고 위 예시에서 y축에 있다고 다 y값이 아니다
x1, x2라는 feature들의 값이다

PCA에서 가장 중요한 것은 처음의 first principle component이다
우리가 만약에 feature가 p개가 있다고 하면
X1, X2, ... , Xp까지 feature가 있다
그럼 이걸 바탕으로 linear combination을 해서 어떤 새로운 벡터값인
Z1을 만들 수 있다
각 feature과 각각의 가중치, 여기서는 loading이라고 부르는데
이 loading들의 값을 결합해서 새로운 어떤 축, 벡터를 만들 것이고
이 새롭게 만들어지는 벡터는 분산이 가장 커야한다
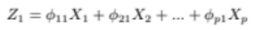
위 loading들을 다르게 하면 이 벡터의 방향이 달라지기 때문에
우리의 목표는 이 loading들을 최대한 잘 조절해서
벡터의 방향이 분산이 가장 큰 방향과 같아지게 하는 것이다
그런데 이 loading 값에 아무런 제약이 없으면
loading이 계속해서 커지면 커질수록 분산은 계속 커지게된다
하지만 이건 진짜로 분산이 큰 방향을 찾는 것이 아닌
그냥 단순히 스케일만 커지게 한 것일 뿐이다
따라서 우리는 이 loading 값들에 constraint를 줘서
길이는 고정시킨 다음 그 방향만 조절할 수 있게 한다

이렇게 각 loading들의 제곱의 합이 1이 되도록 조절한다
이런 constraint는 앞의 SVM에서도 봤었는데
이 말인 즉 radius가 1인 어떤 구안에 벡터가 존재하는 것이고
그 구 안에서 계속해서 방향만 바꿔간다고 생각하면 된다
이렇게 방향을 바꿔가면서 linear combination의 variance가 가장 큰 방향을 찾는 것이다
총 feature의 개수는 p개이고 첫 번째 principle component에 대한
loading값이기 때문에 뒤에 1이 붙는다

총 데이터포인트는 n개, feature의 수는 p개가 있어서
데이터 X의 차원은 n x p이다
PCA를 할 때는 이 데이터들의 평균을 0으로 맞춰주는 (mean-zero)
정규화 과정을 반드시 거쳐야 하는데
우리는 이 데이터들의 분산에만 관심있기 때문이다
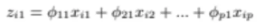
위 식에서 xi1, xi2, ..., xip들은
i번째 데이터포인트의 1번부터 p번째 feature들의 값이고
위 식으로 계산하면 i번째 데이터포인트들이 새로운 데이터포인트 zi1이 나오게 된다
우린 이 z값을 score라고 부르는데
위 과정을 전체 데이터포인트에 대해서 다 수행해주면
score는 총 데이터포인터의 개수인 n개만큼 나오게 된다
z11, z21, z31, ..., zn1까지 나오게 되는 것이다
그럼 우리가 각 데이터포인트에 대해서 새로운 데이터포인트를 각각 구했는데
저 새로운 데이터포인트들, score값들이
각 데이터포인트들에서 어떤 새로운 축에 projection된 값들이다
따라서 이 projection된 값들의 분산이 가장 큰 것이
우리가 찾고자하는 first principle component가 될 것이다
따라서 각 값들의 분산을 구해서 이걸 젤 크게 하면 되는데
아까 우리가 데이터포인트들을 mean-zero로 맞추었기 때문에
score값들의 평균도 0이 된다
그렇기 때문에 score 값들의 분산을 계산하기 간편해지는 것이다



gpt가 해준 설명이 이해하기 쉬운 것 같아서 추가했다

그럼 위에서 우리가 하고싶었던게 score들의 variance를 최대화하고 싶었던 것이다
그럼 한 번 해보자
평균이 0이기 때문에 각 score들의 제곱의 합에
데이터포인트들의 개수인 n만 나눠주면 된다

따라서 위 식처럼 되는데 이걸 다시 쓰면
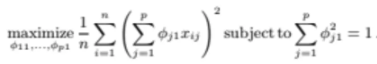
위 식이 된다
그냥 score를 우리가 아까 적었던 linear combination식으로 넣어준 것이다
결국 이걸 maximize하는 loading들을 찾겠다는 말이다
사실 이건 linear algebra에서 나오는 singular-value decomposition으로 쉽게 구할 수 있다
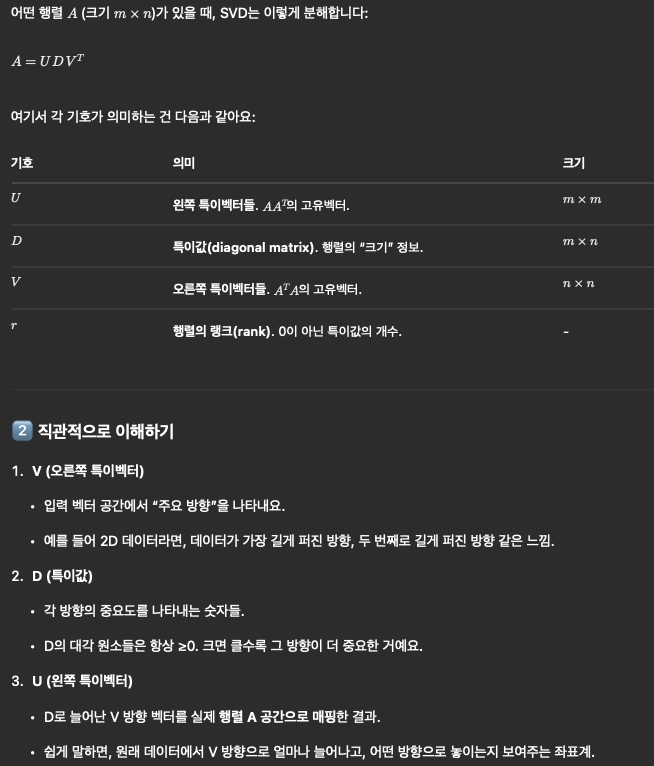
선형대수 강의를 4년전에 들어서 SVD가 잘 기억이 안나서
gpt한테 살짝 물어봤다 ㅎ..
관련해서 강의를 한 번 찾아봐야할 것 같다
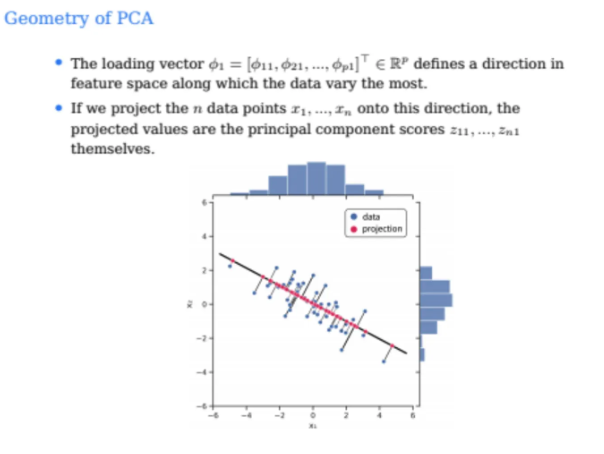
우리가 위처럼 구한 로딩벡터는 결국 feature space에서
데이터가 어느 방향으로 가장 많이 움직이는지를 가리킨다
위 데이터에서는 오른쪽 아래 방향이 basis의 방향이 된다고 한다
그래서 위에서 basis를 구해서 원본 데이터에서 Projection을 수행한 것이
빨간색 점들로 나타나져있다
그럼 이 projection된 점들은 각 데이터포인트들의 score값이 되는 것이다

지금까지 우리가 살펴본건 first principle component만 관한 얘기였다
하지만 우리는 실제 PCA에서 이걸 한 번만 할 수 없다
예를 들어서 100 dimension의 feature를 2 dimension으로 한다고 해보자
첫 번쨰 first principle component는 찾았다고 치자
그럼 second principle component는 어떻게 찾을까?
second principle component는 first principle component와
uncorrelated 되어있어야 한다
그게 무슨 뜻이냐?
쉽게 생각해서 first principle component에서 가장 분산이 큰 축을 찾았으니
그 다음으로 분산이 큰 축을 찾으면 된다고 생각할 수 있겠지만 그렇지 않다
두번쨰로 분산이 큰 축은 우리가 이전에 처리한 가장 분산이 큰 축과 거의 유사할 수밖에 없다
그렇게 한다면 거의 똑같은 정보를 두번이나 설명한셈이 되는 것이다

따라서 second principle component는 그렇게 하지않고
첫번째에서 uncorrelated된 축을 찾는다
그게 한 마디로 orthogonal(직교)한 축이 되는 것이다
따라서 first principle component와 수직인 방향인 축들 중에서
또 가장 variance가 큰 축을 찾으면 되는 것이다
우리가 앞에서 본 예시는 2차원이었기 때문에
직교하는 방향이 1개밖에 없는 것이지만
100차원이라고 한다면 직교하는 방향은 99개가 나오게 된다
p dimension이라고 한다면 first principle component를 찾아내면
p-1차원이 남게 되는 것이다
그럼 이 중에서 직교하는 p-1개의 방향 중에서 가장 variance가 큰 것을 찾으면 된다
이걸 계산하는 방법도 앞과 동일하다
결국 loading vector들을 찾는 문제이고
square summation이 1인 loading vector들로
첫번째와 직교하는 방향 중 가장 variance가 큰 loading 벡터를 찾는 것이
second principle component를 찾는 문제이다
그럼 세번째 principle component는 어떻게 찾을까?
첫번쨰랑 두번째를 찾았기 때문에
첫번쨰와 두번째와 직교하는 방향 중에서 variance가 가장 큰 방향을 또 찾으면 된다
그럼 이 PCA 문제를 계속해서 이렇게 순차적으로 풀 수 있을까?
아까도 말했지면 singular-value decomposition으로 하면
한 번에 구할 수가 있다고 한다

위 gpt의 설명을 참고하면 좋을 것 같다
그럼 마지막으로 우리는 이러한 주성분을 몇개까지 찾을 수 있을까?
min(n-1, p)라고 하는데 p는 변수의 차원이니까
우리가 x의 차원보다 더 작게 주성분을 찾을 수는 없으니 이해할 수 있다
그런데 n-1은 뭘까?
왜 n이 아니고 n-1이 되는걸까?
우리가 아까 앞에서 mean-zero로 모든 데이터들을 정규화시켜줬다
우리가 이 작업을 수행하는 순간
모든 데이터포인트들의 평균은 0이 되어야한다는 constraint가 생기게 된다
이 제약조건때문에 우리는 자유도를 하나 잃는 것이다

위 예시를 생각하면 이해가 편할 것 같다

미국의 50개의 주에 대해서 4개의 범죄 데이터를 바탕으로
PCA를 수행해본 결과이다
이 데이터포인트는 50 * 4인 데이터이다
위 그림에서 x축은 각 데이터포인트별 first principle component의 값이고
y축은 second principle component의 값이다
즉, zi1, zi2 값들이라는 것이다
그리고 주황색 vector들은 각 feature들의 loading vector값
즉, 각 feature들이 PC1, PC2에 얼마나 영향을 미쳤는지를 나타내는
가중치 값이 된다
따라서 urban pop(=도시 인구)의 경우 오른쪽 위로 갈수록
인구가 많아지는 것이고 왼쪽 아래로 갈수록 인구가 적어지는 것이다
다른 범죄들도 마찬가지
대체적으로 오른쪽으로 향할수록 범죄가 증가하는 경향이 있다
그 말은 왼쪽에 있는 state들은 범죄가 상대적으로 적다는 뜻이다
얘네들이 어떻게 PCA가 된 것인지 한 번 정리해보자
4개의 범죄 feature를 다운 4차원의 데이터를
2차원으로 축소한 것이다
그런데 만약 내가 축소를 한 번 더해서 1차원으로 만들고싶다?
그러면 그렇게 해도 된다
위 예시는 2개의 차원을 축소했기 때문에
variance가 가장 큰 2개의 방향을 찾았고
그 방향으로 proejction을 수행해서 차원을 축소한 것이다
그런데 이렇게 하면 당연히 정보의 손실이 생긴다
따라서 이 정보의 손실을 가장 적은 쪽으로 하기 위해
variance가 큰 방향으로 projection을 하는 것이다

gpt의 설명을 참고하면 좋을 것 같다

위 그림은 original data는 4차원인데 2차원으로 나타낸 것이라고 한다

그렇다면 linear regression과 PCA를 살짝 비교해보자
결국 둘다 어떠한 데이터포인트들을 기준으로
최적의 선을 찾는다는 점에서는 동일하다
하지만 linear regression에서는 단순히 수직 방향만으로
line과 데이터포인트들의 차이를 구한다
오직 y값만을 기준으로 오차를 구하고 그게 RSS가 된다
이건 Projection이 아니다
하지만 PCA는 단순 수직 방향이 아닌
모든 방향에서 loading vector를 projection해서 가장 가까운 곳을 찾는 것이다

이번에는 scaling에 대해서 배워보자
위에서 살짝 언급했는데 PCA에서는 scaling은 특히 더 중요하다
물론 다른 방법을 사용할떄도 중요하지만
PCA와 clustering에서는 더더욱 중요하다
만약에 데이터에서 어떤 column은 0에서 1000 사이의 값인데
어떤 column은 단위가 작아서 0.1에서 0.2 사이의 값이 나온다고 하자
그럼 굉장히 sensitive한 결과가 나오게 된다
우리는 분산이 큰 방향을 찾아야 하는데 단위때문에
이에 혼동이 올 수 있다
우리가 아까 위에서 봤던 미국의 범죄 데이터 예시만 봐도
인구는 숫자 단위가 굉장히 클텐데 범죄는 그렇지 못하기 때문에
단위가 달라서 혼란스러워질 확률이 높다
따라서 scaling을 해주면 좋다
보통 scaling은 centering을 통해 mean zero를 만든 다음
표준편차가 1이 되도록 조정하는 standardization을 사용한다
linear regression 같은 경우는 scaling을 해도되고 안해도 되는데
lasso나 ridge같은 경우는 반드시 수행해야한다
그래서 그냥 애초에 scale을 해주는게 마음이 편할 수도 있다

그럼 우리가 각각의 PC들을 구할텐데
이 PC들이 전체 분산에서 얼만큼을 차지하고있는지를 알아보자
그걸 나타내는 지표를 propotion of variance explained(PVE)라고 한다
우리가 데이터를 알고있으면 각 feature별 분산은 모두 구할 수 있다

위 식은 그냥 각 feature별 분산을 다 더한 값이다
그게 평균이 0이기 때문에 오른쪽으로 다시 정리할 수 있다
그리고 각각 m번째 score의 분산은

식으로 이렇게 표현할 수 있다
위 Zm의 분산은 우리가 결국 PC의 로딩벡터들을 구하기 위해
maximize했던 값이다
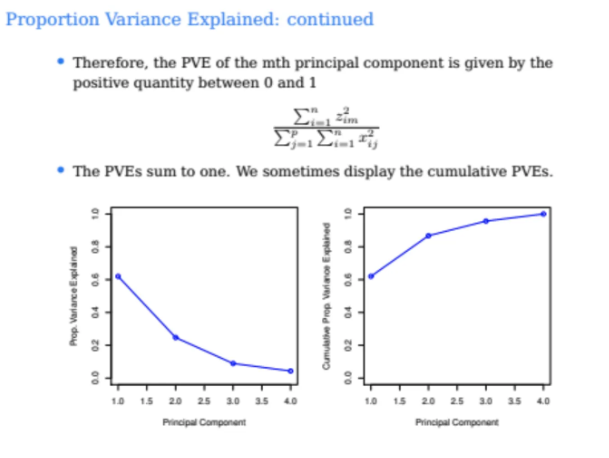
따라서 PVE는 아래와 같은 식으로 구할 수 있다

이게 결국 전체 데이터포인트들의 분산에서
m번째 pa의 분산의 비율이다
이 값은 그래서 0과 1 사이의 값으로 나오게 된다
모든 PC에서의 PVE를 다 더하면 1의 값이 나온다
따라서 위 ppt의 그래프는 cumulative PVE를 구한 것이다
PC1의 PVE는 60%가 나온 것을 확인할 수 있다
그 다음은 0.8을 조금 넘으니 PC2는 20% 정도를 차기하고 있음을 알 수 있다
PVE는 첫번째, 두번쨰, 세번째 이렇게 쭉쭉 갈수록
monotone하게 decrease 할 수 밖에 없다
왜냐하면 우리가 첫번째 PC는 가장 분산이 큰 방향으로 해주었고
두 번째 PC는 첫번쨰를 제외하고 그 다음으로 분산이 큰 방향으로 해준 것이기 때문이다
따라서 계속 뒤로 갈수록 점점 줄어들 수밖에 없는 구조를 갖게된다

gpt의 설명을 참고하면 좋을 것 같다
그럼 여기서 질문이 있다
우리는 PCA를 수행할 때 몇개의 PC를 구하는게 가장 효율적일까?
사실 정답은 없는 문제이다
우리가 위 예시만 봐도 100개의 차원이 있었는데
그 중에서 4개만 PC를 구해도 거의 99% 가까이를 설명할 수 있었다
그럼 이 데이터들이 상당히 서로 correlated 되어있어서
100차원이지만 4개의 차원으로도 충분히 설명이 가능하다는 뜻이된다
PVE를 구하다보면 전체 차원에 대해서 다 PC를 구하면
당연히 100%로 본 데이터를 설명할 수 있다
뒤로가면 데이터 전체를 다 설명한다고 무조건 PC를 많이 찾으면?
사실 그럼 차원축소를 하지 않고 그냥 원본 데이터를 쓰는 것과 똑같다..
아무튼 주어진 데이터에서 정해진 PC 개수라는 것은 없지만
아까 위에서 언급한 singular-value decomposition으로 구할 수 있긴 하다
여기서 구해진 singular value들은 singular들이 큰 값 순서대로 정렬이 된다
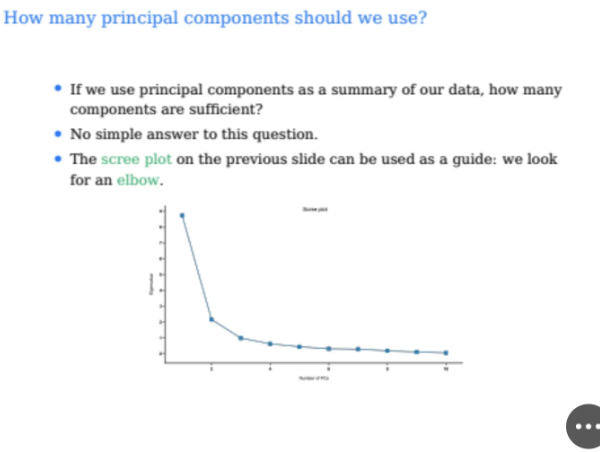
따라서 이 값들을 시각화해서 그래프를 그리다보면
매우 가파르다가 어느 순간부터 확 꺾이는 변곡점이 보일 수가 있는데
이를 elbow라고 부른다고 한다
아무튼 그래서 이 확 꺾이는 지점부터는
PC의 영향력이 작다는 뜻이 되므로
해당 지점까지만 하면 되겠다고 생각할 수 있지만
100% 신뢰할 수는 없다고 한다
왜냐하면 singular-value decomposition을 해도 elbow가 없는 경우도 있고
elbow가 여러개인 지점도 있을 수 있기 때문이다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Shallow Neural Network (0) | 2025.10.29 |
|---|---|
| [ML] Clustering (k-means clustering, hierarchical clustering) (0) | 2025.10.27 |
| [ML] Support Vector Machine (SVM) (0) | 2025.10.15 |
| [ML] Tree-based Methods 2편 (Bagging, Random Forests, Boosting) (0) | 2025.10.13 |
| [ML] Tree-based Methods 1편 (Decision Trees) (1) | 2025.10.12 |