이번엔 수업시간에 배운
MaxHeapify를 바탕으로
HeapSort를 구현해보려고 한다
MaxHeapify와 HeapSort의 내용은 아래에 있다
https://think0905.tistory.com/entry/computer-science-Binary-Tree-Max-Heap
[computer science] Binary Tree, Max Heap
이 게시글은서울대학교 데이터사이언스대학원조요한 교수님의데이터사이언스 응용을 위한 컴퓨팅 강의를학습을 위해 재구성하였습니다.중간고사가 지나고 이전까지는 기본적인c++에 대해서
think0905.tistory.com
https://think0905.tistory.com/entry/computer-science-Heap-Sort%EC%99%80-Priority-Queue
[computer science] Heap Sort와 Priority Queue
이 게시글은서울대학교 데이터사이언스대학원조요한 교수님의데이터사이언스 응용을 위한 컴퓨팅 강의를학습을 위해 재구성하였습니다.이전 시간에 이어 이번에는Heap Sort와 Prioirity Queue 내용
think0905.tistory.com
HearSort 알고리즘의 순서는 다음과 같다
1. maxHeap의 형태로 만들어주는 maxHeapify 구현
2. 그냥 array를 maxHeap으로 만드는 buildMaxHeap 구현
3. buildMaxHeap을 하고 sort를 진행하는 HeapSort 구현
하나씩 차근차근 살펴보도록하자
maxHeapify
array와 array.size()인 n, index인 i를 input으로 받는
maxHeapify를 구현해보자
이는 array에서 해당 index로 찾아가
값을 비교하며 maxHeap의 구조를 만족하게끔
fix-up해주는 알고리즘이다
maxHeap의 구조에서 i번째 노드의 left와 right의
index는 각각
left = 2i + 1
right = 2i + 2
이다
따라서 parent node인 i번째 index의 값과
left와 right를 비교해서
i번째 값이 더 작으면 maxHeap의 구조를
만족시키지 않고 있으므로
값을 교환해준다
그렇게 recursive하게 leaf node로 갈 때까지
해당 과정을 반복해준다
이는 maxHeap의 height만큼 순환하므로
time complexity는 O(log n)이다
maxHeapify의 코드는 아래와 같다
void maxHeapify(vector<int>& arr, int n, int i) {
// 자기 자신과 left, right node의 index 할당
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// left가 존재하고 left node가 parent인 n보다 크다면 largest를 left로
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// right가 존재하고 right node가 parent인 n보다 크다면 largest를 right로
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// largets가 i가 아니라면(left나 right 둘 중 하나라면) 둘을 교환하고 recursive
if (largest != i) {
swap(arr[i], arr[largest]);
maxHeapify(arr, n, largest);
}
}
buildMaxHeap
이제 위 maxHeapify 코드를 사용해서
그냥 array를 maxHeap의 구조로 바꾸는
buildMaxHeap 함수를 구현해보자
buildMaxHeap은 자식이 있는 node부터 시작해서
root node까지 차례로 올라오며
maxHeapify를 시켜줘야한다
따라서 전체 array의 size인 n에서
n/2-1부터 시작해서 하나씩 감소시키며
for loop를 돌려준다
buildMaxHeap의 코드는 아래와 같다
void buildMaxHeap(vector<int>& arr, int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
maxHeapify(arr, n, i);
}
}
heapSort
heapSort의 기본 순서는 다음과 같다
1. array를 maxHeap으로 만든다 (buildMaxHeap)
2. 가장 큰 root node를 맨 뒤로 보낸 뒤 제외 -> 새로운 root에 대해 maxHeapify
3. array의 element에 대해서 2번 반복
코드는 아래와 같다
void heapSort(vector<int>& arr) {
int n = arr.size();
// array를 maxHeap으로 바꾸기
buildMaxHeap(arr, n);
// array에 대해서 root를 마지막으로 보내고 제외 -> 새 root에 대해 maxHeapify
for (int i = n-1; i>=0; i--) {
swap(arr[0], arr[i]);
maxHeapify(arr, i, 0);
}
}
이제 main함수에서 HeapSort가 잘 되는지
한 번 실행해보자
main 함수는 아래와 같이 구현해봤다
int main () {
vector<int> arr = {12, 11, 13, 5, 6, 7};
cout << "정렬 전 배열: ";
for (int num : arr)
cout << num << " ";
cout << endl;
heapSort(arr);
cout << "정렬 후 배열: ";
for (int num : arr)
cout << num << " ";
cout << endl;
return 0;
}
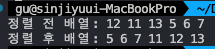
위와같이 heapSort의 결과가
정상적으로 잘 sorting된 것을 확인할 수 있다
전체 코드는 아래와 같다
#include <vector>
#include <queue>
#include <iostream>
#include <algorithm>
using namespace std;
void maxHeapify(vector<int>& arr, int n, int i) {
// 자기 자신과 left, right node의 index 할당
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// left node가 parent인 n보다 크다면 largest를 left로
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// right node가 parent인 n보다 크다면 largest를 right로
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// largets가 i가 아니라면(left나 right 둘 중 하나라면) 둘을 교환하고 recursive
if (largest != i) {
swap(arr[i], arr[largest]);
maxHeapify(arr, n, largest);
}
}
void buildMaxHeap(vector<int>& arr, int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
maxHeapify(arr, n, i);
}
}
void heapSort(vector<int>& arr) {
int n = arr.size();
// array를 maxHeap으로 바꾸기
buildMaxHeap(arr, n);
// array에 대해서 root를 마지막으로 보내고 제외 -> 새 root에 대해 maxHeapify
for (int i = n-1; i>=0; i--) {
swap(arr[0], arr[i]);
maxHeapify(arr, i, 0);
}
}
int main () {
vector<int> arr = {12, 11, 13, 5, 6, 7};
cout << "정렬 전 배열: ";
for (int num : arr)
cout << num << " ";
cout << endl;
heapSort(arr);
cout << "정렬 후 배열: ";
for (int num : arr)
cout << num << " ";
cout << endl;
return 0;
}
'기술 > 알고리즘' 카테고리의 다른 글
| [c++] BFS/DFS 구현하기 (넓이우선탐색, 깊이우선탐색) (0) | 2024.12.16 |
|---|---|
| [c++] Min Cost to Connect All Points 문제 Prim's Algorithm으로 해결하기 (1) | 2024.12.13 |
| [c++] Find the Hub 문제 Floyd-Warshall Algorithm & Bellman-Ford Algorithm으로 해결 (1) | 2024.12.06 |
| [c++] Height Order 문제 해결하기 (Floyd-Warshall's Algorithm, Topological Sort) (2) | 2024.12.05 |
| [c++] tree structure를 base로 한 max heap 구현하기 (1) | 2024.12.02 |