이번 수업시간에서 MST(Minimum Spanning Tree)에 대해 배워
관련 알고리즘 문제들을 LeetCode에서 찾아 풀다가
MST에서 간단한 문제를 정리해보기로했다
[computer science] Graph, Tree, Minimum Spanning Tree(Prim's, Kruskal's Algorithm)
이 게시글은서울대학교 데이터사이언스대학원조요한 교수님의데이터사이언스 응용을 위한 컴퓨팅 강의를학습을 위해 재구성하였습니다.이번 시간에는 graph와 tree에 대한기본 용어 및 개념 복
think0905.tistory.com
Minumum Spanning Tree에 대한 설명은
위 링크에..!

코딩 문제의 설명은 위와 같다
각각 2d-plane형태의 좌표점들이 있고
이 좌표들간의 거리는
manhattan distance(|xi - xj| + |yi - yj|)로 계산한다
예시는 아래와 같다
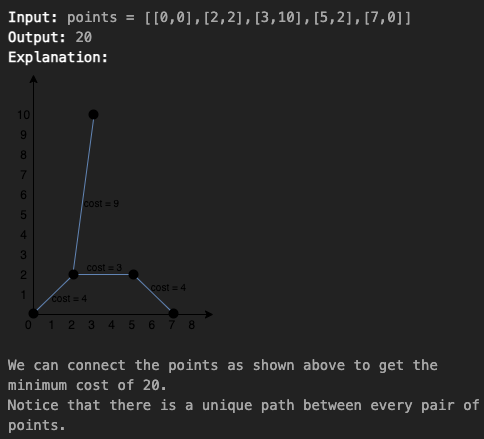
모든 좌표를 연결하는데
총 거리가 가장 짧을 때를
output으로 return하는 문제였다
constraints는 아래와 같다

모든 좌표를 연결하는데 총 거리가 가장 짧을 때니
무조건 MST 문제라고 생각했다
MST를 찾는 알고리즘은
1. Prim's Algorithm
2. Kruskal's Algorithm
2가지가 있는데
두 알고리즘에 대해 간단히 요약하자면
Prim's는 edge를 순차적으로 탐색해나가는 방식이고
Kruskal's은 전체 edge를 한 번에 비교하는 방식이다
위와 같은 문제의 경우는
좌표와 좌표 사이가 모두 edge가 되므로
Kruskal's은 좀 부담이 클 수 있겠다고 생각했다
그래서 Prim's를 이용해서 해결하기로 했다
Prim's Algorithm의 순서는 아래와 같다
1. cycle 확인을 위한 visited vector 선언
2. 가장 cost가 낮은 edge를 찾기 위한 minimum priority_queue 선언
3. priority_queue에 대해서 while문 돌면서
이웃한 edge들 탐색 + distance 계산
위의 순서대로 차근차근 코드를 구현해보자
visited Vector와 minimum_prioirty_queue 구현
우선 나같은 경우는 priority_queue를 정의할 때
가중치와 노드번호를 담을 pair를 정의해줬는데
pair<int, int>로 계속 쓰기 귀찮아서
typedef로 미리 정의를 해줬다
typedef pair<int, int> Edge; // 가중치, 노드번호
그런 다음 cycle확인을 위해
각 node 번호마다 방문 여부를 true, false로 저장해줄
visited vector를 선언해주고
아래에 minimum_priority_queue를 선언해준다
vector<bool> visited(points.size(), false);
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
priority_queue에 대해서 while문 돌면서 이웃한 edge들 탐색 및 distance 계산
우선 총 경로를 저장해줄 distance 변수를 선언해준다
그러고 minimum priority queue에
가장 첫번째 node를 0번째 index로 push해준다
그리고 queue를 while문 돌면서
현재 queue 중 가장 weight가 낮은 edge를 선택해서
visited가 true인지 확인해준다
visited가 false면 distance에 weight를 더하고
visited를 true로 변경해준다
그러고 다시 이웃한 edge들에 대해서
manhattan distance를 계산한다음
queue에 push해준다
코드는 아래와 같다
int distance = 0;
// 0번째 node를 우선적으로 queue에 push
pq.push({0, 0});
// queue가 empty일 때 까지 while문 돌기
while (!pq.empty()) {
// 가장 edge가 낮은 node 꺼내기
auto [currWeight, currNode] = pq.top();
pq.pop();
// 해당 node가 이미 방문한 node면 과정 생략
if (visited[currNode]) { continue; }
// 현재 node에 대해서 weight를 더해주고 visited를 true로 해주기
distance += currWeight;
visited[currNode] = true;
// 현재 node에 대해서 전체 edge와의 manhattan distance 계산해서 queue에 push
for (int i=0; i<=points.size()-1; i++) {
if (!visited[i]) {
int dis = abs(points[currNode][0] - points[i][0]) + abs(points[currNode][1] - points[i][1]);
pq.push({dis, i});
}
}
}
전체 코드는 아래와 같다
#include <climits>
#include <cmath>
#include <queue>
typedef pair<int, int> Edge;
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
vector<bool> visited(points.size(), false);
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
int distance = 0;
pq.push({0, 0});
while (!pq.empty()) {
auto [currWeight, currNode] = pq.top();
pq.pop();
if (visited[currNode]) { continue; }
distance += currWeight;
visited[currNode] = true;
for (int i=0; i<=points.size()-1; i++) {
if (!visited[i]) {
int dis = abs(points[currNode][0] - points[i][0]) + abs(points[currNode][1] - points[i][1]);
pq.push({dis, i});
}
}
}
return distance;
}
};
모든 test case에 대해서 통과가 되었다

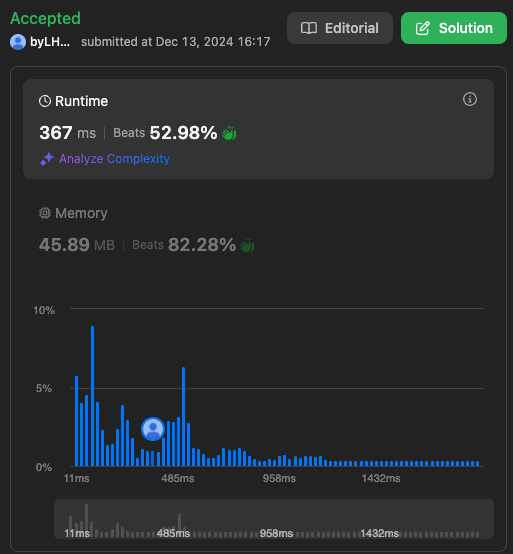
time complexity나 space complexity도
그냥 그럭저럭 적당했던 것 같다 ㅋ
'기술 > 알고리즘' 카테고리의 다른 글
| [c++] Coin Combinations(동전 조합 알고리즘, 순서 고려 X) with Dynamic Programming (1) | 2024.12.16 |
|---|---|
| [c++] BFS/DFS 구현하기 (넓이우선탐색, 깊이우선탐색) (0) | 2024.12.16 |
| [c++] MaxHeapify, BuildMaxHeap으로 HeapSort 구현하기 (2) | 2024.12.13 |
| [c++] Find the Hub 문제 Floyd-Warshall Algorithm & Bellman-Ford Algorithm으로 해결 (1) | 2024.12.06 |
| [c++] Height Order 문제 해결하기 (Floyd-Warshall's Algorithm, Topological Sort) (2) | 2024.12.05 |