이 게시글은
서울대학교 데이터사이언스대학원
조요한 교수님의
데이터사이언스 응용을 위한 컴퓨팅 강의를
학습을 위해 재구성하였습니다.
중간고사가 지나고 이전까지는 기본적인
c++에 대해서 공부했다면
이제부터는 알고리즘에 대해서 공부를한다고한다
그 첫 시간인 Heaps and Priority Queues
나에게도 처음들어보는 개념들이
조금 있었어서 다른 수업들보다는
더 공부를 해야겠다는 생각이 들었다
우선 Heap과 Prioirty Queue를
배우기전에 기본적으로 알아야하는
Binary Tree의 개념에 대해 알아보자
Binary Tree

우선 Binary Tree에 대해 알아보자
한국어로는 이진트리이다
이진트리는 위 ppt 그림과 같이
최대 2개의 자식노드를 가질 수 있는 트리구조이다
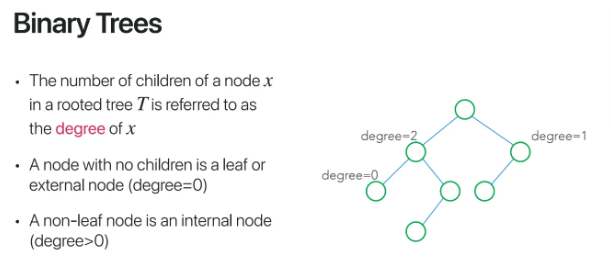
한 node가 갖고있는 자식의 개수를
degree라고 부른다
자식이 없으면 degree = 0
자식이 1개이면 degree = 1
자식이 2개이면 degree = 2
가 된다

Tree에는 Depth, Height, Level이라는
개념이 있다
Depth는 root node에서
어떤 node x까지의 거리를 뜻한다
Height는 node와 tree로 나뉠 수 있는데
height of node는
root node에서
어떤 node x까지의 가장 긴 거리를 뜻 한다
height of tree는
root에서 가장 멀리있는 leaf node까지의
거리를 뜻한다
마지막으로 Level은
같은 depth를 가진 node들의 집합을 뜻한다
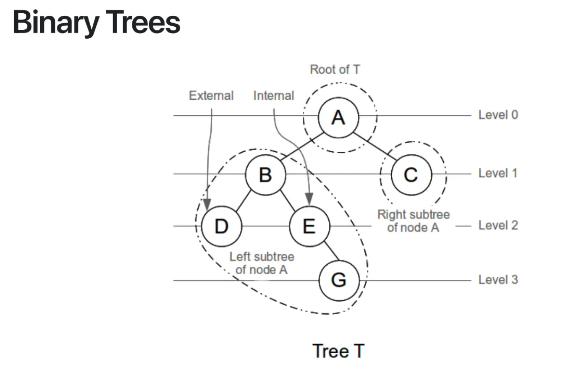
위 ppt tree를 보며 다시 용어를 복습해보자
Tree T가 위와같이 있다고 했을 때
A노드는 root
D, G, C는 children node가 없으므로
leaf node 혹은 external node라고 부른다
B와 C는 자식이 있으므로
internal node라고 부른다

binary tree를 코드로 구현하면
이렇게된다
C언어에서는 struct로
class를 쓸 수 있는 c++같은 언어에서는
class로 Node를 정의해준다
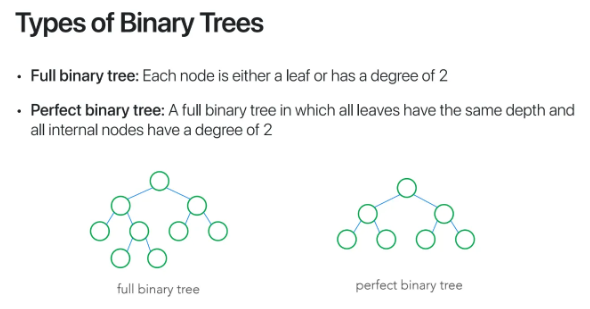
Binary Tree의 종류에 대해 보자
full binary tree란
node들이 아예 자식이 없는 Leaf node이거나
무조건 2개의 child를 가진 node들이어야한다
perfect binary tree란
full binary tree인데
모든 Leaf node들이 같은 depth에 위치해야한다
사실상 이 친구를 이해하기위해
Binary Tree의 개념을 설명한 것이다
정말 중요한 개념인
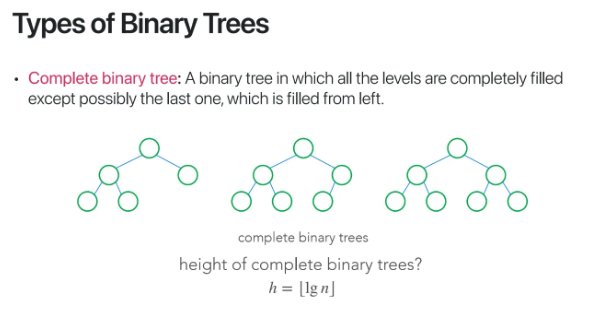
Complete Binary Tree에 대해 알아보자
한국어로는 완전이진트리라고 부르는
Complete Binary Tree는
마지막 줄이 꽉 차있거나
만약 다 차있지 않으려면 왼쪽에서부터 차있는
Tree를 말한다
이런 complete binary tree의 높이는
전체 노드 개수의 log씌운 값의 floor값이 된다
Max Heaps
이런 Complete Binary Tree같은 구조가
중요한 이유는 이러한 구조를 사용하면
빠른 탐색 및 효율적인 메모리 사용이
가능하기 때문이다
그렇다면 Complete Binary Tree 구조를 사용한
Max Heaps에 대해 알아보자
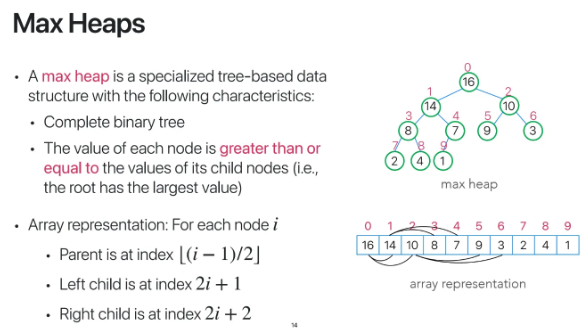
Max Heaps는
Complete Binary Tree인데
특정 노드는 모든 자손 노드들보다
크거나 같은 값을 갖고 있어야한다
그렇다면 root node는 당연히
Tree의 모든 Node 값들 중
가장 큰 값이 될 것이다
보통 이런 Complete Binary Tree의 구조는
array로 쉽게 표현이 가능하기때문에
배열로 많이 구현한다
각 노드를 왼쪽부터 index를 매겨서
배열에 저장한다
이렇게 배열에 index를 부여해서
각 노드의 값들을 저장하면
parent나 자손 node의 인덱스를
쉽게 구할 수 있다


max heap의 구조가 아닌 tree를
max heap의 구조로 만들어주는 것을
max heapify라고 한다

위 예시를 잘 보면 지금 4가
max heap의 구조를 만족시키지 못하고 있다
따라서 4를 자손 노드랑 교체를 해줘서
max heapify를 시켜주려고한다
자손으로 14와 7이 있는데
상식적으로 생각했을 때 작은 값보다는
큰 값과 교체를 해주는 것이 좋을 것이다
그렇기 때문에 14와 4를 교체해준다
이렇게 교체를 해도 4의 자손노드가
4보다 큰 값이 있기 때문에 Max heap을 만족시키지못한다
따라서 2와 8 중에서 4보다 큰
8과 다시 교체를 시켜준다

이러한 max heapify를 pseudo code로 구현해보자
max_heapify(A, 1)이란
tree A에 대해서 1번째 index에 대해
max heapify를 진행해주겠다는 뜻이다
간단하게 코드에 대한 해설을 하자면
left node와 right node를 할당해준다음
현재 가장 큰 값을 현재 Index의 노드값으로 설정해준다
그런 다음 왼쪽부터
왼쪽 자손 노드가 존재하고(l < A.heapsize)
왼쪽 자손 노드가 현재 largest의 값보다 크다면
largest를 왼쪽 자손 노드의 값으로 교체해준다
오른쪽 노드에 대해서도 마찬가지
그렇게 각 자손 노드에 대해 해준다음
계속 밑으로 내려가면서
recursive하게 Max_heapify를 호출해준다

모든 알고리즘에는 time complexity가 중요하다
알고리즘의 성능을 측정하는 중요한 지표가 되기 때문이다
max heapify의
time complexity를 알아보자
i번째 노드의 왼쪽 자식과 오른쪽 자식 노드를
비교하는 과정은 constant time에 가능하다
노드의 개수가 소요 시간에
영향을 주지 않는다는 말이다
이 알고리즘에서 시간을 좌우하는건
recursive하게 호출하는 부분이다
밑으로 내려가면서 계속해서 max_heapify를
호출해주는 과정에서
이 recursive call을 최대 몇 번까지 할 것인지가
time complexity를 결정하고
결국 worst case는 전체 Height를 다 도는 것이기 때문에
O(log n)이 되는 것이다
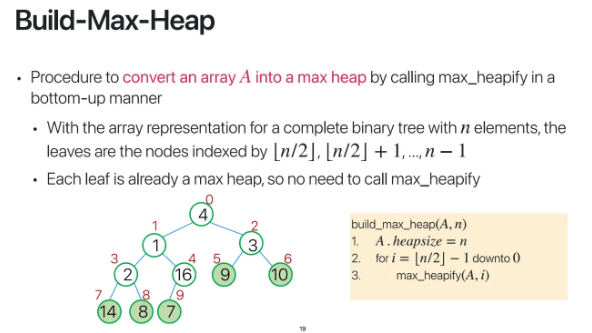
그렇다면 이런 max_heapify 알고리즘을 이용해서
array를 max heap으로 만들어보자
이는 아래에서부터 위로 올라나가며 고쳐가는 방식으로
max_heapify를 해주는데
위 pseudo code를 보면
n/2 - 1번째 노드부터 해주고 있는 모습을 볼 수있다
이는 자식 노드가 있는 노드여야
max heapify를 할 수 있기 때문에
가장 마지막 internal node를 찾아준 것이다
n/2 - 1번째 노드부터 0번째까지 돌면서
max_heapfiy를 해준다
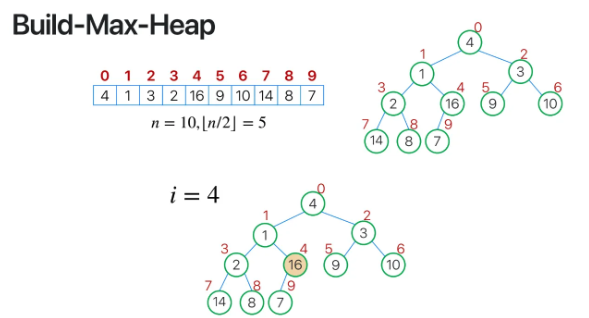
그렇다면 위 ppt 예시를 통해서
배열을 max heap으로 만드는 과정을 알아보자
총 10개의 node가 있으므로
가장 마지막 internal node는 10 / 2 - 1 = 4번째 노드가 된다
따라서 4번째 인덱스 노드에 대하여 max heapify
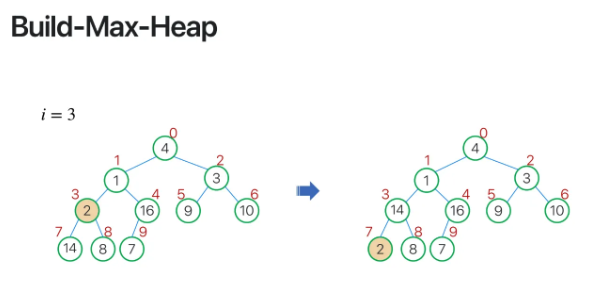
3번째 노드에 대해서..
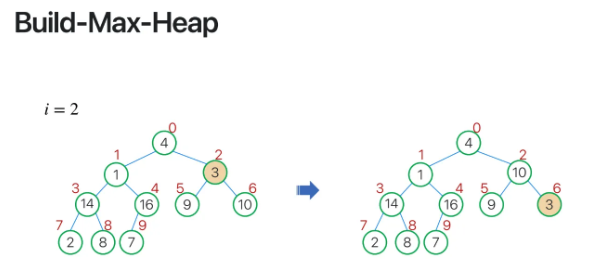
2번째도 해주고
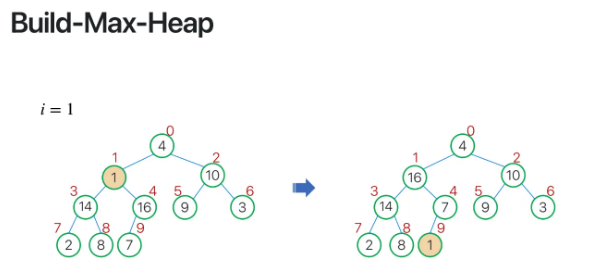
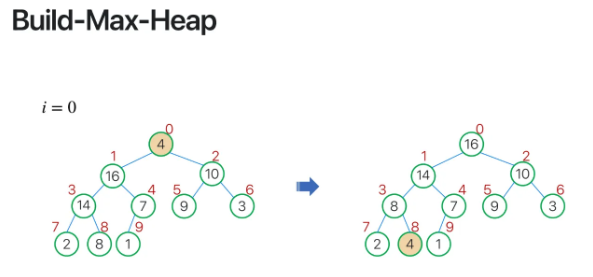
이렇게 0번째인 root node까지
max heapify를 해준다

그렇다면 이런 정렬이 안된 array에서
build max heap을 할 때의
time complexity를 알아보자
아까 위에서 봤듯이
max_heapify 자체의 time complexity는
O(log n)이다
그럼 노드 n개에 대해서 max_heapify함수를
총 n번 호출하니 time complexity는
O(n log n)이 될까?
정답은 그렇지 않다
위 build_max_heap 코드만 봐도 알겠지만
n/2-1부터 0까지 호출한다
이는 노드 개수는 n개이지만
leaf 노드는 max_heapify를 호출할 일이 없기때문에
그냥 넘어갈 수 있다
비슷한 개념으로 leaf의 바로 윗단계 노드에서는
max_heapify가 1번씩만 호출된다
그리고 그 윗단계에서는 2번씩
이렇게 root노드로 갈수록 한 노드당 max_heapify를
호출하는 횟수는 증가하지만
root로 갈수록 같은 depth에 있는 노드의 개수는 작아진다
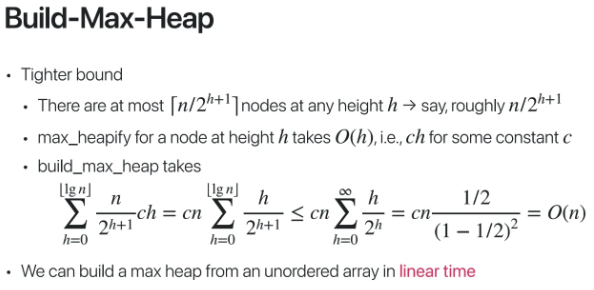
Complete Binary Tree의 경우
높이 h를 통해 전체 노드의 총 개수를 대략적으로 계산할 수 있다
계산하는 과정은
height가 0일 때 height=0에 있는 node는
root 밖에 없기 때문에 1개가 된다 (2의 0제곱)
height가 1일 때, 해당 높이에는
최대 2개의 node가 있을 수 있다 (2의 1제곱)
height가 2일 때는, 해당 높이에는
최대 4개의 node가 있을 수 있다 (2의 2제곱)
이렇게 height가 증가함에 따라
각 height에 올 수 있는 최대 node수는
2의 h제곱이고
tree의 총 최대 노드 개수는
공비가 2인 등비수열의 합이라는 것을 알 수 있다
따라서 등비수열의 합 공식에 따라
총 노드의 개수인 n은
최대 2의 h+1제곱 -1이 된다는 것을 알 수 있다
하지만 각 height에서 노드가 2의 h제곱만큼 있을 수 있다는 것은
말 그대로 최댓값이다
예를 들어 만약 전체 노드의 개수가 10개라면
전체 height는 3이 될 것이고
우리는 이러한 정보를 바탕으로
height가 1일 때는 2개
height가 3일 때는 7개의 노드가 있다는 것을
계산을 통해 유추할 수 있다
따라서 결국 전체 노드의 개수 n에 따라서
각 height에 있는 노드의 개수는 달라질 수 있다
따라서 이러한 비례관계를 이용해
식을 간단화하면 ppt와 같이
h에 있는 노드의 개수는
n/2의 h+1제곱의 floor값이 되고
어차피 Big O로 나타내야하므로
floor를 없애고 n/2의 h+1제곱으로
근사치를 책정해준다

그런 다음 height h에 있는 노드에서
max_heapify를 할 경우
time complexity는 O(h)가 된다
그렇다면 이걸 어떤 상수 c와 곱해서
ch라고 표현해주자

그래서 build_max_heap의 함수에
걸리는 최대 시간은
각 height만큼(0부터 log n까지)만큼
해당 층 최대 노드의 개수 * ch가 될 것이다
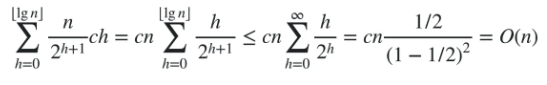
이를 이쁘게 정리한 다음
h를 무한대만큼 더한 공식을 정리해보면
위와 같은 공식이 나오고
결국 build_max_heap의 time complexity는
O(n)이 나온다고 한다
결국 array 요소의 개수에 따라 선형적으로
수행 시간이 증가함을 알 수 있다
Heap Sort와
Priority Queue에 대한 내용은
다음 게시글에 ..-!