이 게시글은
서울대학교 데이터사이언스대학원
조요한 교수님의
데이터사이언스 응용을 위한 컴퓨팅 강의를
학습을 위해 재구성하였습니다.
이번 시간에는 graph와 tree에 대한
기본 용어 및 개념 복습곽
Minimum Spanning Tree, 그리고
이를 찾는 대표적인 알고리즘인
Prim's Algorithm과
Kruskal's Algorithm에 대해 정리해보려고한다
Graph

graph에 대한 기본 개념 복습니다
rechable -> 정점 u에서 정점 v까지 path가 존재
connected graph -> 모든 vertex가 다른 모든 vertex로부터 Rechable한 graph
connected component -> 두 connected graph가 있는데 서로 연결하는 path가 없음
completed graph -> 모든 vertex들이 모두 직접 연결되어있는 graph

cycle -> 한 path에서 시작 vertex와 끝 vertex가 동일한 것
Acyclic graph -> 어떠한 cycle도 존재하지 않는 grahp
loop -> 어떤 vertex의 edge가 자기 자신을 가리키는 edge
parallel edge -> 동일한 두 쌍의 vertex를 연결하는 서로 다른 edge
simple graph -> loop이나 parallel edge가 존재하지 않는 graph
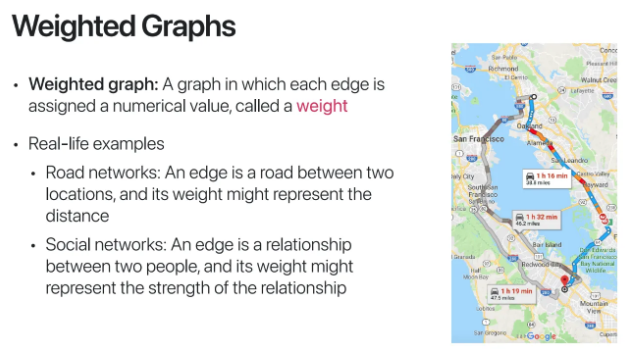
각각의 edge에 weight가 부여된 graph
실제로 도로 네트워크, social 네트워크에서 자주 사용된다
Tree

모든 tree는 기본적으로 graph이다
tree의 특징은
connected graph이고
cycle이 존재하지 않으며
보통 undirected하다는 것이다

Tree들의 set을 Forest라고 한다

Graph를 표현하는 방법이다
대표적으로 3개가 있다
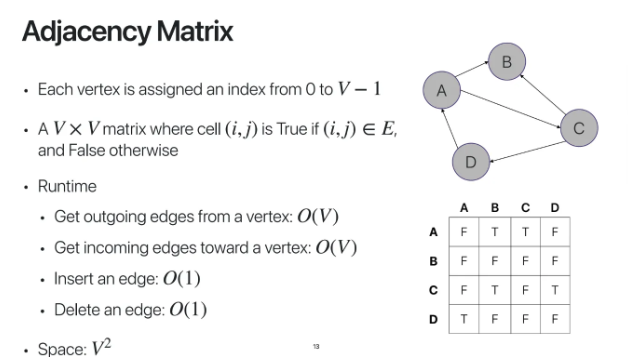
Adjacency Matrix이다
각각의 vertex에 index를 부여한다
V는 vertex의 개수이고
V x V matrix로 graph를 표현한다
각각의 row와 column은 vertex를 가리킨다
matrix에서 (i, j)에 edge가 존재하면
true를, 없으면 false를 부여한다
row가 출발점, column이 도착점이다
outgoing, incoming edge모두
vertex를 모두 탐색하므로 time complexity는
O(v)가 된다
insert, delete그냥 넣고 지우고하면 되므로 O(1)
space는 모든 vertex들을 행렬로 저장하므로
O(v제곱)만큼 걸린다
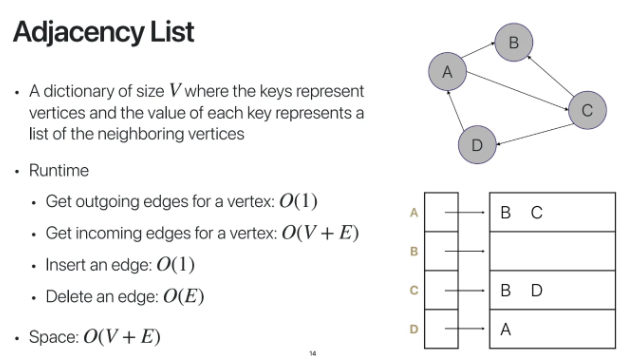
Adjacency List이다
dictionary 자료구조를 사용한다
dictionary의 k가 시작 vertex이므로
총 vertex의 크기는 dicionary key의 size이다
outgoing edge를 탐색하려면
탐색할 한개의 vertex만 접근하면 되므로
O(1)만큼의 시간이 걸린다
하지만 incoming edge를 탐색하기가 곤란한데
모든 key에 접근한 뒤, 각각의 edge를
모두 scanning을 해야한다
따라서 time complexity는
key의 개수 V와 edge의 개수 E인
O(V+E)가 된다
insert는 그냥 key를 찾아서 넣어주면되지만
delete는 key를 찾은 다음 해당 edge를 찾아야하기때문에
O(E)만큼이 소요되고
공간은 key와 edge가 저장되어야하므로
O(V+E)가 된다
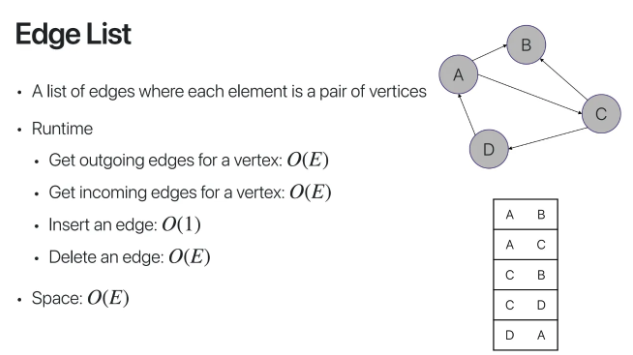
마지막으로 Edge List이다
각각의 edge를 pair로 나타낸다
그리고 그걸 List 형태로 저장한다
outgoing과 incoming 모두
결국 모든 list를 다 탐색해야하는데
list의 개수는 모든 edge의 개수이므로
시간 복잡도는 O(E)
insert는 그냥 하면되지만
delete는 list 전체를 탐색해서 지워야하므로 O(E)
모든 edge를 list에 담아 저장하므로 공간도 O(E)가 된다

넓이 우선 탐색의 pseudo code이다
사실 넓이 우선 탐색은 이전에도 봤었고
중요하지만 모두가 안다고 가정해서 간단하게 보고 넘어갔다
위 코드가 조금 특이한 점은
보통의 넓이 우선 탐색같은 경우
방문한 node와 그렇지 않은 node를
true, false로 저장하는데
위 코드의 경우 색상을 변경해주는 방식으로
작성된 것을 볼 수 있다
넓이 우선 탐색은 queue 자료 구조를 사용한다

다음은 깊이 우선 탐색
이도 모두가 안다고 생각하고 간단하게만 봤다
위 넓이 우선 탐색과 동일하게
노드의 색상을 변경하는 방식으로
방문 node 여부를 표현해주었다
깊이 우선 탐색의 경우
stack 자료구조를 사용하고
recursive하게 구현된다
Minimum Spanning Tree (MST)
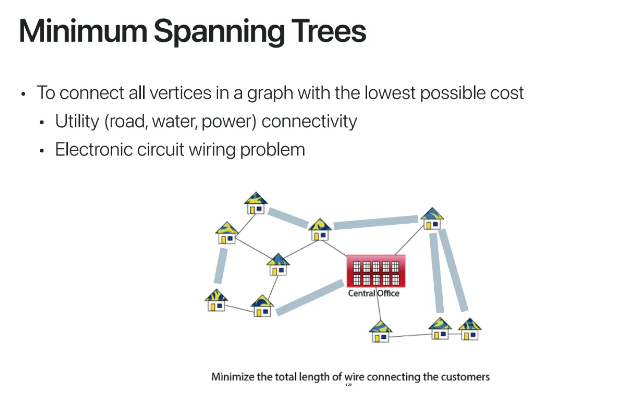
이제 오늘의 하이라이트 minimum spanning tree이다
graph에서 어떤 vertex에서 다른 vertex로
path가 존재하도록 연결하고 싶은데
이를 가장 낮은 cost로 연결하는 것이다
graph에서 cycle이 생기는 순간
당연히 그 path는 최소 비용이 아니게 된다
그래서 당연히 cycle이 없는 경로를 찾아야하고
graph의 구조는 edge에 weight가 저장된
weighted graph의 형태가 된다
path를 연결할 때는 따라서
weight의 합이 최소가 되게 연결해야한다

vertex G를 포함한 그래프 G에서
아래의 조건
1. 모든 vertex가 연결
2. cycle이 없음
을 만족시키는 tree를 spanning tree라고 한다
따라서 위 ppt의 graph에서는
아래 3개의 spanning tree가 나온다
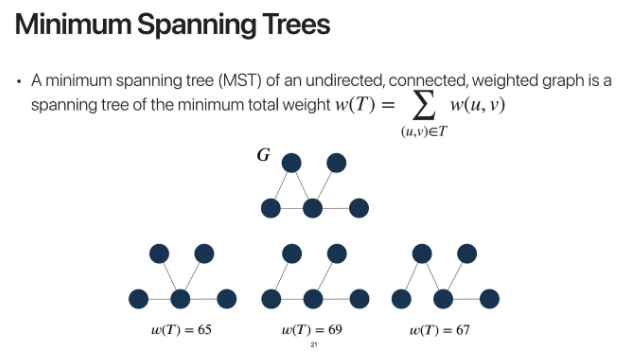
minimum spanning tree란
이런 어떤 Graph의 spanning tree들 중에서
weight의 합이 가장 작은 tree를 말한다

따라서 MST Problem이란
graph G에서 Minimum Spanning Tree를 찾는 문제를 말하고
가장 대표적인 알고리즘으로는
Prim's algorithm
Kruskal's algorithm이 있다
Prim's Algorithm

먼저 prim's algorithm을 살펴보려한다
graph G는 connected, weighted, undirected graph이다
우선 시작점으로는 random vertex를 골라서
뻗어나갈 수 있는 후보들 중
weight가 가장 작은 edge를 선택한다
위 과정을 반복적으로 수행하는데
다음 edge를 선택하는 과정에서
path가 tree의 속성을 위반하면 안된다
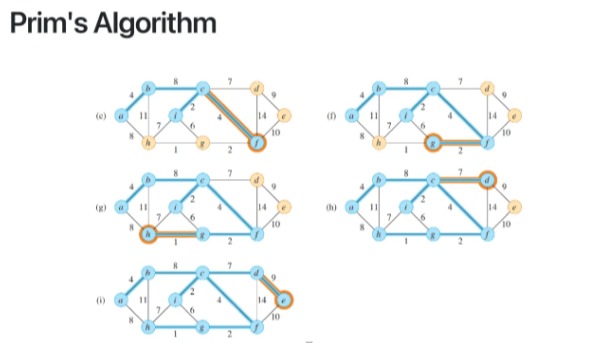
cycle이 생기면 minimum이 될 수 없을뿐더러
tree property를 위반한다
따라서 최소 weight를 따라가다가
cycle이 발생하게되면
그 edge는 버리고 다음으로 작은 weight의 edge를 고른다

Prim's Algorithm의 증명이다
증명을 하다보면 사실 너무 당연..?해서
내가 제대로 이해한게 맞나 싶었지만..
일단 내가 이해한대로 정리..
최소 weight의 edge를 선택하지 않는다고
가정해서 그 가정이 모순임을 증명하는 방식이다
여기서 cut이 나오는데 cut은 partition의 개념이다
cut은 전체 Vertex를 2개로 쪼개는 boundary 개념으로
여기서는 a와 a가 아닌 다른 vertex들을
cut으로 나누고있다
vertex a를 시작점으로 골랐을 때
다른 vertex까지 가는 edge는 총 2개가 있다
4와 8이 있는데, 그 중 만약 4가 없다고 가정하는 것이다
그럼 당연히 8의 edge를 선택하게 될 것이고
8의 edge를 따라 minimum spanning tree를 그린다
그런데 a에서 b로가는 4 weighted edge를
선택해도 minimum spanning tree가 나오는데
당연히 8보다 4로 해주는게 총 weight가 덜 나온다
따라서 처음의 가정이 모순이 된다는 것이다

prim's algorithm의 pseudo code이다
key가 weight를 뜻하고 모든 weight를 무한대로
설정한 뒤, root의 weight만 0으로 설정한다
Q는 min-priority queue인데
weight가 작은 순서대로 빨리 나가는 queue이다
이렇게 설정한 다음 모든 vertex를
queue에 넣으면 weight가 0인 root가
가장 상위에 올라오게 될 것이다
그런 다음 queue에 element들이
하나도 없어질때까지 while문을 돌면서
인접한 vertex들을 방문한다
인접한 vertex가 queue에 속해있고
weight가 가장 작은 것을 찾아서
그 vertex를 넣어주고
Queue에서 제거한다

Prim's Algorithm의 time complexity를 보자
맨 처음 v를 무한대로 초기화해주고
min-priority queue를 생성하는게 각각 O(v)
그리고 엣지에 대하여 update해주는게 E번
decrease_key 해주는게 O(log v)이므로
총 time complexity는
E * O(log v)가 된다
Kruskal Algorithm
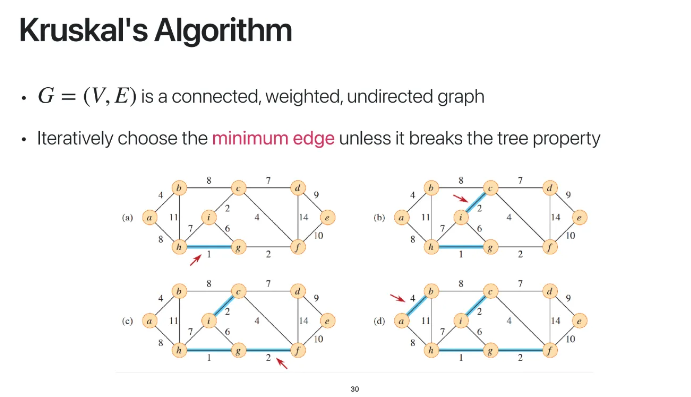
이제 다음으로 Kruskal algorithm에 대해 알아보자
graph의 가정은 동일하다
kruskal 알고리즘은 전체에서 weight가
작은 순서대로 edge를 고른다
그러다가 cycle이 생기면 그 edge는 버리고
다음으로 weight가 작은 edge를 고르는 것이다
prim's가 하나하나 순차적으로 진행하는 느낌이라면
kruskal은 우선 weight가 작은 edge들을 모아놓고
합치는 느낌이라고 보면 될 것 같다
파편화가 되어있는 것이다
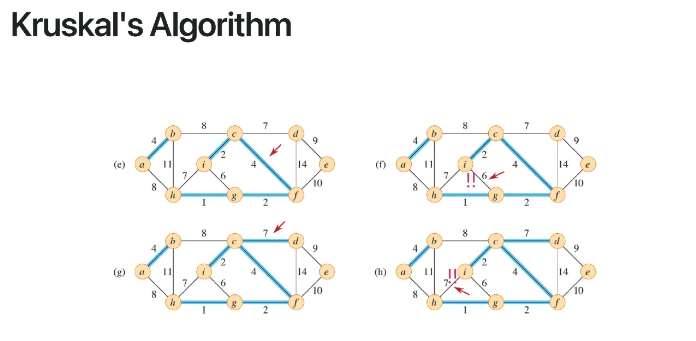
위에서부터 계속 이렇게 진행을 하다가
f에서 다음으로 작은 weight인 6을 선택하면
cycle이 생긴다
그럼 그 6을 버리고 다음으로 작은 7 edge를 선택한다
h에서도 마찬가지
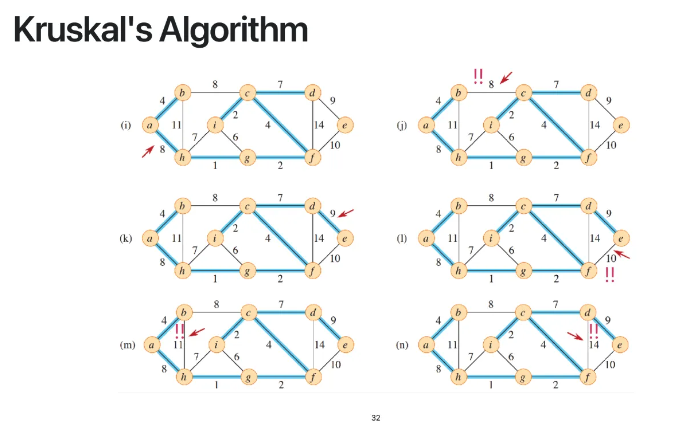
이런식으로 계속 골라가다보면
결국 모든 vertex를 탐색하게 될텐데
그게 바로 minimum spanning tree가 되는 것이다
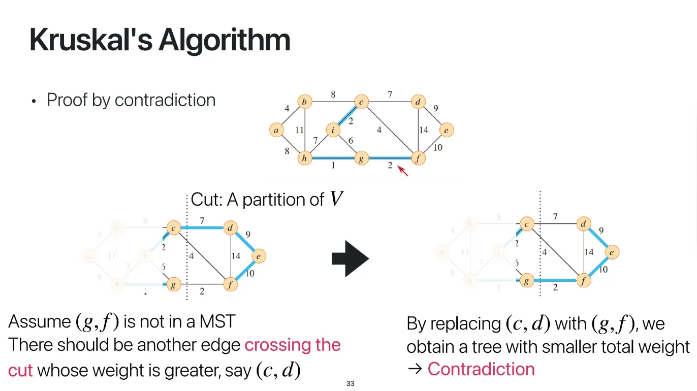
kruskal algorithm의 증명이다
prim's algorithm의 정의와 매우 유사하다
위 ppt와 같이 cut을 한 다음
(g, f)가 없다고 가정을 한다
그럼 (g, f)가 아닌 (c, f)혹은 (c, d)가
다음 edge로 선택이 될 것이다
하지만 (c, f)나 (c, d)보다
(g ,f)를 선택하는게 당연히 더 weight가
적어지므로 가정에 모순이 생긴다
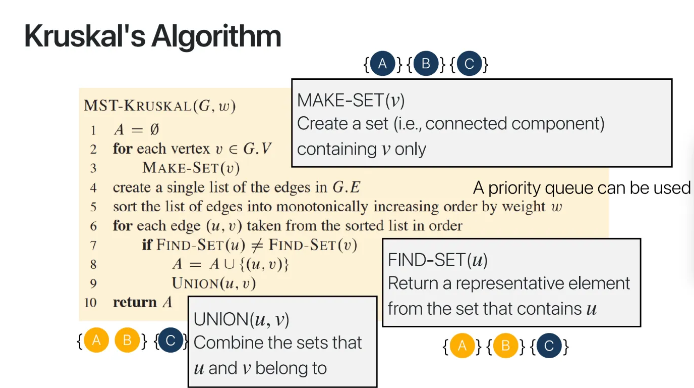
kruskal algorithm의 pseudo code이다
옛날에 이산수학 공부할 때 배웠었는데
다시 보니 너무 새롭다 ㅎㅎ..
모든 vertex에 대해서 set을 만들고
edge들을 weight의 increasing order로 정렬한다
그다음 6, 7, 8에서는 cycle이 있는지를 확인하는 부분인데
sorted list에 저장된 edge를 순서대로 돌면서
find set을 해준다
find set은 현재 vertex가 들어있는 connected component set에서
대표가 되는 vertex를 반환해주는 메소드이다
아무튼 각 vertex에 대하여 find set을 했을 때
반환되는 vertex가 같지 않다면
cycle이 없는 것이므로
합집합인 union을 해주고
만약 반환 vertex가 같다면 그냥 넘어가게된다
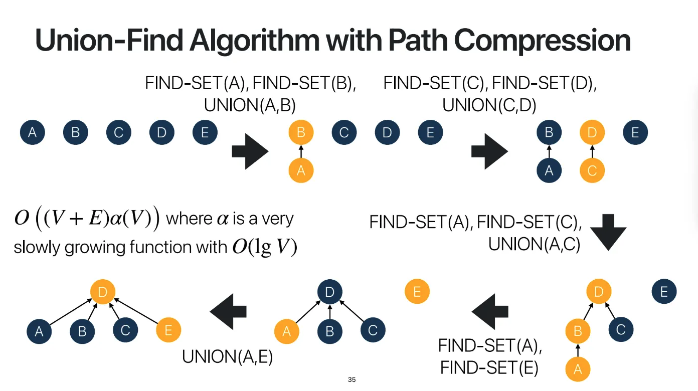
이 union하는 과정을 어떻게하면 효율적으로할까 하다가
나온 것이 바로 아주 유명한 알고리즘인 union-find 알고리즘
처음에 각각의 vertex들은
서로 다른 connected component를 이루고있다
그러다가 가장 작은 weight를 가진 edge를 골랐고
그게 A vertex와 연결된 edge였다
find-set(A), find-set(B)를 한 결과
이상이 없었기에 union(A, B)를 해준다
이 Union하는 과정에서
A를 B의 child로 연결해줬다
이렇게 되면 이 connected component의
대표 vertex는 B가 되는 것이다
그다음 계속해서 다음 edge를 찾고
find-set, union과정을 반복해준다
set과 set을 union할 때는
개수 혹은 높이가 적은 set을
개수 혹은 높이가 많은 set에 붙여준다
그런데 이 과정을 반복하면서 set의 tree구조가 깊어지다보면
find-set에서 대표 노드를 찾기가 시간이 많이 걸린다
이를 효율적으로 진행하기 위해
path compression(경로 압축)을 사용한다
find 연산 시 각각의 vertex들을 부모에 direct하게
연결해줌으로써 탐색에 걸리는 시간을 줄이게 된다

time complexity를 정리해보자
맨 처음 connected component set을 만드는건
총 Vertex의 개수만큼 시간이 소요되고
weight순으로 edge list를 sorting하는 것은
O(E log E)만큼 소요되는데
connected graph의 특성 상
edge의 개수 E는 vertex의 개수 V-1보다
작거나 같을 수 밖에 없다
따라서 Big-o 표기법에서는
O(log E)는 O(log V)로도 사용이 가능하고
O(E log E) = O(E log V)가 될 수 있는 것이다
그다음 union-find를 실행하는데 시간은
O(E log V)가 나온다
따라서 총 time complexity는
O(E log V)가 된다
'강의 > computer programming' 카테고리의 다른 글
| [computer science] Dynamic Programming (동적 프로그래밍) (1) | 2024.11.20 |
|---|---|
| [computer science] Red-Black Tree (1) | 2024.11.18 |
| [computer science] Heap Sort와 Priority Queue (2) | 2024.11.10 |
| [computer science] Binary Tree, Max Heap (1) | 2024.11.08 |
| [Computer Science/c++] Type Casting과 Exception Handling (0) | 2024.10.26 |