이 게시글은
서울대학교 데이터사이언스대학원
조요한 교수님의
데이터사이언스 응용을 위한 컴퓨팅 강의를
학습을 위해 재구성하였습니다.
이번시간에 배운 내용은
Red-Black Tree..
지금까지 배웠던 알고리즘과는
약간 다르게 일관된 방법이 있는게 아니라
좀 어렵고 까다롭다고 느껴질 수 있다
그래서 무작정 외우려거나 하기보다는
그냥 이런식으로 이런 문제를 해결하고자했구나
하는 관점에서 차근차근 정리를 해보려했다
그럼 시작..
Binary Search Tree

일단 Red-Black Tree를 이해하기 위해선
Binary Search Tree를 기본적으로 이해하고있어야한다
Red-Black Tree는 기본적으로
binary search tree의 문제점을
해결하기위해서 나온 것이기 때문이다
Binary Search Tree는
각각의 node는 value를 갖고있고
최대 2개의 child node를 갖고있으며
어떤 node의 왼쪽의 모든 subtree의 값들보다
node의 value가 커야하고
오른쪽에 있는 subtree들보다는 작아야한다
이렇게 node의 value에 따라
정렬을 미리 해놓기때문에
탐색에 유리한 형태이고
search, insert, delete 모두
O(log n)이 소요된다

하지만 이런 Binary Search Tree에는
치명적인 단점이 있는데
이는 tree가 unbalance하다면
worst search가 될 수 있다는 점이다
위 ppt와 같이 저장되어있는경우
binary search tree의 모든 조건을
만족시키기 때문에 binary search tree가 맞지만
그냥 array에서의 탐색과 다를 바가 없다
이러한 경우 worst-case에서
search, insert, deletion 모두
O(n)의 time complexity를 가지기때문에
binary search tree의 효율성을
누릴 수가 없게된다
Red-Black Tree
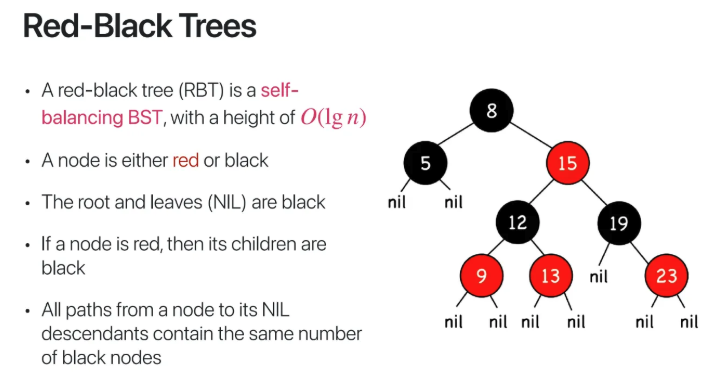
이런 Binary Search Tree의 단점을
보완하기 위해 나온 것이 Red-Black Tree이고
다른 말로는 self-balancing tree(BST)라고도 부른다
이름 그대로 binary search tree인데
스스로 balancing을 해서 불균형을 스스로 고치고
worst-case를 없애려고 하는 것이다
높이는 기본적으로 O(log n)이고
모든 노드는 red이거나 black이다
root node와 leaf node
(ppt에서 nil)은 무조건 black이고
red node들은 어디에 있어도 상관없지만
red node들이 연달아서 나올 수는 없다
즉, red node의 직계 자손들은
반드시 black이 되어야한다는 뜻이다
그런 다음
어떤 노드에서 nil까지 가는 모든 path에서
black node의 개수가 같은 것이
Red-Black Tree(RBT)의 가장 큰 특징이다
위 ppt RBT를 예시로 보면
root node인 8에서 nil로 가는 path를 보면
8-15-12-9-nil
8-15-19-23-nil
8-5-nil
8-15-12-13-nil
위 모든 path에서 black node는
2개만 나오는 것을 알 수 있다
아마 다른 path를
확인해봐도 마찬가지일 것이다

RBT는 root 노드에서 nil로 가는 모든 path에서
black node의 개수는 동일하다
또한, red node가 중간중간에 낄 수는 있지만
연달아서 나올 수는 없다
따라서 이러한 특징들을 고려했을 때,
가장 긴 path가 가장 짧은 path의
2배 이상이 절대 될 수 없다
이는 RBT의 매우 중요한 특징으로
이러한 특징으로 인해 RBT는
roughly balance가 되었다고 가정할 수 이씨는 것이다
또한, 그래서 RBT의 Height는
항상 O(log n)에 bound 될 수 밖에 없다

RBT는 여러 자료구조에서 유용하게 활용되는데
c++의 map, set에서
내부적으로 RBT로 구현이 되어있다

기본적으로 RBT에는 3가지 operation이 있는데
search, insert, delete가 있다
search의 과정은 그냥 BST와 동일하지만
insert와 delete를 좀 자세히 살펴봐야한다
위에서도 말했지만
insert와 delete의 알고리즘이
딱 한 가지로 떨어지지 않는다
경우나 상황에 따라 case by case이기 때문에
이러한 경우들을 모조리 외워야겠다보다는
그냥 balancing을 하기 위해서
어떨 때는 이렇게 해야만하고
저럴 때는 저렇게 해야만했구나 하며
그 알고리즘이 만들어지는 과정을 이해한다는 느낌으로
보면 좋을 것 같다
Rotation

우선 Insert와 delete를 보기 전에
Rotation이라는 개념을 알아야한다
subtree들을 재정렬해서
tree의 구조를 변경하는 것인데
subtree들의 balance가 맞지 않을 때
주로 많이 이용한다
위의 예시같은 경우는
5 node를 중심으로 왼쪽으로 rotation
시킨 경우이다
left와 right 2가지 방법이 있다

5 node를 중심으로 left-rotation을 시킨 것이다
5를 child로 내리고 10을 5의 부모로 만들었다
그런데 그렇게 되면 10은
5, 8, 12라는 3개의 node의 부모가 되기 때문에
5를 제외한 8, 12 중 한 개를 5의 자식으로 내려준다
이 경우에서는 8이 가능하므로
8을 5의 child로 넘겨주어
left-rotation을 완성하였다

이번엔 아까 left-rotation 시킨 그래프를
다시 10 node를 기준으로 right-rotation을 시켜보자
그럼 자식인 5가 다시 root로 올라오고
10은 5의 child가 된다
그럼 5는 2, 8, 10 3개의 자식을 갖게되므로
2와 8 중 8이 10의 child로 내려가게되었다
그래서 다시 left-rotation을 시키기 전
형태로 돌아가게 되는 것을 볼 수 있다
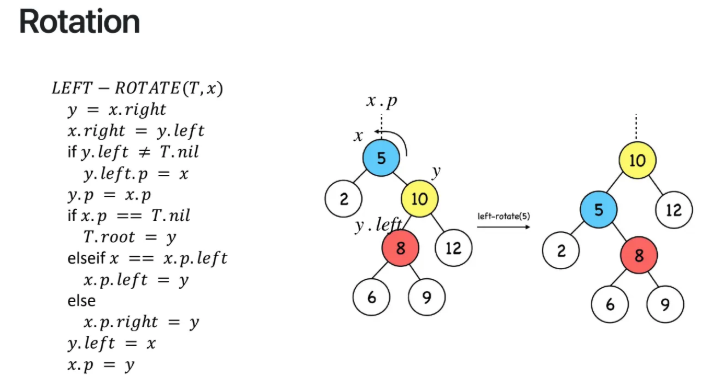
left-rotation의 pseudo code이다
left-rotation을 할 때 직접적으로
연루가 되는 노드는 5, 10, 8
이 3개 뿐인데
이 3개의 node에 대해서
정보를 update를 해주는 것이다

rotation의 time-complexity는 O(1)이다
BST의 속성을 깨뜨리지 말고
연루가 되어있는 3개의 node만 update를 해주면된다
Insertion

이제 RBT에서의 insertion을 천천히 봐보자
insertion은 크게 2가지 step으로 이루어져있는데
1. BST에 insert하는 방식으로 넣고 빨간색으로 칠하기
2. 그렇게 했을 때, RBT의 형태가 깨진다면
height balancing, color constraint 기법을 통해 fix-up하기

우선 비어있는 tree를 가정해서
insertion을 한 번 살펴보자
아무것도 없는 empty tree에
15를 insert한다
처음 넣을 때는 red로 넣는데
그렇게 되면 root는 black이어야한다는
RBT의 조건을 만족시키지 못한다
그래서 다시 red에서 black으로 바꿔준다
이렇게 되면 RBT의 조건을 모두 만족시키기때문에
insert가 끝난다

그다음에 여기에 5를 추가하려고한다
기본 BST insert방식으로 5를 넣은다음
red로 해준다
그럼 root인 15밑에 5가 child로 들어가는데
이는 모든 RBT의 조건을 만족하기때문에
fix-up 과정을 생략하고 그냥 끝낸다

그 다음에 1을 넣어보도록하자
일반 BST insert로 넣어주면
5 밑에 1이 들어가게되고 red로 칠해주는데
이렇게 되면 red가 연속으로 나오면 안된다는
RBT의 조건을 만족시키지 못한다
따라서 5 node를 중심으로 right rotation을 시켜준다
(height balancing)
이제 가운데 모양처럼 right rotation이 되었다
하지만 그래도 red가 연속으로 나오면 안된다는
RBT의 조건을 만족시키지 못한다
따라서 5와 15의 색상을 교체해준다
(color constraint)
이렇게 하면 가장 마지막 tree의 형태가 되고
RBT의 모든 조건을 만족하게 된다
이제 조금 복잡한 insert를 살펴보자
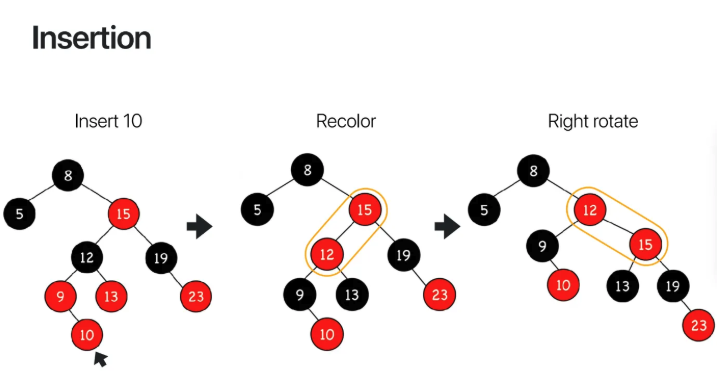
왼쪽과 같은 RBT에 10을 넣어보았다
그럼 9의 밑에 red로 들어가게 되는데
9도 red이기 때문에 RBT의 조건을 만족시키지못한다
그래서 12와 9,13의 색상을 서로 교체해줬다
하지만 그렇게 해줘도 15와 12가
red로 연속으로 이어져있기때문에
RBT의 특성을 만족시키지 못한다
따라서 12를 기준으로 right rotation을 시켜줬다
그랬더니 가장 오른쪽 그래프의 형태가 나왔는데
이렇게 해도 12와 15가 연속으로 red로 있기 때문에
RBT의 조건을 만족시키지못한다

그래서 만족시켜주기 위해서
12 node의 색상을 black으로 변경시켜준다
그렇게 되면 12와 9라는 연속적인
black node 때문에
한 node에서 nil까지 가는 path의
black node 개수는 모두 똑같다는
RBT의 속성을 또 만족시키지 못하게 된다
따라서 12를 기준으로 left rotation을 시켜준다
이렇게 되면 오른쪽과 같은 형태가 나오고
한 node로부터 nil까지 갈 때 black node의
개수가 path마다 동일하게 되는 것을 확인할 수 있다
이렇게까지 해주면 10의 insertion이
완성되는 것이다
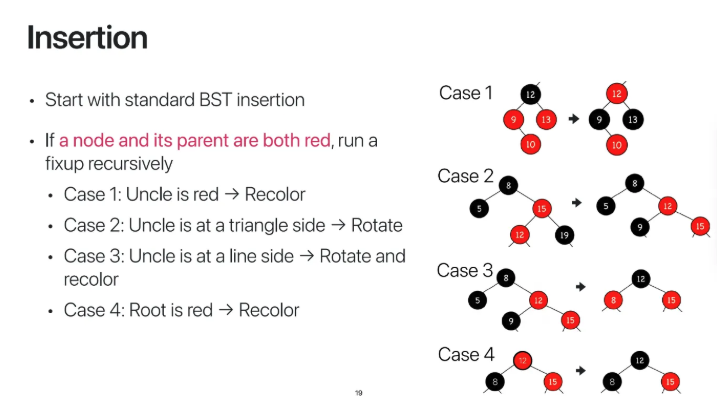
RBT의 insertion 과정을 정리해보자
우선 standard BST insertion으로 시작해서
빨간색으로 붙인다
만약 내가 넣는 node의 부모가 검은색이라면
큰 문제가 생기지 않는다
그러나 부모가 red라면 fix-up을 시켜줘야하는
상황이 발생한다
이러한 상황은 크게 4가지 case로 정리할 수 있다
CASE 1. uncle(부모 node의 다른 자식)이 red인 경우는
case1의 그림처럼 색상을 서로 교환해준다
CASE 2. uncle이 black인데 그게 triangle side(오른쪽으로 갔다가 왼쪽으로 꺾는)에
있는 경우는 right rotation을 시켜준다
CASE 3. uncle이 black인데 그게 line side(일직선 상의)에
있는 경우는 left rotation을 시켜준다
CASE 4. root가 빨간색이 되는 경우는 root의 색상을
black으로 변경해준다
이제 각 case별로 좀 더 구체적으로 살펴보자
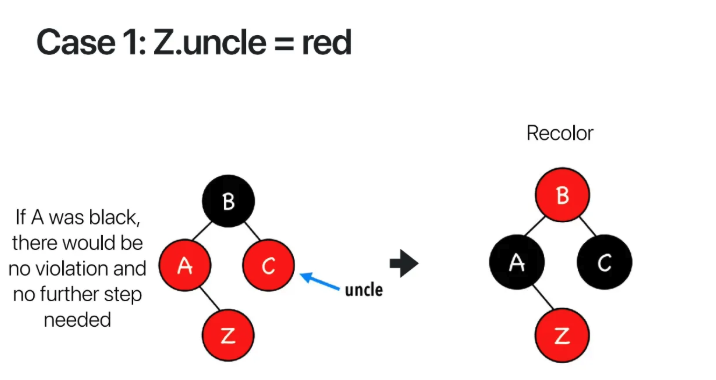
Case 1 -> uncle is red
새로 insert한 node는 Z
그리고 uncle은 C이다
이렇게 될 경우네는
parent의 색을 black으로 변경해주고
grandparent의 색을 red로 변경해준다
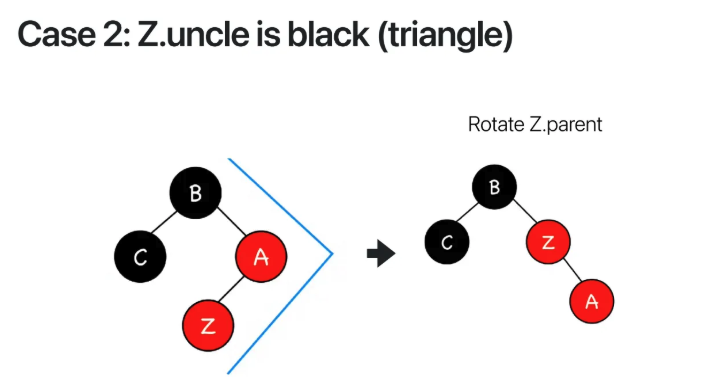
Case 2 -> uncle is black & triangle
Z와 A가 충돌이 나는데 uncle인 C가 black이고
오른쪽으로 갔다가 왼쪽으로 꺾는 triangle에 위치해있다
이럴 경우 Z의 parent를 rotate해서
triangle을 line으로 변경해준다
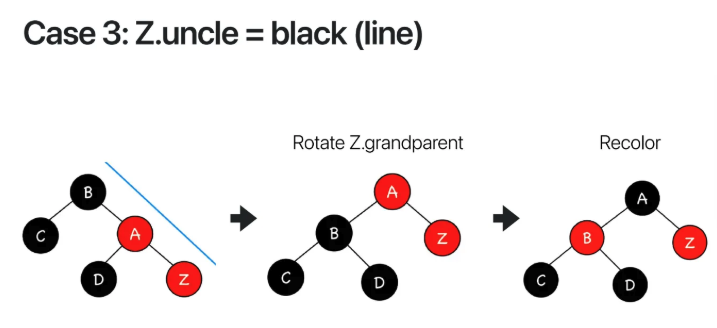
Case 3 -> uncle is black & line
Z와 A가 충돌이 나고 case2와 동일하게
uncle인 C가 black인 상황이다
이런 상황에선 Z의 할아버지인 B를 기준으로
left rotate를 시켜준다
그렇게 되면 A가 가장 위에 올라가고
Z가 그 다음으로 위치하게된다
그렇게 해도 A와 Z가 계속 충돌하므로
A의 color를 검은색으로 바꿔준다
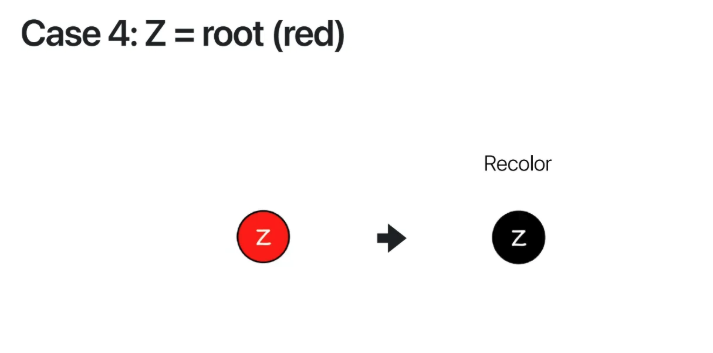
Case 4 -> root is red
이렇게 case 1, 2, 3과 같은 방식으로 수정해줘
충돌 부분이 root까지 도달했는데
root가 빨간색인 경우 black으로 변경해준다
root는 어차피 모든 Path에 영향을 미치기 때문에
검은색으로 변경해줘도 아무런 문제가 없다
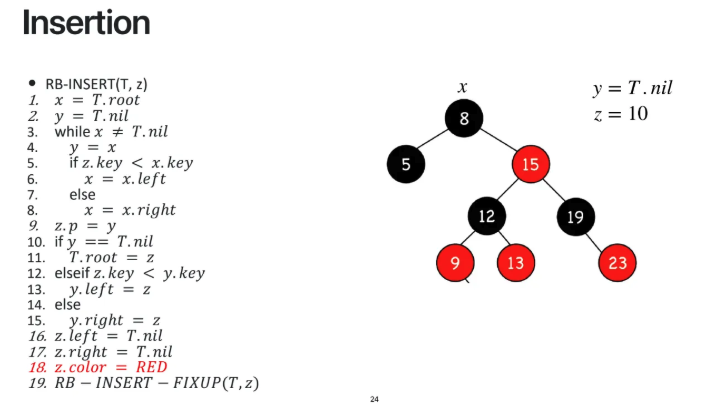
insertion의 pseudo code이다
코드를 하나하나 자세하게 뜯어보기보단
큰 그림을 이해하는 느낌으로 훑어보자
우선 이 부분은 그냥 일반 BST처럼
insert를 한 다음 fixup을 해주도록 구현한 부분이다
z=10을 넣어주려하면 9의 right child로
들어가게되는 것을 확인할 수 있을 것이다
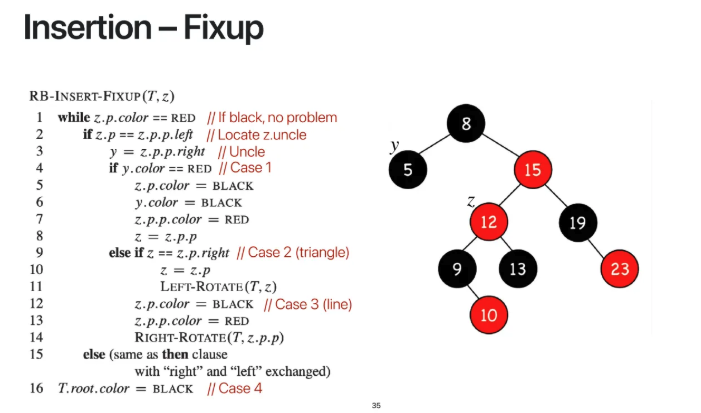
fixup 부분 구현부의 pseudo code이다
10이 9의 child로 들어왔고
uncle이 red였으므로
case 1에 따라 색상을 교체해줬다
그랬더니 12와 15에서 충돌이 발생했다
이 경우는 case2인 triangle에 해당하므로
left-rotate를 수행해준다

left rotation을 해주면 위와같이 tree가 되고
12와 15가 다시 충돌을 하는 것을 알 수 있다
그리고 이건 case 3에 해당하므로 right rotation을 해준다

그렇게 right rotation을 해주면
RBT의 모든 특성을 만족하게 되어
fixup이 종료됨을 확인할 수 있다

insertion의 time complexity를 살펴보자
BST에 insert를 할 때는 O(log n)이다
그러나 fixup이 시간을 많이 차지하게된다
사실상 while문이 계속 반복되며 여러번 돌아야하는건
생각해보면 case 1밖에 없다
나머지 case 2, 3, 4는 결국 한 번씩만 해주면 된다
그런데 case 1을 한 번 수행해서 색상을 변경해줄때마다
우리가 해결해야하는 노드의 위치가 2칸씩
올라가는 것을 확인할 수 있다
따라서 while문이 한 번 돌때마다 높이는 2칸씩 올라가서
root까지 가서 fix up을 수행하면 알고리즘이 종료되므로
fixup의 time complexity는 tree의 height에
bound되고 따라서 전체 time complexity는 O(log n)이 된다
Deletion

이제 deletion에 대해서 알아보자
어떤 node를 지우면 RBT의 형태를 깨뜨릴 수가 있다
특히 지워진 node가 black일 때
전체 path에서 black node의 개수에 영향을 줄 수 있다
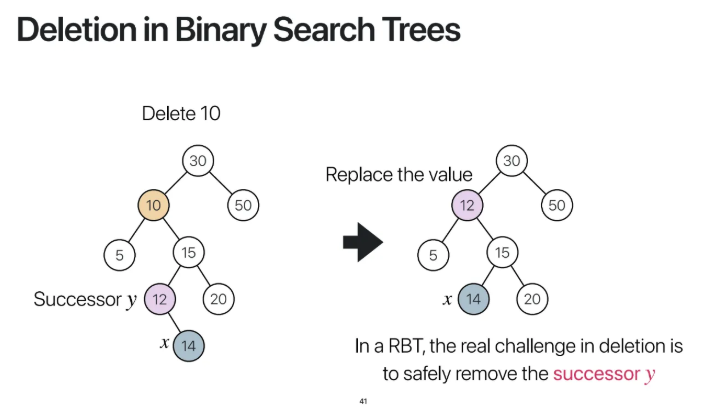
우선 기본 Binary Search Tree에서 deletion을
하는 방법부터 살펴보자
10을 delete해주고 싶다고 하자
그렇다면 binary search tree에서는
10의 successor를 찾아준다
보통 자식 노드의 왼쪽 자식을 successor로 삼는다
따라서 위 예시에서는 12가 successor가 된다
그래서 successor인 12와 지우려고하는 10을
서로 exchange 해준 다음
원래 successor node를 지워주고 그 자손들을 연결해준다
하지만 이게 delete라고 하지만
사실 코드상으로 보면 10 node를 갖고있던
data structure자체는 물리적으로 삭제되지않는다
그냥 그 값만 successor의 값으로 변경되는 것 뿐이다
원래 노드 10의 포인터 주소는 그대로 있고
그 안에 담겨있는 값만 successor의 값으로 바뀌는 것이다
따라서 RBT에서의 delete는 이러한 점을 활용한다
왜냐하면 노드의 data structure 자체가 지워지지 않는다는 것은
그 노드의 색상은 그대로라는 것인데
이미 tree가 RBT의 특성을 만족하고 있을텐데
색상을 변경해주면 다시 맞춰주는 과정이 매우 복잡해지기 때문이다

deletion도 case by case로 나뉠 수 있다
처음 case는 지우려고 하는 노드 z가
자식이 1개 밖에 없거나 아예 없을 경우이다
이 상황에서 z 노드가 red인 경우
원래 있던 자식을 그냥 z의 위치로 넘겨준다
만약 자식이 없으면 그냥 nil node가 되는 것이고
이 때는 진짜로 z 노드가 물리적으로 지워지는 것이다
z가 red 일때는 큰 문제가 생기지 않는다
왜냐하면 path에서의 black 개수에
영향을 끼치지 않기 때문이다
하지만 지우려는 노드가 black이면 문제가 발생한다
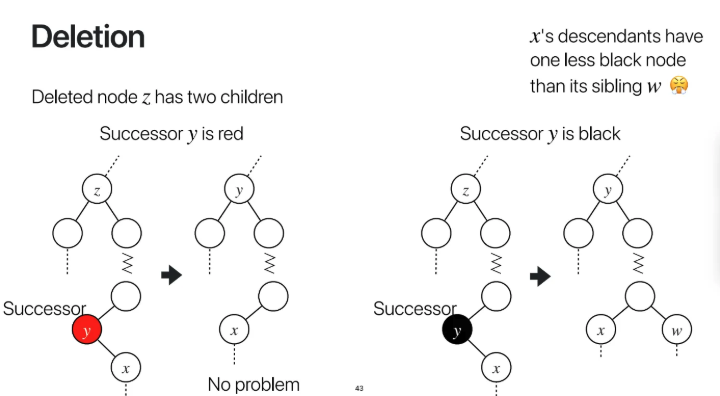
이제 삭제할 노드가 2개의 자식을 갖고있는 경우이다
successor을 찾아서 successor를 제거하고
z에 successor의 값만 넣어주는 과정이다
하지만 위와 마찬가지로
물리적으로 제거하는 node인 successor가
red이면 문제가 없지만
black이라면 문제가 생기게 된다

위의 사례에서 봤듯이
실제로 지우는 node가 red라면 아무런 문제가 없다
하지만 그렇지 않은 경우 문제가 생기게 된다
black node를 지우면 path에서의 black 개수가
줄기 때문에 문제가 생기는 것이다
따라서 deletion process의 대부분의 과정은
rebalancing을 통해서 black node의
개수를 맞춰주는 과정이라고 할 수 있다
이 deletion에서 black node의 개수를 맞춰주는 과정도
여러 case들이 존재한다
하나씩 차근차근 살펴보도록하자
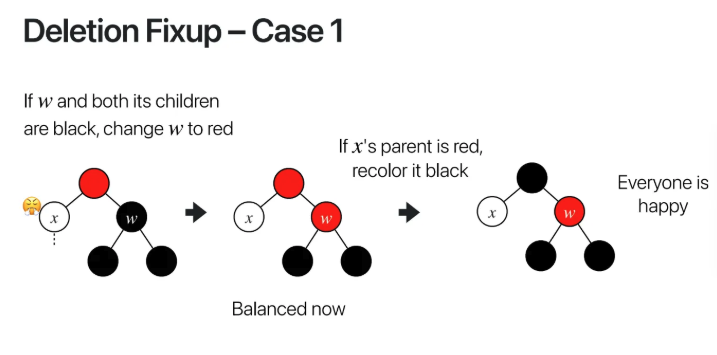
지워진 노드의 자리에 들어간 x의 형제 w가 black이라면
w를 red로 바꿔준다
하지만 부모가 빨간색이라서 충돌한다면
부모를 black으로 변경해준다
그렇게 되면 RBT의 특성을 만족하게된다
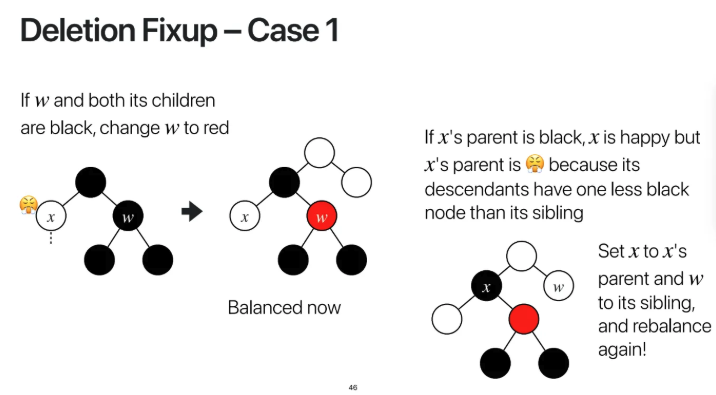
만약 x와 w의 부모가 검은색이었다고 가정하면
w를 red로 변경해준다
하지만 black을 red로 변경해주면
w의 자식들은 black node의 개수를
1개 잃어버리게 되는 것이므로
RBT의 속성을 만족시키지 못하게 된다
따라서 이럴 경우
x를 x의 parent로 다시 올리고
w를 다시 x의 형제로 만들어준다
그럼 다시 balance가 맞는 모습을 볼 수 있다
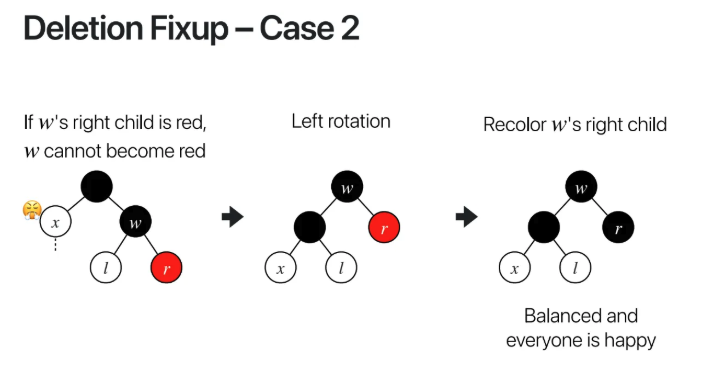
위의 경우에서는 w를 red로 변경해서 문제를 해결했다
하지만 만약 w의 child가 red라면
w를 red로 변경해주면 안된다
따라서 이럴 경우 left rotation을 시켜준다
그럼 w가 grandparent가 되고
x의 parent가 w의 child가 된다
하지만 이렇게 되면 r의 path에는
black node가 1개가 되므로
balance가 맞지 않기 때문에
r을 black으로 교체해준다
그럼 모두 균형이 맞아지는 것을 볼 수 있다
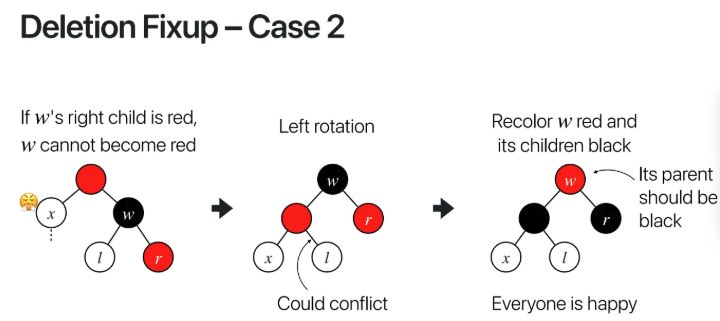
x의 부모가 red, w가 black, r이 red일 때
left rotation을 시켜준다
그렇게 되면 l이 무슨 색이냐에 따라
충돌할 가능성이 있다
따라서 x의 부모와 삼촌인 r을
black으로 칠한 다음
grandparent인 w를 red로 변경해주면
RBT의 성질을 만족시키게 된다
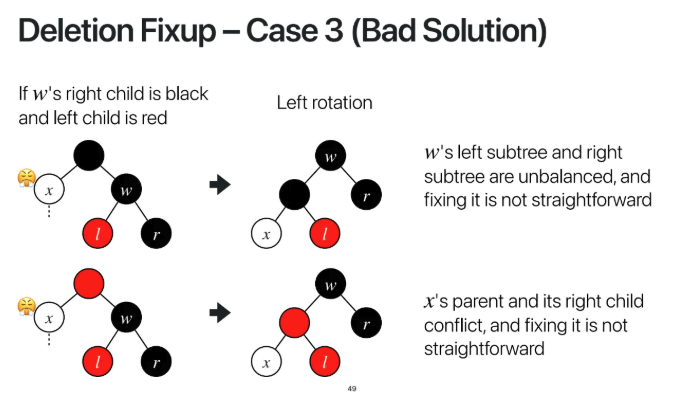
이번에는 case 3인데 잘못된 해결방법에 대해 알아보자
parent가 black, w가 black, r이 black인 경우이다
이럴 때 우선 left rotation을 해준다
그렇게 되면 w의 left subtree와 right subtree가
balance가 맞지않게되는데
이런 경우를 고치는 것은 매우 힘들다고한다
밑의 경우에도 마찬가지인데
부모가 빨간색일 때 left rotation을 하면
색상에서 충돌이 생기게 되는데
저런 경우를 해결해 주는 것이 매우 힘들다고한다
따라서 이런 case에서 left rotation을
시켜주는 것은 bad solution이 된다
그래서 이런 case는 어떻게 해결해주는지 알아보자
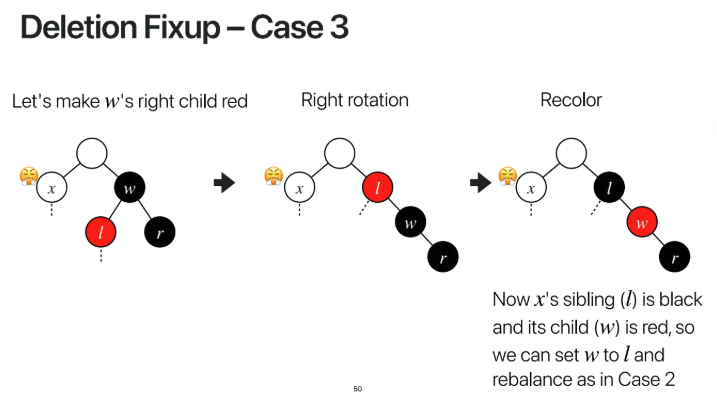
결론부터 말하자면 case 3의 경우
case 2의 상황으로 만들어서
case 2의 해결법으로 해결을 해주게된다
따라서 case3의 경우 우선 right rotation을 시켜준다
그런 다음 l을 black으로
w를 red로 색상을 변경시켜준다
case2처럼 만들어주기 위해서
두 노드의 색상을 변경시켜주는 것이다
그렇게 하면 case2의 형태로 만들어줄 수 있으니
case2의 해결방법대로 풀면된다

마지막 case 4이다
w가 red일 때 left rotation을 해준다
그럼 w가 위로 올라가고
w의 원래 parent가 아래로 내려가게된다
그렇게 되면 a가 부모의 오른쪽 자식으로 오게되는데
path에 imbalance가 생긴다
따라서 parent와 w의 색상을 변경해준다
이렇게 되면 앞의 case 1, 2, 3 중 한 개의 case가 되고
해당 case의 해결방법을 통해 문제를 풀 수 있다

deletion의 pseudo code이다
코드를 하나하나 자세하게 보지는 않겠다
우선 이 부분은 일반 BST의
node delete 부분이다
그런 다음 RB-DELETE-FIXUP을
시켜주는 것을 볼 수 있다

이 부분이 RBT deletion의 핵심이라고 할 수 있는
fix up 부분이다
차근차근 읽어서 이해해보면 좋을 것 같다

마지막으로 deletion의 time complexity를 보고
힘들었던 오늘 강의 복습을 마쳐보려고한다..
우선 BST deletion의 time complexity는
O(log n)이다
중요한건 fixup의 time complexity인데
case 2, 3의 경우는 O(1),
case 1의 경우도 O(1),
case 4의 경우 fixup 자체는 O(1)인데
rotation을 시키면 node가 한 칸 떨어질 수가 있다
그 다음에 case 1, 2, 3 중에 하나로 fixup을
시켜줘야하는데 그렇게 하면 2칸을 다시 올라가는게
guarantee 된다고 한다
그래서 결론적으로는 총 time complexity는
O(log n) 안에 끝낼 수가 있다고 한다
이렇게 약간 .. 조금 많이 힘들었던
Red Black Tree 강의 정리 마무리-!
'강의 > computer programming' 카테고리의 다른 글
| [computer science] Dijkstra's algorithm (다익스트라 알고리즘, single-source shortest paths(1)) (0) | 2024.11.26 |
|---|---|
| [computer science] Dynamic Programming (동적 프로그래밍) (1) | 2024.11.20 |
| [computer science] Graph, Tree, Minimum Spanning Tree(Prim's, Kruskal's Algorithm) (1) | 2024.11.11 |
| [computer science] Heap Sort와 Priority Queue (2) | 2024.11.10 |
| [computer science] Binary Tree, Max Heap (1) | 2024.11.08 |