이 게시글은
서울대학교 데이터사이언스대학원
조요한 교수님의
데이터사이언스 응용을 위한 컴퓨팅 강의를
학습을 위해 재구성하였습니다.
이 번 시간은 single-source shortest paths의
첫 번째 강의 내용에 대해서 정리를 해보려고한다
주된 내용은 Dijkstra(다익스트라) 알고리즘이었다
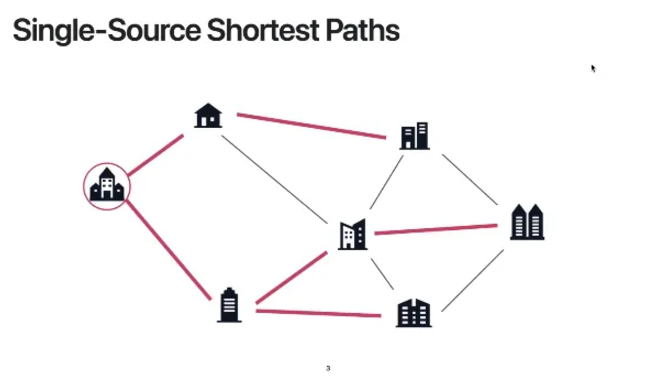
다익스트라는 대표적인 single-source shortest path 알고리즘이다
single-source shortest path의 가장 대표적인 예시는 위의 상황이다
마을이 7개의 건물이 있고 가장 왼쪽에 우체국이 있다고 할 때
각각의 집에 방문할 수 있는 가장 짧은 path는 무엇일까

일반적으로 single-source shortest path는
weighted, directed graph에서 path를 찾는 알고리즘이다
출발점인 source vertex를 s라고 할 때
s에서 모든 vertex들을 지나가는 가장 짧은 경로를
single-source shortest path라고 한다
가장 짧은 경로라는 것은
path 상의 weight들의 합이 가장 작은 것을 뜻하고
source vertex에서 도달을 못하는 vertex가 있다면
그 weight는 무한대라고 가정한다
그리고 single-source shortest path는
반드시 한 개만 존재하는 것은 아니다

만약 weight가 없는 graph에서 sssp를 해주려면
각각의 edge가 모두 동일하게 1의 weight를
갖고있다고 가정해주면 된다

s가 출발점이기 때문에
s에서 s로 가는 거리는 0으로 설정해준다
그런 다음 s에서 갈 수 있는 노드는
t와 y이고 모두 weight가 1이니
t와 y 노드에 1을 설정해준다
그리고 위 그림에서 t.π, y.π가 있는데
이 것은 해당 노드까지 도달하기위해
이전에 거친 노드를 저장해주는 것이다
그 다음 x와 z에 대해서도 동일하게 설정해주고
x.π, z.π도 동일하게 설정해준다
사실 unweighted graph에 대해 sssp를 해주고싶다면
단순하게 BFS를 이용하면 된다

weighted graph에서는 BFS가 잘 작동을 하지 않는다
위 예시만 봐도 s에서 t까지 한 번에 가는 것은 10인데
s->y->t로 가는 경우는 총 weight의 합이 2기 때문이다
Dijkstra's Algorithm

따라서 weighted, directed graph에서
sssp를 찾는 알고리즘은 Dijkstra's Algorithm으로
문제를 해결 할 수 있다
그리고 다익스트라는 모든 weight가
음수가 아니라는 것을 전제로 두고 있다

다익스트라 알고리즘으로 위 그래프의
sssp를 풀어보자
s에서 s로 가는 것은 일단 0이기 때문에
s를 0으로 초기화를 해준 뒤
t, y, x, z는 무한대로 초기화를 해준다
그런 다음 s에서 갈 수 있는 t와 y에
각각 더해지는 weight값을 설정해준다
이러한 과정을 relax라고 한다
따라서 t에는 10을 relax해주고
y에는 5를 relax해준 다음
각 node의 π값도 s로 세팅해준다
그 다음 t와 y 중에서는 y가 더 작은 값이니
y를 선택해준 다음
다시 y에서 뻗어나갈 수 있는 노드를 거리 계산해준다
y에서부터 뻗어나갈 수 있는 노드는
t, x, z가 있는데 그 거리는 각각
t는 8, x는 14, z는 7이 된다
t까지의 경로도 s에서 바로 가는 것보다
y를 거치는 것이 총 거리 8로 더 작아지므로
t를 8로 업데이트해주고 t.π=y로 변경해준다
x와 z도 마찬가지로 거리를 relax해준다
그럼 남아있는(아직 파란색으로 칠해지지않은) 노드들 중에서
거리가 가장 작은 값인 z 노드를 선택한다

z에서 갈 수 있는 노드는 x뿐이기에
x를 13으로 relax를 해주고
x.π는 z로 설정해준다
그럼 남는 노드들의 총 거리는 8과 13이 되는데
이 중에서 가장 작은 8인 t 노드를 선택해준다
그러고 t에서 x로 가는 거리를 계산하면
9가 나오는데 기존에 있던 13보다 짧으니
x를 9로 업데이트해주고
x.π도 t로 변경해준다
이렇게 하면 알고리즘이 끝이나게되고
각각 node안에 있는 숫자가 실제 shortest path의 거리가 된다

다익스트라 알고리즘의 pseudo code이다
그래프 G가 주어지고, w는 weight, s는 source vertex이다
그리고 INITIALIZE-SINGLE-SOURCE에서
s를 제외하고 다른 노드들을 모두 무한대로 초기화한다
각 노드들의 π값들도 null로 초기화한다
그런 다음 s는 0으로 초기화한다
S는 확정된 path들의 집합이기에
처음에는 공집합으로 초기화해준다
Q는 남은 노드들 중 가장 짧은 노드를 찾기 위해한
minimum priority queue이다
그리고 Q에 모든 vertex들을 insert하면
값이 0인 s가 가장 위에 오게 될 것이다
그 다음 Q가 공집합이 될 때 까지 while문을 돌면서
현재 Q에 있는 애들 중 가장 distance가 낮은 node u를 뽑는다
u를 집합 S에 포함시키고
u에 인접한 이웃들을 한 개씩 돌면서 relax를 시켜준다
relax는 이전에 저장되어있던 값과
현재 값+weight를 비교해서 더 작은 값이 저장되도록 만들어주는 과정이다
그렇게 relax를 시켜주었으면
Q에서 해당 node는 제거해준다

time complexity에 대해 알아보자
initialize가 O(V), minimum priority queue에 넣는 것도 O(V)이다
while문을 V만큼 돌지만 decrease-key가
V만큼 일어나는 것은 아니고 총 edge의 개수만큼 발생한다
decrease-key는 한 번 수행할 때
O(log V)만큼이므로
while문의 총 time complexity는
O((V+E)log V)가 된다
따라서 위 값이 총 time complexity가 된다

다익스트라 알고리즘의 증명이다
증명법에는 여러 가지가 있으나
induction을 사용하여 증명하는 방식을 가져왔다
우선 델타(s, v)라는 notation을 정의하는데
이는 s에서 v까지 가는 가장 짧은 거리를 뜻한다
따라서 우리가 증명해야 할 것은
v의 거리 d가
델타(s, v)와 동일하다는 것을
증명하면 된다
우선 증명을 하기 전에 Base Case를 세팅하면
S가 공집합인 상황은 알고리즘을 시작하자마자 이므로
당연히 v.d = 델타(s, v)는 true가 된다
또, S에 1개가 들어오는 순간 이 node는 source vertex가 되므로
v.d = 0, 델타(s, s)=0이 되므로 동일하기에 true가 된다

집합 S안에 여러 개가 들어있다고 가정해보자
또, minimum priority queue에서 한 개를 뽑았는데 걔가 u라고 가정해보자
그리고 그걸 S에 포함시킨다
우리가 보여야하는 것은 u가 뽑힐 때 갖고 있는 d의 값이
실제 s에서 u로 가는 최단 distance라는 것을 보여줘야한다
따라서 이것을 증명하기 위해서 몇 가지를 세팅해주겠다
우선, vertex y라는 개념을 세팅하는데, 이는
shortest path가 있다고 가정을 할 때에
shortest path 상에서 아직 S에 들어있지 않지만
바로 첫 번째로 맞닥뜨릴 vertex이다
vertex x는 y직전에 등장하는 파이로
집합 S안에 속해있는 vertex이다
그럼 이제 5번째 항목에 있는 부등식을 증명해보자
우선 델타(s,y) = s에서 y까지의 실제 최단거리는
델타(s,u) = s에서 u까지의 실제 최단거리보다 같거나 작다
이는 y는 u까지 가기 위해 거쳐야하는 vertex이기 때문에
당연히 y까지의 최단거리는 u까지의 최단거리보다
작거나 같을 수 밖에 없다
그 다음 부등식을 보면
s에서 u까지 가는 최단거리는
u의 distance보다 작거나 같다고 하는데
이도 당연하다
델타(s, u)는 실제 최단거리이기 때문이다
그 다음 부등식에서는 u의 distance값이
y의 distance값보다 작거나 같다고하는데
이게 성립하는 이유를 생각해보자
u는 minimum priority queue에서 뽑은 것이기 때문에
S에 포함되지 않은 vertex들 중에서 가장 distance가
작은 vertex가 된다
따라서 u.d <= y.d는 성립하는 부등식이 된다
따라서 결국은 우리가 증명해야할 것은
s에서 u까지의 실제 최단거리와
u.d가 동일하다는 것을 보여야하는 것이고
이를 s에서 y까지의 최단거리가
y.d와 동일하다는 것을 증명하는 방식으로 증명하려한다

위를 증명하기 위해 lemma를 한 가지 도입했다
shortest path는 경로가 여러 개일 수가 있는데
그 여러 개의 경로 모두 다 가장 짧은 path라는 것이
lemma이다
그래프 G에 대해서 p = <v0, v1, ... , vk>는
v0에서부터 vk까지 가장 짧은 path라고 가정한다
그러면 pij는 i에서부터 j까지 도달하기 위한
p의 subpath가 되고
p가 shortest path이므로 pij또한 i에서 j까지
도달하는 shortest path가 된다
왜 pij가 shortest path가 될 수 밖에 없는지 증명해보자
만약 pij가 가장 짧은 path가 아니라고 하면
pij 이외에 더 짧은 path가 있는 것이다
그래서 그 더 짧은 거리를 p'ij라고 하면
위의 p가 가장 짧은 path가 되는 것에 모순이 생기기 때문에
pij가 가장 짧은 path가 될 수 밖에 없는 것이다

그래서 다시 원래 증명으로 돌아가서
델타(s, y) = y.d가 동일하다는 것을 증명해보자
y가 현재 들고있는 d의 값은 x의 값이 w(x, y)를 더한 값보다
작거나 같은 것은 당연하다
왜냐하면 x가 이미 집합 S안에 들어가있다는 것은
이미 한 번 탐색이 되었다는 뜻인데
그 때 분명이 x에서 y로 가는 edge도 탐색이 되었을 것이다
그 이후에 y.d값이 다른 vertex들을 통해서
relax가 되었을 수 있지만
relax 로직 상 distance값이 더 작아질 수는 있어도 커질 수는 없다
x.d = w(x, y) = 델타(s, x) + w(x, y)가 나오는데
이전의 inductive hypothesis에서 델타(s, x)값과 x.d값이
이미 동일하다는 것을 증명했기 때문에
이 또한 당연히 성립하는 등식이 된다
또한, 위에서 세팅해주었던 lemma를 통해서
델타(s, x) + w(x, y)는
델타(s, y)와 동일하다는 것이 도출이 되는데
shortest path안에 있는 subpath들도
모두 shortest path가 되고
이에 따라 당연히 델타(s, x)도 shortest path가 되고
델타(s, x) + w(x, y)의 값은 델타(s, y)와 동일해진다
따라서 위 증명에 의해서
델타(s, y) <= y.d의 부등식이 성립하게 되는데
y.d가 사실 실제 최단거리보다 작아질 수는 없다
따라서 이걸 부등식으로 작성하면
y.d >= 델타(s, y)가 되는데
델타(s, y) <= y.d와
y.d >= 델타(s, y)를
모두 만족시키려면 결국
y.d = 델타(s, y)밖에 없게 된다
따라서 y.d = 델타(s, y)가 성립하게 된다

그렇다면 저번 시간에 배웠던
Minimum Spanning Tree(MST)와
Shortest Path Tree의 차이점은 무엇일까?
MST의 정의는 모든 graph들의 vertex를 연결하는 tree인데
모든 weight들을 합한 값이 최소가 되는 tree를 말한다
MST와 SPT는 의미적으로 공통점이 많지만 다르다
MST가 source에서 vertex로 돌아가는데
최소로 돌아간다는 보장이 없다
두 가지의 pesudo code를 살펴보며 차이점을 봐보자

다익스트라 알고리즘을 공부하면서 느꼈을 수도 있겠지만
다익스트라는 앞의 MST찾기 알고리즘에서 배웠던
Prim's Algorithm과 매우 유사하다
다익스트라와 prims의 결정적인 차이는
vertex 값을 어떻게 업데이트시켜주냐이다
다익스트라는 relax 방식으로 업데이트를 시켜주는데
relax는 현재 vertex까지 도달한 최단거리에다가
edge의 weight값을 더한 값을 update해준다
하지만 Prim's Algorithm은 현재 vertex까지 도달한
최단거리는 고려하지 않고
그냥 주변 candidates에서 가장 짧은 값만 고려한다

다익스트라는 weight가 음수일 때 사용할 수 없다
기본적으로 다익스트라는 greedy algorithm이기 때문에
weight가 줄어든다는 가정이 없다
이러한 negative weight를 해결하기 위한 방법이
다음 시간에 배울 Bellman-Ford 알고리즘..
그럼 다익스트라에 대한 내용은 여기까지-!
'강의 > computer science' 카테고리의 다른 글
| [computer science] all-pair shortest paths(1) (APSP) (0) | 2024.12.01 |
|---|---|
| [computer science] single-source shortest path(2), Bellman-Ford Algorithm(벨만포드 알고리즘) (1) | 2024.11.29 |
| [computer science] Dynamic Programming (동적 프로그래밍) (0) | 2024.11.20 |
| [computer science] Red-Black Tree (1) | 2024.11.18 |
| [computer science] Graph, Tree, Minimum Spanning Tree(Prim's, Kruskal's Algorithm) (0) | 2024.11.11 |