본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간에는 neural network를 어떻게 fitting 시키는지에 대해서 배워보자
이번 시간에는 기본적인 gradient descent에 대해서
다음시간에는 back propagation에 대해서 배운다

우리가 training을 하려면 데이터가 있어야하고
이걸 바탕으로 loss function이 있어야한다
이번 교재에서는 데이터의 개수를 I라고 표기하는데
이걸 가지고 우리가 어떤 함수의 파라미터인 phi를 조절하는 것이다
그래서 이때의 loss를 계산하라면 3개가 필요한데
파라미터, 모델, 데이터이다
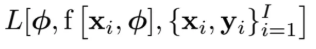
위를 바탕으로 loss를 계산하면 그게 train loss가 되는 것이다
우리가 통상적으로는 이 loss를 phi에 대한 함수로 아래와 같이 쓴다

모델이나 데이터에 대한 표기는 생략한 것이다
위는 우리가 다른 파라미터를 주면 다른 scalar값을 내뱉는 어떤 함수이다

우리가 모델을 학습을 한다는 것
즉 fitting을 시킨다는 것은
이 loss를 minimize하는 phi hat을 찾겠다는 뜻이다

그렇다면 우리가 학기 초반에 배웠던 linear regression을 바탕으로
한 번 설명해보자
위 ppt의 linear regression에서 기울기가 phi1, 절편이 phi0이 된다
저 2개가 define되면서 어떤 선이 되는지가 정해지는 것이다
loss는 위 선을 어떻게 fit 시키냐에 따라서 달라진다
위에서는 Loss가 7.11이 나왔는데
여기서 이 Loss만 보고서 얘가 큰지 작은지는 알 수가 없다

우리가 이전에 배운 linear regression은 closed form solution으로
데이터를 한 번에 구할 수가 있었다
하지만 이번에는 그게 아니고 어떻게 이 linear regression이
iteratively하게 fit되는지를 살펴보자
왼쪽 contour의 x가 intercept, y가 slope이라
왼쪽의 점은 parameter space에서의 점이다
linear regression에서는 loss function이 convex함수이다
따라서 2D에서의 covex이기 때문에 위와 같은 contour를 갖고
어두우면 어두울수록 loss가 낮은 것이다
contour의 등고선 line은 loss가 같은
서로 다른 linear function들의 모임이다

자 위에서 0에서 1로 이걸 update했다고 해보자
아직 어떻게 update시켰는지는 설명하지 않았다
아무튼 loss가 낮아지는 방향으로 파라미터를 조절해서 update를 시켰다
오른쪽 b 그래프에서 모델이 loss가 줄어드는 쪽으로 바뀐 것을 확인할 수 있다

그렇게 계속해서 네번째까지 쭉쭉 update를 했다고 해보자
4번이 가장 loss를 minimize하는 선이 된다
사실 이 과정이 gradient descent인데
아직 구체적으로 어떻게 하는지는 설명하지 않았다
아무튼 이렇게 최소가 되는 부분이 어딘지 찾으면서
순차적으로 파라미터를 조절해나가며 update하는 과정이다
linear regression은 closed form이 있어서 이렇게 굳이 할 필요가 없지만
그냥 이렇게 gradient descent로 차근차근 구할 수도 있다는 것이고
위 linear regression같은 경우는 loss가 무조건 convex 함수라고 했다
이 convex 함수에서는 local minimum이 무조건 global minimum이 되기 때문에
linear regression에서는 무조건 gradient descent를 써도 수렴한다

자 아주 잠깐 고등학교에서 배운
2차함수 미분을 살펴보자
위 2차함수 식을 미분하면 저렇게 된다는건 다들 알고있을 것이다

그럼 위 2차함수의 꼭짓점에서 미분하면
미분값이 0이 된다

그럼 오른쪽의 점에서 미분하면? 미분값은 2인 양의 값이 나온다
그럼 만약에 내가 미분값이 2인 오른쪽 점에서
미분값이 0인 점으로 가고싶으면 어느 방향으로 가야할까?
미분 방향으로 가야할까? 미분의 반대방향으로 가야할까?
미분의 반대방향으로 가야한다

그럼 x가 4일 때는? 미분값도 4이다
이때도 미분값이 작아지는 지점을 찾으려면
여전히 미분의 반대 방향으로 가야할 것이다
그런데 내가 좀 더 빨리 꼭짓점으로 가고싶다면
미분값이 4인 지점에서는 step을 크게 밟는 것이 좋을 것이다

반대쪽도 마찬가지이다
반대쪽에서도 얘가 미분의 반대방향으로 가야지만 최소점으로 갈 수 있다
참고로 선형함수에서의 mean square error가 convex이기 때문에
local minimum = global minimum이 되는 것이다
deep neural network에서는 절대 이렇지 않다
비선형함수면 loss function이 mean square error더라도
전체 파라미터 기준으로는 convex함수가 되지 않는다

이제부터 gradient descent를 살펴보자
파라미터가 N+1개가 있다
우리는 Loss를 미분을 하는데 이때 phi를 기준으로 미분을 구한다
그런데 phi는 벡터값이기 때문에 각각의 element-wise하게 partially 미분하면된다
그럼 내가 이 loss의 미분식을 바탕으로 phi들을 update 하고싶다
어떤 방향으로 해야할까?
미분값의 마이너스 방향이다

위 식에서 알파는 양의 상수이다
보통 step size 혹은 learning rate라고 불리는데
내가 step을 어떻게 할지를 결정하는 양의 상수이다
이렇게 되면 위식은 항상 미분의 반대방향으로 step을 걷게된다
따라서 이렇게 파라미터를 update해주는 것이 바로 gradient descent이다
여기서 매우 중요한 것은 여기서 말하는 Loss라고 하는 값은
모든 데이터포인트의 개수를 기준으로 하는 것이다
즉, 모든 데이터의 loss를 가져와서 하는 것이다
모든 데이터를 다 들어간 것에 대한 미분값을 말한다

그렇다면 다시 아까 linear regression에서 살펴보자
Li는 i번째 데이터포인트에서 얻은 loss이다
아까 위에서의 loss는 전체 데이터에서의 summation이라고 했다
그럼 이 때의 미분값을 구해보자

L이라는 함수에 대해서 미분값을 구한다는 얘기는
Li의 summation에 대해서 미분값을 구한다는 뜻이다
미분은 sum 안쪽으로 들어갈 수 있기 때문에
각각의 포인트들에서 미분한 것을 다 더해주는 것과 결과가 같다

이렇게 각 Phi들을 기준으로 element-wise하게 미분해주면된다

phi0 방향으로 미분한 방향이 위 슬라이드 contour에서
점의 왼쪽 화살표이다
phi을 기준으로 미분한건 위 화살표 방향이다
그래서 이 2개를 합성하면 저 대각선 방향이 된다
이 loss를 minimize하려면 미분의 반대방향으로 가야한다고 했다

그래서 왼쪽 대각선의 반대방향인 오른쪽 아래 방향으로 가게 된 것이다

그래서 첫 번째 update는 이렇게 0에서 1로 되었다
처음의 선은 눈으로 봐도 fit이 안좋았는데
1번 선은 0에 비해선 얼추 좋아진 것을 확인할 수 있다
그럼 여기서 끝나나? 그건 당연히 아니다
1이라는 점에서 또 더 fit하도록 update 해줘야한다

또 각각의 element 기준으로 미분값을 구한뒤 방향을 찾는다
그런 다음 미분의 반대방향으로 update를 시켜준다

이런 과정을 한번 두번 세번 계속해서 반복하다보면
결국 loss가 최소가 되는 점이 나오게 된다
위 슬라이드에서는 4번이 loss가 최소가 되는 구간이다

loss를 3차원으로 보여주면 b처럼 된다
우리가 아까 봤듯이 파라미터가 업데이트되면서 선들이 어떻게 update 됐는지 알 수 있다

아까 linear regression에서의 loss function은 무조건 convex함수라고 말했다
여기서 convex 함수의 정의를 잠깐 짚고 넘ㅇ너가보자
convex 함수의 정의는 임의의 두 점에서 선을 그렸을 때
그 선이 항상 그 함수 위에 있는 함수를 얘기한다
그렇다면 non-convex 함수의 정의는 함수에서 임의의 두 점에서 선을 그었을 때
그 선이 함수 아래에 있을 "수"도 있는 것이다
항상 아래에 있는 것은 아니다
convex를 뒤집은 것이 concave함수이고
그럼 concave함수의 정의가 어떤 임의의 두 선을 그으면
무조건 그 함수 밑에 있는 함수가 된다
concave에서나 maximum을 찾는 문제나
convex에서 minimum을 찾는 문제는 동일한 문제이기 때문에
concave나 convex를 모두 퉁쳐서 convex 함수 문제로 얘기한다
아무튼 그렇다면 loss function이 convex함수가 아닐때의 단점이 뭐냐?
2개의 점으로 선을 그었는데 그 선이 함수의 밑이 될 수도 있다는 것
즉, local minimum이 global이 아닐 수 있다는 것
local minimum이 여러개 존재할 수 있다는 것이다
saddle point도 존재할 수 있다
아무튼 미분값이 0인 것만 찾다가는 최소가 아닌 지점에서 머무르게 될 수 있다는 것이다
그래서 optimization이 어려워지게된다

그렇다면 non-convex 함수의 optimization이 얼마나 어려운지 한 번 보자
위의 Gabor model이라는 함수가 있다
input은 그냥 1차원이라고 하자
파라미터가 2개있고 이게 phi0, phi1이다
이렇게 생긴 함수가 있는데 이걸 어떻게 optimize 할 수가 있을까

true model은 모르고 데이터는 이렇게 있다고 하자
우리의 Job은 최대한 저 데이터를 잘 fit하는 phi0, phi1을 찾는 것이다

위 함수로 contour를 그리면 이렇게 생겼다고 한다
아까 Linear랑은 완전히 다른 모습을 볼 수 있다
저 등고선들이 있고 점으로 찍힌 부분들이 다 Local minimum이다
지금 이 함수를 보고 복잡하다고 생각할 수 있는데
neural network는 이것보다 훨씬 더 복잡하다
참고로 이 데이터를 기준으로 했을 때
그래프 C가 global minimum인데
다른 local minimum들이 얼마나 많이 존재하는지 알 수 있을 것이다

이게 실제로 gradient descent를 수행한 것이다
여기서 1과 3의 출발점은 global minimum에 수렴한 것을 알 수 있다
하지만 2번에서 출발한 것은 local minimum으로 빠진 것을 알 수 있다
그럼 이걸 어떻게 해결하면 좋을까

stochastic gradient descent라는 것이 있다
이 stochastic gradient descent의 펀치 라인은
gradient descent에서 Noise를 추가하는 것이다
여기서 stochastic은 확률적이라는 뜻인데 이 메커니즘이 뭐냐면
앞에서 gradient를 구할 때 가지고 있는 모든 데이터를 기준으로 gradient step을 밟는다고 했는데
stochastic은 데이터 1개를 기준으로 한다
다시 말해서 데이터 100개가 있으면 100개의 데이터 중에서
1개만 uniformly random으로 sample한다
눈감고 주사위를 굴린 다음에 3이 나왔다?
그럼 그냥 3번 데이터포인트 기준으로 gradient를 구하고 step을 밟는 것이다
그 다음에 또 random sample을 하는 것이다
즉, stochastic gradient descent는 데이터포인트 1개만가지고 gradient descent를 밟는 것이고
minibatch와 착각을 많이 하는데
minibatch는 여러 개의 sample로 batch를 하는 것이다
mini batch와 stochastic은 엄연히 다르다
stochastic gradient descent는 정의상 1개의 데이터를 뜻한다
그럼 데이터를 어찌됐던 한 번 step 밟을 때 데이터를 다 쓰는게 아니니까
sample을 해서 한 번 다 스윽 돌았을 때
데이터를 다 한 번씩 썼을 때
그걸 1 epoch이라고 한다

여기서 딥러닝 모델을 코드로 돌려본 사람이 있다면
아마 practice에서는 SGD를 사용할 때
데이터 100개가 있으면 그냥 shuffle 한 다음 한번에 쫙 sweep한다
그리고 그걸 1 epoch이라고 한다
원래의 theory는 매번 randomly sample하는 것인데
실제 practice에서는 그냥 shuffle해서 순차적으로 수행한다
하지만 full batch GD는 모든 데이터포인트에서
gradient step을 밟는 것이다
minibatch는 batch를 전체 데이터에서 sample하고
거기에서만 gradient step을 밟는다

그렇다면 그냥 full gradient descent랑 SGD의 차이를 한 번 살펴보자
왼쪽에서는 2에서 출발하면 local minimum에 빠지게 된다
이 경우에서 "그냥 좀 운이 안좋은거 아닌가?"
"다시 해보면 2도 global로 빠질 수 있지 않나요?"라고 물어보는 경우가 있는데
그렇지 않다
full gradient descent에서는 100번을 다시 repeat해도 그대로이다
달라질게 하나도 없다
그런데 오른쪽에 있는 SGD에서는 똑같은 점 2에서 출발한 경우를 보자
global minimum으로 수렴하는 것을 볼 수 있다
1번도 마찬가지
그리고 이 SGD는 step들이 상당히 지그재그한 것을 볼 수 있다
왜 그럴까?
앞에서 SGD의 펀치라인은 noise를 넣는 것이라고 했다
이게 noise를 넣었기 때문에 full gradient descent와는 다르게
SGD에서는 같은 initial point로 시작해도 그 결과가 달라질 수가 있다
그럼 이렇게 하는 것에 장점이 뭐가 있을까?
noisy한게 장점일까?
절대 그렇지 않다 random한 것은 장점이 아니다
위 Ppt slided에서 두번째 그래프를 잘 살펴보자
왼쪽의 full gradient descent에서는 100번 돌려도
2번째 initial point에서는 global minimum으로 가지 못한다
하지만 오른쪽은 조금 noisy하더라도 갈 수 있게 된다
그게 바로 SGD의 가장 큰 강점이 되는 것이다
그렇다면 SGD로 했을 때 절대 Local minimum에 안빠진다는 보장이 있나?
그런 보장은 없다
그래도 full gradient descent처럼 무조건 Local minimum으로 빠지는 경우는 피할 수 있다는 것이다

한마디로 SGD의 가장 큰 강점은
local minimum에서 빠져나올 수 있는 여지가 있다는 것이다
반면에 full gradient descent는 무조건 local minimum에 빠지게 된다
그렇다면 우리가 만약 Mini batch로 SGD를 구하려고 한다면
데이터가 100개면 100개 기준으로 다 미분해야한다
이렇게 되면 전체 데이터에 대한 loss를 계산해서 더한 다음
이거에 대한 minimum을 찾는 full gradient descent보다
per step당 계산량은 적어진다
그렇지만 항상 좋은 solution을 찾는다는 것은 아니다
그리고 또 한가지 중요한 것은
SGD가 full gradient descent에 비해 계산 속도가 빠르다?
절대 그렇지 않다고 한다
per step당 계산량이 적은 것은 사실이다
하지만 per step당 계산량이 적다고 해서
수렴속도가 더 빠른 것은 절대 아니다
https://fa.bianp.net/teaching/2018/eecs227at/gradient_descent.html
\star + - = \alpha \lambda \beta R \alpha= \beta= \beta = 0 \beta=1 \alpha = 1/\lambda_i \text{model} 0 p_1 0 \bar{p}_1 2\sqrt{\beta} \lambda_i \lambda_i = 0 \alpha > 1/\lambda_i \max\{|\sigma_1|,|\sigma_2|\} > 1 x_i^k - x_i^* \xi_i \beta = (1 - \sqrt{\alp
fa.bianp.net
위 url에 접속하면 gradient descent에 대해서 설명이 잘 되어있다
저기서 여러 example들을 테스트 해볼 수가 있다
그리고 SGD에 대한 것도 example들을 볼 수 있다
위에서 full gradient descent랑 SGD랑 비교해보면
SGD가 더 수렴이 빠른게 절대 아님을 알 수 있다
nice한 convex함수라면 그냥 gradient descent를 하는 것이 훨씬 낫다
SGD는 상당히 Noisy하기 때문이다
다시한 번 정리하자면 SGD가 full보다 per step 계산량이 적은 것은 사실이지만
수렴 속도가 더 빠른 것은 절대 아니다
noisy하기 때문이다
그렇다면 이런 noise를 쓰는 이유는
SGD를 사용하면 local minimum에 안빠지게해줄 수 있기 때문이다
그리고 loss함수에서 그냥 절댓값 minimize 해도되는데 굳이 제곱해서 하는건
그냥 수학적으로 더 큰값을 minimize하는것이 좋기도 하고
미분하기 위함이다

이제 여기서 좀 더 optimize를 잘해보려는 논력을 해보자
SGD를 하던 full batch를 하던
우리가 어떻게 gradient를 구했다고 해보자
그런데 우리가 gradient로 간다는 것은
경사를 따라서 내려가는 일인데
우리가 등산했다가 하산하는 상황을 생각해보자
매번 step을 바꾸면서 하산하는게 아니고
이전에 내려오던 방향으로 계속해서 내려오게된다
momentum은 따라서 이전에 내가 내려오던 방향이나 gradient를 축적해놓은 다음
그 방향대로 그대로 가는 것을 말한다
m이 모멘텀인데
첫번째 iteration의 m1은 아무것도 없을테니 그냥 gradient descent를 받게되고
이전의 m이 있다면 이전의 경사를 기억하고
그걸 반영해서 경사를 조절하게 된다

위 식에서 베타는 새로 계산된 gradient와
지금까지 가지고있던 momentum을 smoothing하는 역할을 해준다
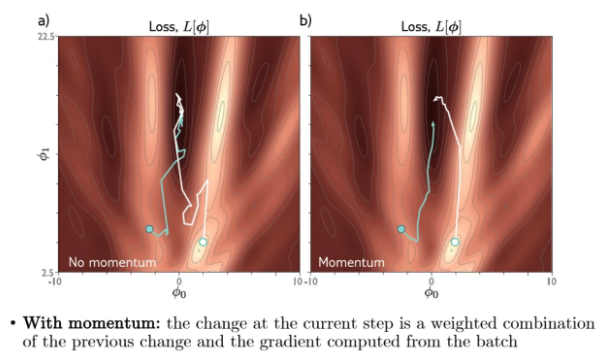
그렇다면 momentum을 활용한 SGD를 한 번 살펴보자
오른쪽이 momentum을 적용한 결과인데 조금 더 smooth하다는 것을 알 수 있다
그래서 이렇게 global minimum으로 noise를 줄이고 갈 수 있는 것이다
SGD의 단점이 매 step마다 지그재그하고 noisy한 것들이었는데
그것들을 좀 더 smooth해지게 만든 것이다

Nesterov monemtum에 대해서 그럼 알아보자
결국 모멘텀은 앞으로 어디로 갈지에 대한걸 예측하는 것과 굉장히 비슷하다
그래서 nesterov momentum은 내가 어느쪽으로 가는게
더 loss를 줄일 수 있을지도 정하는 것이다
위 ppt에서 왼쪽이 그냥 momentum 방향인데
오른쪽의 Nesterov를 보면 더 빠르게 global minimum 방향으로 향한걸 알 수 있다

이제 Adam에 대해서 알아보자
그냥 gradient descent를 했을 때는 step size를 적당히하면 smooth하게 잘 된다
그런데 똑같은 convex 함수라도 step size가 크면 오른쪽처럼 될 수가 있다
하지만 이 step size는 절대적인 값이 아니기 때문에
우리가 이정도면 크고 이정도면 작다라는게 사전에 알기가 힘들다

그렇기 떄문에 우리가 해주는 것은 우선 gradient를 normalize를 한다
gradient지만 gradient를 축적해놓은게 momentum이기 때문에
이를 momentum이라고 부르겠다
normalize를 위해서 모멘텀을 제곱한걸 square root 한 다음 분모에 둔다
우리가 관심있는건 방향이 아니라 크기이기때문에 제곱을 한다
그런데 쟤가 너무너무너무 작아서 0에 가까울 수도 있고
아니면 아예 0일수도 있기 때문에 아주 작은 양수인 입실론값을 더해준다
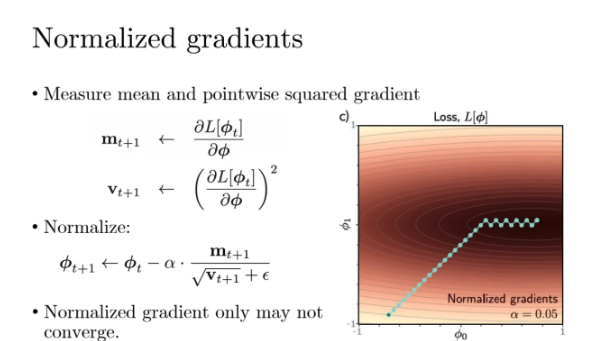
이렇게 gradient를 normalize를 시키면
gradient가 굉장히 unit한 step을 밟게 된다

그렇다면 Adam은 무엇을 하는 애이냐?
이렇게 normalize를 시켜서 너무 경사가 가파르고 변동이 심한 step은 좀 줄여줘서
step에 의해서 너무 sensitive하게 바뀌는 것을 방지해주는 것이다

위의 그냥 normalized gradients랑 Adam을 비교해보자
Adam이 각광을 받는 이유는 non-convex 함수에서
local minimum을 잘 빠져나가면서
그나마 global minimum에 가깝게 잘 optimize가 되기 때문이다
하지만 요즘은 실제로 Adam을 능가하는 optimization 알고리즘이 나왔다고 한다
SGD는 50년전에 나왔고 Adam은 10년 전에 나왔는데
실제로 논문에서도 가장 널리쓰이는 조합은 SGD + Adam이라고 한다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Regularization (Dropout, Early Stopping, Transfer Learning, Data Augmentation) (1) | 2025.11.11 |
|---|---|
| [DL] Computing Gradients (Forward Pass, Back Propagation) (0) | 2025.11.10 |
| [DL] Deep Neural Networks (0) | 2025.11.02 |
| [DL] Shallow Neural Network (0) | 2025.10.29 |
| [ML] Clustering (k-means clustering, hierarchical clustering) (0) | 2025.10.27 |