본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

오늘은 딥러닝에서 사용할 수 있는 regularization에 대해서 배웠다

참고로 우리가 이전에 linear regression에서 ridge와 lasso를 배웠는데
그때도 이 방법론들이 linear regression에만 국한된 것은 아니라고 했었다
일단 우리가 이 regularization을 왜 하는지부터 좀 생각을 해보자
우리가 이전시간부터 계속 말했는데
왜 training data에서 학습을 열심히 시켰는데 test data에서 성능이 안나올까?라고 한다면
첫 번째는 train data에 너무 overfit한 나머지 test에서 일반화가 안되는 경우가 있다
이전에도 말했지만 overfitting과 data shift는 아예 다른 얘기이다
overfitting의 정확한 정의는 train과 test data의 분포는 같음에도 불구하고
train의 노이즈마저 fit을 시키는 것을 말한다
아무튼 결론적으로 regularization이라는 개념을 한 마디로 정의를 하기는 어려운데
쉽게 설명하자면
내가 현재 train data만 가지고 거기에 잘 맞게 fit을 시켜서
에러를 최소화시켰는데 이걸 살짝 믿지않겠다는 것이다
train data에 대해서 가장 least square로 에러를 최소화하는 어떤 점을
나는 믿지않겠다는 뜻이다
아무튼 이렇게 정규화라는 것을 정의하기는 어려운데
한 마디로 일반화를 더욱 잘시키기 위한 것이 목적이다
주어진 데이터만 믿고 estimate하는 것을 살짝 피하고
내가 가지고 있는 어떤 preference나 knowledge를 추가하겠다는 것이다
그리고 이걸 하는 ㅇ ㅣ유는 일반화를 잘 시키기 위함이다

regularization은 이렇게 다양한 방법들이 있다
이런것들을 다 통칭해서 regularization이라고 한다

우선 explicit하게 regularization을 하는 방법을 살펴보자
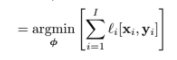
이게 우리가 알고있는 정규화하지않은 그냥 loss function이다

그런데 이 일반적인 그냥 loss function에서 내가 어떤 값을 더해서
이걸 minimize시키겠다는 것이다
g가 아직 무엇인지는 얘기를 안했는데
g가 어떤 양수를 띄는 함수라면 람다는 0보다 큰 값이 될 것이다

phi0, phi1이라는 파라미터가 있는 loss 함수가 있고 이게 non-convex라고 해보자
저 가운데 짙은 동그라미가 global minimum이고 나머지는 다 local minimum이다
왼쪽의 그냥 loss function에다가 regularization을 넣었다고 해보자
가운데가 regularization인데 이게 둥근 shape이 된다
여기서는 완전 circular한 모양인데 이게 geometrically하게 살펴보면
l2-norm과 유사한 형태라는 것을 알 수 있다
한 마디로 왼쪽의 non-convex loss함수에
l2-norm을 추가하게 되면
오른쪽 c가 나오게 된다
그리고 이렇게 원래 loss에서 regularization이 추가된 점은
기존 그대로가 아니고 살짝 달라지게 된다
location이 똑같지가 않은 것이다
하지만 우리는 regularization이 되기 전의 점은 믿지 않고
regularization이 수행된 이후의 c에서의 solution을 믿겠다는 것이다
그럼 c에서처럼 solution이 이동한 것을 뭐라고 말할 수 있을까?
bias가 생겼다고 말하라 수 있다
그럼 bias를 늘어나게해서 우리가 얻는 것은 무엇일까?
variance가 감소해서 Mean square error가 감소히길 바라는 것이다
그리고 regularization을 추가하면 함수가 smooth해진다
c를 보면 a에 비해서 많이 smooth한 것을 볼 수 있다
상대적으로 우리는 함수가 smooth해지는 것을 선호한다는 것이다

이걸 우리가 likelihood 관점에서 바라보자
현재 우리가 주어진 데이터가 있고 파라미터들을 가지고 likelihood를 최대화해보자
logistic regression 할 때 우리가
어떤 데이터가 있을 때 저걸 현재 데이터에 대한 likelihood를 maximize하는 문제로 바라볼 수 있다고했다
그래서 이제

이걸 maximize하는 phi를 찾고싶은 것이다
이걸 찾기 위해서는 대부분의 경우 log를 씌워서 곱을 sum으로 만들어서 하는게 더 쉽다
그럼 여기서 regularization을 추가한다는 것은 뭐와 같나?
위 식에 사전확률인 prior를 추가한다는 것과 같다
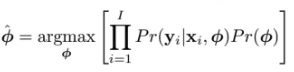
우리가 사전확률을 집어넣는다는 것은
이 파라미터들이 이런 분포에서 왔으면 좋겠다는 것을 집어넣는 것과 같다

우리가 앞에서 위에서는 이렇게 페널티를 집어넣어줬는데
이걸 probabilistic한 관점에서는 위와 같이 prior를 집어넣는다

즉 이렇게 두 식이 mapping이 될 수 있는 것이다
위에서 log prior에 마이너스가 붙은 이유는
위 식은 argmin인데 아래 식은 argmax이기 때문에
log앞에 마이너스를 붙인 것이다
한 마디로 l2-norm을 하고싶다고 얘기하는 것은
거기에 상응하는 prior를 추가하는 것과 동일한 것이다

가장 대중적으로 많이 쓰이는 것은 l2-norm을 추가한 l2 regularization이다
각각의 파라미터 term들을 제곱한 다음에 이걸 summation해주고
람다가 앞에서 control해주는 역할을 한다
우리가 linear regression 할 때 이걸 배웠는데
거기에만 국한된건 아니고 neural network에 적용해도된다
꼭 neural network가 아니어도 상관없다
아무튼 이 l2 penalty를 위 식에다가 집어넣는다는 것은
우리가 쟤를 둥근 ball shape 안에다가 집어넣는다는 뜻이다
이렇게 한다는 것은 우리는 상대적으로 비슷한 크기의 loss를 원하는데
그 phi size가 작았으면 좋겠다는 것이다
그래서 우리가 이걸 다른 발로 weight decay라고도 부른다
phi의 size를 shrinkage한다는 뜻이다
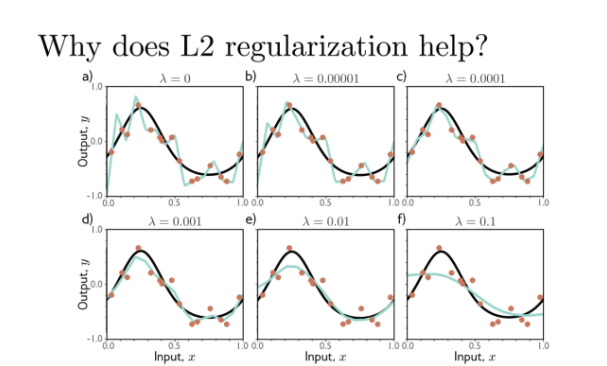
우리가 linear regression에서 l2 regularization을 넣은 것은
각각의 베타값들, 즉 기울기가 크지 않았으면 좋겠다는 것이었다
그렇다면 Neural network에서는?
제일 왼쪽 a는 람다가 0인 그냥 바닐라 모델이다
검정색 실선이 실제 true model인데 우리가 실제로는 이걸 알 수 없다
검정색 true model과 함께 비교하는것이 아니고 초록색 함수만 가지고 비교할 수 있다
위의 각 오렌지 점들이 data이다
l2 penalty를 넣은 다음 람다를 이용해서 조금씩 컨트롤 하는 것이다
람다가 증가하면 wiggly했던 함수가 조금씩 더 smooth해진다
완전히 매끄러워진다기보다는 wiggly하던 것이 사라진다는 의미이다
각각의 Piece wise region에서의 기울기가 너무 크지 않기를 바란다는 것이다
만약 람다가 너무 세다면 모든 weight들이 다 0에 비슷해지면서 굉장히 flat한 함수가 될 것이다
그래서 적절한 사이즈의 페널티를 찾는 것이 중요하다
그렇다면 이 적절한 람다는 어떻게 구할 수 있을까?
바로 cross validation으로 구할 수 있다
또한 착각하면 안되는게 이 함수들이 매끈하다고 해서 piecewise 함수가 아닌 것은 아니다
각각의 region에서는 여전히 piecewise 함수이다

이제 implicit regularization에 대해 배워보자
우리가 보통 Neural network를 학습시키면서 l2 penalty를 넣을까?
넣는 경우도 있는데 안넣는 사람들도 꽤 많다
그런데 이걸 넣지않아도 생각보다 학습이 잘된다
linear regression을 할 때는 l2 penalty를 넣지않으면 상당히 불안해지는데
neural network는 보통 L2 penalty를 굳이 넣지 않아도 잘될 때가 있다
무조건 잘된다는 것이 아니고
넣지 않아도 생각보다 잘 될 때가 있다
왜그렇게 될까?

non-convex 문제에서는 local minimum이
무조건 global minimum이 아니라는 것에서 문제가 발생한다
그런데 이게 SGD나 GD나 상대적으로 더 선호하는 path가 존재한다

왜 explicit한 정규화를 넣어도 잘 안되는 경우가 있을까
이건 직관적으로 한 번 살펴보자
왼쪽이 full batch GD이다
저 짙은 파란색 실선이 gradient descent를 continuous하게 찾아가는 것이다
오른쪽의 좀 더 밝은 하늘색은 우리가 하는 것처럼 step size로 가면서 정답을 찾아가는 것이다
왼쪽처럼 이걸 연속적으로 수행했을 때가 사실
가장 natural하게 정답을 찾을 수 있는 golden standard라고 할 수 있다
참고로 위 경우는 저 위쪽의 선이 다 global minimum이라서
저 선 안에만 있으면 다 최소화가 된 것이라고한다
아무튼 원래의 golden standard는 왼쪽처럼 continuous하게 하는 것인데
이렇게하면 너무 작업이 많아지기때문에
우리가 step size로 approximate하는 것이다
그런데 여기서 c를 보자
이 친구의 loss에다가 b라는 정규화를 추가한 다음 실제로 full optimization을 수행해보면
c와 같이 살짝 오른쪽으로 tilted 된 것을 확인할 수 있다
즉, 우리가 a에서 정규화를 넣지 않고 step size로 approximate를 한 것과
c에서 정규화를 넣어서 continuous하게 수행한 것이 동일한 path를 갖는다는 것이다

위 설명을 읽으면 더욱 이해가 쉬울 것이다

그렇다면 왜 이런 현상이 일어나게 되는걸까?
이 부분은 너무 자세하기 알려고하지말고 그냥 참고만 해도 된다고 한다
원래 loss에다가 l2 정규화를 추가하면
gradient에서 그냥 걷는것과 동일해진다고 한다
이러한 현상은 SGD에서도 마찬가지로 발생하는데
애체오 loss term에다가 뭔가 페널티를 넣은 것이 아닌데
optimization 과정에서 자연스럽게 penalty를 넣은 것과 동일한 경로로 가게 된다는 것이다

여기서 a랑 b랑을 비교해보면 비슷해보이지만 살짝 smooth해지는 경향이 있다
그럼 regularization이 있는게 surface를 좀 더 smooth하게 만드는 것이다
smooth해지면 optimization을 찾기가 좀 더 쉬울 수가 있다
adam도 결국 마찬가지로 적용된다

지금부터는 neural network를 학습하는데에 있어서
여러가지 trick들을 좀 알아보자

Early stopping은 train data로 neural network를 학습하면서
loss들을 쭈욱 줄여가는 방식으로 학습한다
그런데 neural network같은 경우는 파라미터 숫자가
전체 데이터포인트의 숫자보다 많은 경우가 대부분이다
그렇다보니 사실상 파라미터들이 모든 데이터포인트들을 기억할 수도 있는 것이다
그렇게 되면 진짜 overfitting이라는 문제가 발생하는 것이다
그래서 우리가 neural network를 학습할 때 파라미터들을 순차적으로 학습시키기 때문에
뒤로갈수록 각각의 데이터포인트들의 noise까지 학습시킬 가능성이 높다
따라서 어느정도 학습을 시키다가 도중에 학습을 멈춰버리는 것이 early stopping이다

얘네들은 train loss이다
제일 오른쪽이 가장 wiggly한 함수인 것을 확인할 수 있다
계속해서 학습이 진행될수록 train error는 줄겠지만
일정수준 학습을 하고 도중에 멈춘다면 true함수를 더 잘 대변할 수도 있는 것이다
그렇다면 우리가 언제 학습을 멈추는게 좋냐?
이건 우리가 cross validation을 이용해서 찾아내야한다
그래서 우리가 실제로 딥러닝 학습을 시킬 떄
중간중간 iteration별로 validation error를 찍어보는 것이다
중간의 train error와 validation error를 보면서
train loss는 낮아졌는데 validation loss가 커진다면
그 시점에서 학습을 멈춰야하는 것이다

앙상블을 이제 살펴보자
한 개의 모델이 아니고 여러 개의 모델을 보는 것을 앙상블이라고한다
우리가 이걸 tree based해서 했었는데 neural network에서도 해도된다
모델 10개가 있으면 10개에 대해서 각각 prediction을 한 다음 걔네의 평균을 이용하면 된다
그럼 classification을 할 때는 어떻게 하면 될까?
방법은 여러가지가 있는데 voting으로 해도 되고
softmax 사용 전에 logit값에서의 평균을 하던지 하면 된다
그렇다면 10개의 모델들은 어떻게 만들까?
나에게 train data가 있고 내가 이걸 가지고 neural network를 10개를 만들고싶다고 해보자
똑같은 train data를 사용하면 안되는데, 그럼 이걸 어떻게할까?
앞에서 배웠던 bootstrap으로 가능하다
bootstrap으로 train data를 가지고 10개의 copy를 만들수있다
걔네들의 copy를 만든다는 말은 origin data와 완전히 같지는 않지만
같은 분포에서 오는 데이터셋들을 만들 수 있다는 말이다
그래서 그걸로 10개의 bootstrap 데이터를 만든 뒤
각각의 bootstrap 데이터에 대해서 각각의 neural network를 학습시키면 모델이 10개가 나오는 것이다
그게 바로 bagging인 것이다
사실 위 bootstrap을 사용하는 방법 말고도 아주 쉽게 여러 모델을 만드는 트릭이 있다
이건 neural network가 좀 특별해서 가능한 것인데
만약에 우리가 neural network 모델을 10개를 만든다고 가정해보자
그럼 neural network는 non-convex이기 때문에 initial point가 어디냐에 따라
수렴하는 위치가 달라질 수 있다
그래서 각각 10개의 initial point들을 다 다르게 한 다음에 모델을 학습시키면
10개의 네트워크 모두 파라미터 space에서 starting point가 다른 모델이 나오게 된다
얘네가 생각보다 같은 곳으로 수렴하지 않고 다른 곳으로 수렴한다
그래서 궁극적으로 서로 다른 10개의 neural network를 갖게 된 것이다

아무튼 bootstrap을 쓰던 initial point를 다르게 하건 여러개의 모델을 만들면 된다
위 예제는 bootstrap으로 다른 neural network를 만든 예제이다
original dataset을 가지고 만든 것이고
얘를 bootstrap으로 해서 각각 4개의 데이터셋을 만들었다
위에서 데이터포인트의 크기가 뭐냐면
bootstrap은 origin data가 들어갈 떄 여러번 들어갈 수 있기 때문에
그 frequency를 크기로 나타낸 것이다
우리가 이렇게만 눈으로 봤을 떄는
model1이 orignial보다 좋냐 나쁘냐를 판단하기는 힘들다
하지만 우리에게는 4개의 서로 다른 모델이 있기 때문에
이를 average하는 방식으로 앙상블을 수행하면 된다
이 앙상블 된 함수가 original의 회색 모델보다 더 smooth한 것을 볼 수 있다
앙상블도 여전히 모델을 smooth하게 만들어주는 효과가 있기 때문다
앙상블하는 모델의 개수가 더 많아질수록 더 smooth한 함수가 될 것이다

다음으로는 dropout을 살펴보자
네트워크를 train 할 때 a가 full network이다
이 dropout들은 문자 그대로 일부 hidden unit들을 꺼버리는 것을 의미한다
걔네들은 그냥 학습할 때 0으로 만들어버리는 것이다
그런 다음 나머지 꺼지지않은 애들을 이용해서 학습하는 것이다
그런데 이제 이 어떤 hidden unit을 꺼버릴지를
randomly 선택하는 것이다
이걸 매 iteration에서 수행하게 된다
다른 iteration이면 다른 hidden unit들이 drop out되게 된다
위 예제는 2개만 drop out 되도록 했는데
실제로는 상당히 많은 hidden unit들이 deactivate된다
그리고 이 dropout은 train 될 때만 수행하는 것이고
inference 단계에서는 모든 hidden unit을 사용한다

그럼 이 dropout이 어떤 효과를 만드냐?
만약에 a와 같은 original 함수가 있다고 치자
이 친구에서 어떤 hidden unit 8번을 끄니까 위와같이 b처럼 솟구치게된다
그럼 이상태로 내가 만약 8번 unit을 끈 상태에서 계속해서 네트워크를 업데이트하라고 하면
저 솟구친애가 결국 c와 같이 밑으로 내려오게 된다고 한다
이렇게 저 삐쭉삐쭉한 kink한 것들이 없어지게 된다고 한다
그렇다면 결국 이 dropout도 무엇을 하는 것이냐?
wiggly한 함수를 smooth하게 만드는 것이다
unit 기준으로 꺼진다는 것은 결국
piece wise region이 사라진다는 뜻이다
지금까지 우리가 배운 대부분의 trick들은 전부
함수를 덜 wiggly한 함수로 만드는 것이다
그리고 앞에서도 말했지만 학습에는 drop out을 적용해도
inference할 떄는 모든 unit을 다 사용해야한다
그리고 혹시 특정 테크닉을 하는데에 있어서 forward pass를 할 때 drop out을 하는 테크닉도 있는데
여기서 이 얘기를 하는 것은 아니라고 한다
혼동할 수 있어서 굳이 설명은 안하겠다

사실 이 dropout이라고 하는 것은 학습할 때 노이즈를 집어넣는 것과 비슷하다
weight에다가 randomly하게 선택해서 집어넣는것과 비슷하다
그런데 이런 Noise를 집어넣는 테크닉은 또 있다
내가 input 데이터에다가도 살짝 살짝 이걸 흔들면서 학습을 할 수 있다
어떤 Numeric한 value라고 한다면 이걸 그대로 학습하는게 아니고
noise를 넣으면서 학습할 수가 있는 것이다
b, c로 갈수록 input에다가 noise를 집어넣었더니 애들이 smooth해지는 것을 확인할 수 있다
또 그렇다고 noise를 너무 많이 넣으면 너무 smooth해지기 때문에
적절한 noise를 집어넣어서 적절한 complexity를 갖도록 해야한다
input에다가 noise를 집어 넣을 수 있다는 말은
y에다가도 noise를 집어넣을 수 있다는 말이 된다
y가 흔들리면서 train이 되었다는 소리는 학습됐던 weight들도 흔들리면서 결국 같은 효과를 낸다
너무 noise를 많이집어넣으면 말도 안되는 함수가 나올 수도 있다
그래서 우리가 지금까지 본 테크닉들은 모두 일단 적절히 하는게 중요하다
그럼 그 적절한 정도의 regularization을 어떻게찾냐?
기승전 cross validation이다
아무튼 직관적으로는 우리는 이러한 기법을 사용해서
함수들을 다 smooth하게 만들 수 있다는 말이다

이젠 베이지안 관점에서 한 번 살펴보자
앞에서부터 계속해서 설명했지만 결국 이러한 테크닉들이 다 뭔가?
너무 wiggly하지 않고 적절한 smooth한 함수로 만들어서
너무 overfit하지 않도록 만들고싶다는 것이다
그럼 이걸 베이지안의 관점에서는 어떻게되나
결국 베이지안의 관점에서는 어떠한 것도 fix되는 것은 없다
우리가 가지고 있는 이 phi라는 애들도 결국은 다 확률적인 것이다
그래서 베이지안에서 구하고자 하는 것은 phi들의 분포이다
이런 phi들의 분포를 만드는 식이

위와 같은 것이다
위 식에서 사전확률 prior는 우리가 데이터를 보기 전에
각각의 파라미터들이 어느 분포에서 왔는지에 대한 변수이고
앞의 파이는 Likelihood 값이다
밑 분모의 적분은 모든 phi에 대해서 다 예측을 시킨다음
그 분포를 가중평균낸 값이다

따라서 이러한 관점에서 모델을 바라보면
결국 다 그냥 확률적인 값이 된다
여기서 시그마 phi라는 애는 prior분포의 분산이다
이게 상대적으로 크다는 것은 우리가 가지고있는 사전지식(prior)이 그렇게 세지 않다는 뜻이다
그렇게 된다면 당연히 함수가 wiggly해질 것이다
여기서 prior의 분산이 작아진다는 뜻은
가지고 있는 확률이 상당히 특정방향으로 강해진다는 뜻이고
우리가 가지고있는 사전 지식을 더 세게 넣는다는 뜻이다
따라서 그렇게 되면 덜 wiggly한 함수가 나오게 되는 것이다
우리가 처음에 additive한 penalty를 넣는것은 확률에서 prior를 넣는것과 비슷하다고했다
그래서 분산을 적게 준건 l2 penalty를 더 크게 준것과 마찬가지인 것이다

그런데 우리는 애초에 우리가 구하고자하는 저 posterior 분포를 알아내기가 힘들다
prior는 어떻게든 집어넣을 수 있지만
posterior를 계산하는 것은 현재 가지고있는 기술로는 불가능하다고 한다
특히 neural network에서는 더더욱 불가능하다고한다
그래서 현존하는 대부분의 연구에서는 approximately하게 구한다
각각의 weight에 대해서 exactly하게 분포 계산은 불가능하기때문에
approximate하게 샘플하거나 분포를 그나마 근사할 수 있는 방법들이
더욱 최근에 나오고 있다
잘 이해가 안간다면 예시를 들어보자
내가 지금 neural network 모델을 만들려고 하는데
삼성전자의 주식이 얼만큼 상승할 것인지 예측하는 neural network를 만든다고하자
그럼 내가 만약에 내가 만든 모델이 어떤 input을 넣자
output으로 12만원이라고 냈다고 치자
그럼 얘는 그냥 point estimate가 된다
12만원이라는 output을 내는 point estimate가 된다
하지만 우리는 여기에 확률적인 것을 넣고싶은 것이다
예를 들면 95%의 확률로 12만 5700원이됩니다와 같은 것을 넣고싶은 것이다
그럼 우리는 삼성전자의 분포를 알 수 있는 것이다
이 분포를 그런데 우리가 아까 봤던 앙상블로도 수행할 수 있다
만약 10개의 모델이 있다고 치자
그럼 저 삼성전자 주가에 대한 모델의 예측값은 10개가 나오게 되는 것이다
그럼 걔네를 approximate해서 사용할 수 있는 것이다
걔네를 가지고 신뢰구간도 말할 수 있다
모델이 많으면 많을수록 더 우리의 신뢰구간은 accurate해지게된다
SWAG와 같이 SGD로 optimize를 할 때 좀 더 확률적으로 해서
마치 분포처럼 움직이게하는 그런 애들도 있는데
아무튼 이런 테크닉들이 많고
최근에도 계속해서 활발하게 연구되고 있는 방향이라고 한다
교수님께서 생각하시기에 꽤나 중요한 방식이라고 하신다 ㅠ

지금까지 우리가 배운건 주어진 데이터에 대해서
좀 더 smooth한 모델을 만드는 것이었다
페널티를 집어넣듯, 확률적으로 바라보든 어떻게 됐던지 간에
주어진 데이터만 가지고 fully error만 최소화하는 것이 아니고
regularization을 통해서 일반화를 하고싶다는 것이었다

거기서 조금 더 나아가서 내가 어떤 task를 가지고
다른 모델이나 다른 task로 가져와서 학습을 좀 더 용이하게 만들 수 있을까 하는 것이다
위 예시에서 어떤 task가 이미지를 가지고 각각의 object들을 segment하는것이라고 하자
그걸 구분하는 segment 모델이 존재한다
image to image 모델인 것이다
이 segment 모델은 학습이 되었다고 하자
이제 그냥 segment가 아니고 depth를 하려고 하면
위에서 학습된 segment 모델을 아주 유용하게 사용할 수 있는 것이다
이렇게 기존에 학습된 어떤 애를 가지고
내가 다른 모델을 학습시키는 것을 transfer learning이라고 한다
multi-task learning은 동시에 모델을 학습하면서
같은 input에서 동시에 segment와 depth 예측을 하는 것을 말한다
서로서로 모델을 공유하면 서로 학습하는데에 있어서 도움이 된다
마지막으로 self-supervised learning은
부분적으로 어떤 path를 마스킹한 다음 예측을 수행하는 것을 말한다
이러한 기법들은 가지고 있는 prediction을 좀 더 improve하는 방식이다

마지막으로 data augmentation을 살펴보고 오늘 수업 정리를 마쳐보려고한다
이건 되게 널리 쓰이는 방식인데
이미지가 1개 있는데 이걸 살짝 tilt하거나 rotate하거나
색을 바꾼더거나 blur를 넣는다거나 하는 방식으로
오리지널 데이터 1개를 가지고 여러 개의 데이터를 만들어서
학습에 도움이 되게끔 하는 테크닉을 말한다

우리가 지금까지 배워본 방식들을 정리한 것이다
어떤 것들은 explict하게 어떤 것들을 implict하게 수행하였고
아니면 데이터만 가져와서 학습을 더 용이하게 하는 경우도 있었다
하지만 결국 이러한 regularization의 목적은
generalization을 잘하기 위함이다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Convolutional Neural Networks (CNN) (0) | 2025.11.17 |
|---|---|
| [DL] Computing Gradients (Forward Pass, Back Propagation) (0) | 2025.11.10 |
| [DL] Fitting Models (0) | 2025.11.05 |
| [DL] Deep Neural Networks (0) | 2025.11.02 |
| [DL] Shallow Neural Network (0) | 2025.10.29 |