본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

이번 시간부터는 이제 neural network의 다양한 활용에 대해 알아본다
그 첫번째는 바로 Convolution Neural Network
일명 CNN이다

이 CNN은 이미지에 아주 널리 쓰이는 테크닉인데
우리가 이미지를 neural network의 input으로 받는다
그렇게 되면 image가 neural network의 input으로 들어오면서
숫자 혹은 pixel value로 들어가게 된다
색상값이 RGB이기 때문에 내가 어떤 색상 이미지를 받으면
채널별로 RGB컬러가 있고 채널별로 pixel value가 존재한다
이런 값이 input으로 들어가게 되서 아웃풋으로는
image를 classificatin 할 수 있는 각각의 class값이 나와야한다
class가 100개가 있따고 하면 그 100개의 class에 대한 각각의 확률값들이
위 ppt slide처럼 벡터 형태로 output으로 나오게 된다
그렇게 계산한 결과 왼쪽 사진은 가장 높은 확률로
bicycle class에 속한다는 결과가 나오게 되는것이다

이건 CNN으로 할 수 있는 또다른 예제이다
이미지를 input으로 줬을 때 이 이미지 안에 어떠한 object가 있고
그게 무엇인지를 찾는 task도 수행할 수 있다

그 다음으로 또 CNN에서 할 수 있는 것은
이미지가 있을 때 그 이미지를 어떻게 segmentation할 것인지이다

이제 본격적으로 CNN이라는 모델이 어떻게 작동하는지를 살펴보자
input이 예를 들어서 224 * 244 사이즈라는 아주 작은 사이즈라고 해보자
이는 이미지 중에서 아주 작은 사이즈임에도 불구하고
RGB 컬러가 이 사진에 있게되면 input dimension만 15만 정도가 나온다
그렇다면 우리가 이걸 fully connected neural network에 넣으면
1 hidden layer만 하더라도 22빌리언 정도의 weight가 나오게 된다
그런데 이렇게 어마어마하게 많은 수의 weight들을 사용해서 우리가 얻는 장점이 큰가?
한 마디로 결국 이미지를 각각의 픽셀 별로 weight를 더한다는 것인데
이미지를 모든 픽셀에 대해서 다 학습한다고 해서 크게 나아지는게 있나?
내가 설령 computation이 너무 좋은 컴퓨터를 갖고있어서 그 계산이 가능하다고해도
이미지같은 경우는 근처에 있는 픽셀들은 상당히 값이 비슷하기 때문에
각 픽셀별로 모두 weight를 더하는 것이 비효율적일 수 있다
이미지는 주변 픽셀들과 correlated 될 가능성이 매우 높은데
우리가 이걸 fully connected로 하면 그걸 걍 다 독립적으로 학습하는 것이 된다

따라서 이미지를 이용한 학습에는 이런 불편함이 있었고
이걸 좀 더 어떻게 하면 효율적으로 학습할 수 있을까?에서 시작한 것이다
convolution network는 이미지를 patch로 바라본다
이미지 전체에서 공유할 수 있는 재사용하는 parameter를 사용한다고 하는데
좀 더 자세하게 알아보자

이제 본격적으로 CNN을 배우기 전에 개념들에 대해서 좀 알아보자
함수가 invariance하다는 것은
오리지널 input이 x인데 x에다가 함수를 보내서 나오는 output과
x에다가 transformation을 살짝 한 다음에 이걸 f 함수에 넣은 경우
이 output들이 같은 경우 x는 t에 대해서 invariance하다고 한다

invariance example에 대해서 보자
이 이미지에 대해서 classify 한다고 하자
오른쪽 그림은 왼쪽 그림을 살짝 shift 한 것이라고 한다
그런데 이를 classification을 하면 왼쪽이든 오른쪽이든
여전히 눈이 덮힌 산으로 classification을 하게 된다
그렇다면 이 경우는 shift라는 Transformation을 수행해도
classification이라는 함수 f에 넣은 결과는 동일해지기 때문에
이런걸 invariance하다고 말하게 된다
심지어 좌우를 flip한다고 해도 classification에서는 동일하게
눈이 덮힌 산으로 분류를 할 것이다
이런게 invariance이다

그렇다면 Equivariance도 한 번 살펴보자
equivariance는 x를 tranformation해서 f에 넣늑너랑
x를 f에 넣은 다음 transformation하는 것이 동일하다는 것이다
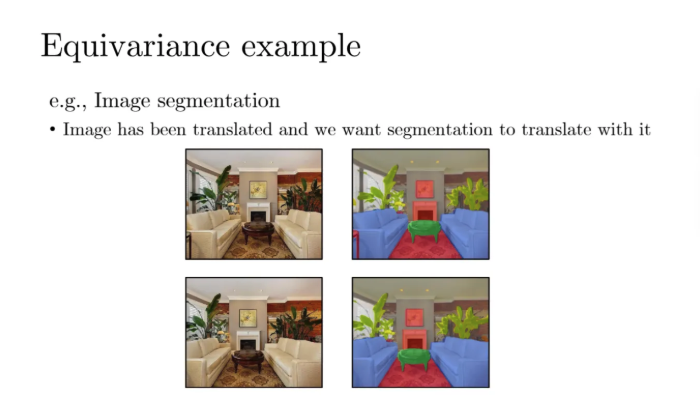
Equivariance의 예시를 한 번 살펴보자
이미지 segmentation같은 경우
내가 이 친구들의 Input을 가지고 shift 한 다음 segment를 하든
이 친구들을 segment를 한 다음에 shift를 하든 결과는 동일하다는 것이다
이렇게 task의 특성상 이런 특성들을 고려해서
우리가 어떠한 아키텍처 모델을 생각할 수 있을까라는 것이다

우선 convolution을 가장 쉽게 알아보기 위해서 1D에서 어떻게 하는지부터 보자
input이 1D라는 것이 아니고
2D인 이미지를 1D의 벡터로 일렬로 세웠을 때를 말하는 것이다
위 ppt slide에서 x는 벡터이고 벡터의 dimension이 weight인데
우리가 우선 디멘션이 3인 어떤 커널을 가지고 이 x를 훑어본다고하자
x라는 Input의 length가 100이라고하면 (dimension이 100인게 아님)
얘보다 length가 더 작은 커널을 가지고 움직이면서 연산을 수행한다
위 예시에서는 커널 사이즈가 3인걸 예시로 들었는데
반드시 3일 필요는 없다

이런식으로 3개짜리 커널로 input 벡터를 훑고 가보자
i가 2라고 하면 i번째를 기준으로 -1과 +1한게 훑어진다
그런 다음 양 옆에 있는 weight들이 sum이 다음 z가 된다
지금은 커널사이즈가 3이기 때문에 오메가는 3디멘션이 된다
위 그림처럼 이렇게 커널이 훑고지나가면서 weighted sum한 것이
다음 레이어에 전파되는 형식이다

그리고 위와 같은 특징은 아까 우리가 봤던 equivariant한 성질을 가진다고한다
이게 왜 정확하게 equivariant한지 이해가 잘 안되어서 gpt에게 물어보았다

답변을 보니 이해가 좀 되었다
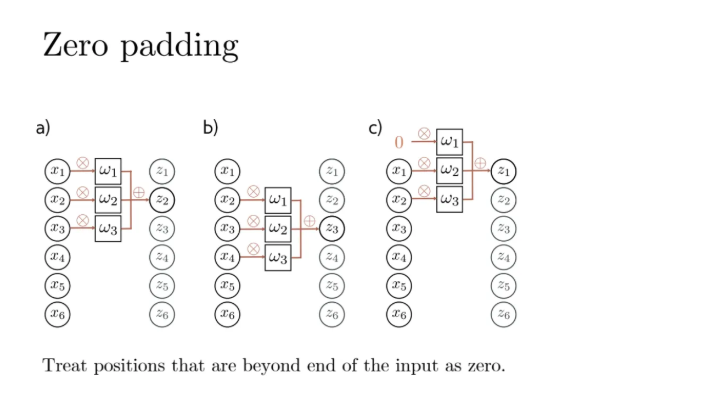
그렇다면 우리가 이렇게 input vector를 기준으로 커널로 훑는데
그렇다면 x1에서는 위의 element가 없는데 어떻게 할까?
그럼 그냥 x1보다 위의 값은 0이라고 치고 계산할 수가 있다
이걸 zero padding이라고 한다

zero padding 말고 다른 방법도 있다
오메가 기준으로 내가 곱해줄 수 있는 것부터 시작하는 것이다
이렇게 되면 다음 레이어의 unit 개수가 달라지게 될 것이다
이렇게 zero padding을 쓰든지 아니면 다른 방식을 쓰든지는
우리가 선택할 수 있는 것이다
커널 사이즈도 우리가 선택할 수 있다
위 예시는 3이지만, 이걸 4나 5로 우리가 바꿀 수도 있다

convolution network를 수행할 때 우리가 specify해줘야되는 것들이 있다
그 종류에는 stride, kernel size, dilated 등이 있는데 뒤에서 더 볼테지만 간단히 말해보자면
우리가 위 예시에서는 모든 vector를 커널로 하나하나 다 훑었지만
실제로 반드시 그럴 필요는 없다
그걸 조절하는 것이 stride이다
그리고 커널 사이즈는 앞에서도 계속 나왔지만
커널이 사이즈가 5라고 하면 파라미터도 5개가 되는 것이다
커널 사이즈가 3이라고 하면 파라미터 개수도 3개가 되는 것이다
즉 커널 사이즈는 내가 갖고있는 파라미터의 개수가 된다
마지막으로 dilated는 중간중간에 필터들이 어떻게 성기게 만드는지인데
이건 뒤에서 그림을 보면서 더 자세히 알아보도록 하자
그리고 아까 말했듯이 패딩을 어떻게 하는지
제로패딩을 할 것인지 그것도 선택할 수 있다

a를 한 번 살펴보자
a에서 커널 사이즈는 3이다
그런데 내가 제로패딩을 넣어서 시작해서 커널로 훑을때
바로 그 다음 x1부터 시작하는게 아니고
stride가 2이기 때문에 한 칸 건너 뛰어서 x2부터 시작하게된다
이렇게 되면 그 다음 레이어는 4개의 unit만 생기게 된다
stride가 만약에 1이었다고하면 우리가 앞에서 봤던것처럼
그냥 순차적으로 진행하는 것이되고
다음 레이어인 z unit의 개수는 8개가 되었을 것이다
그렇다면 이제 c를 한 번 살펴보자
stride는 1인데 커널사이즈가 5이다
그리고 이전 벡터의 unit개수와 다음 레이어의 unit 개수가 동일하므로
zero padding을 사용했다는 것을 알 수 있다
통상적으로 커널의 개수는 센터점이 잡히는 홀수개로 설정한다
d에서 dilation이 2이라고 했는데 지금 이게 보면
필터가 딱 붙어있는게 아니라
한 번에 2칸씩 건너뛰면서 weighted sum을 하는 것을 볼 수 있다
중간중간에 빼먹는 unit들이 존재한다
하지만 결과적으로 이전 레이어를 커널이 한 번 훑으면서
모든 x들을 훑기는 한다
그렇다면 여전히 각각의 네트워크 수에서 파라미터 숫자는 커널 사이즈로 정해진다
걔를 가지고 내가 stride는 얼마나 띄엄띄엄 갈건지 정하는 것이고
dilation은 내가 필터를 얼마나 성기게 할 것인지를 정하는 것이다
여기서 우리가 중요하게 봐야할 key는
x의 크기가 엄청 크건 말건
우리의 네트워크에서 파라미터 숫자는 달라지지 않는다
이미지 사이즈가 달라진다고해서 파라미터 숫자가 달라지는게 아니고
커널 수는 똑같은데 다음 레이어의 유닛 숫자가 많아지는 것이다
파라미터의 숫자는 그냥 똑같은 것이다

그럼 우리가 지금까지 배운 convolution에 있는 요소들을 넣은
convolution layer들을 수식으로 나타내보자
convolution network를 수식으로 나타내면
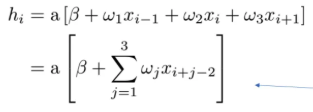
지금 위 식은 이전 레이어에서는 xi가 있었던 것이고
커널 사이즈가 3인 것이 된다
이전 i-1과 i+1이 위 식처럼 weighted sum이 되고 intercept까지 추가해서
위 식처럼 나타나는 것이다
이 식은 convolution network에서의 unit 1개가 되고
a는 activation이 된다
그럼 밑의 식은 무엇이냐?
fully connected network에서는 i번째 hidden unit을 보면
걔네들은 전체 input에서 다 와서 모아서 activation을 수행한 것이다
D는 전체 input 사이즈이고
그래서 fully connected network는 첫번째 레이어만 보더라도
input dimension에 의해서 파라미터 개수가 dependent한데
convolution layer는 그렇지 않다는 점이 가장 큰 차이점이다

그럼 convolution network가 구조상 어떻게 되는지 살펴보자
a가 fully connected layer인데
결국 이걸 b와 같은 matrix로 나타낼 수 있다
각각의 connection matrix로 나타낼 수가 있고
높은 value가 더 어두운색, 낮은 value가 더 밝은색을 갖는다
6*6이기 때문에 fully connedted라서 파라미터 숫자는 36개가 가득차야한다
그런데 c의 convolution의 경우를 살펴보자
convolution은 사실 주변에 있는 애들만 연결된 것이다
커널사이즈가 3개면 h2를 기준으로 x1, x2, x3이 weighted sum을 한 것이고
이런식으로 쭉쭉 내려가게 된다
matrix에서 하얀색으로 된 것은 그냥 0이다
또 옆의 b matrix에서는 각각 다 unique한 값을 띄는데
d는 row wise로 값들이 같은 것을 볼 수 있다
파라미터가 3개밖에 없기 때문이다
이렇게 훨씬 더 적은 숫자로 이미지에 있는 정보를 표현할 수 있는 것이다
그렇다면 e도 한 번 잘 살펴보자
여전히 convolution size는 3인데
숫자가 더 적어진 것을 볼 수 있다
이는 stride가 2로 되었기 때문이다
따라서 한 개씩 순차적으로 내려가면서 계산해준게 아니고
두 개씩 순차적으로 내려가면서 계산한 것을 볼 수 있다
그렇다면 왜 stride를 사용할까?
파라미터 숫자를 줄이기 위함이 아니다
계산을 더 줄이기 위함이다
물론 이렇게 하면 정보의 손실은 반드시 발생한다
그래서 stride를 무조건 크게한다고 좋은게 아니다

그렇다면 이제 channel에 대해서 알아보자
convolution은 network가 input을 받았을 때
커널 기준으로 weighted average를 수행하는 것이다
그러고나서 ReLU activation이든 뭐든 activation을 수행해준다
그래서 information이 손실이 된다
그래서 이런 정보의 손실을 방지하기 위해 하나의 필터가 아닌 여러 개의 필터를 사용한다
이게 바로 채널이다

위 예시를 한 번 잘 살펴보자
첫 번째 필터는 오메가 1, 2, 3이다
이렇게 오메가 1,2, 3으로 이루어진 커널로 한 번 훑으면
다음 레이어에서 첫번째 줄인 h1부터 h6까지가 나오게 된다
그 다음에는 오메가 4, 5, 6으로 이루어진 두 번째 필터로 또 다시 훑는다
그렇게 두번째 필터로 계산된건 두번째 레이어에서 h7부터 h12까지가 된다
만약 우리가 세번째 필터도 적용하고 싶다면 다음 레이어에 세번째 줄이 생기게 될 것이다
참고로 필터별로 커널 사이즈는 다 다를 수가 있고
2개의 커널로 훑고지나가기 때문에 output channel은 2개가 된다

input channel이 여러 개이고 output channel이 1개인 경우 그럼 어떻게 할까?
내 커널이 그냥 두겹인거라고 생각하면 편하다
이 친구들을 위 slide처럼 각각 element wise로 곱해서 더해주면
저렇게 다음 레이어의 결과값이 나오게 된다

임의의 input channel, 임의의 output channel에 대해서 위와 같이 만들 수 있다
weight matrix가 오메가가 된다
지난 시간에는 레이어 사이의 오메가는
앞단의 레이어와 뒷단의 레이어로 정해지는 matrix였는데
convolution에서는 그렇지가 않다
dimension은 input channel과 거기의 kernel size로 결정된다
그런데 만약에 ouptut channel이 1개가 아니고 여러개라고 한다면
input channel 개수와 output channel 개수와 kernel size가 존재하는
Matrix가 아닌 텐서가 된다

왼쪽에서 kernel size는 3이니까 3개만 들여다보게된다
input channel은 1개, output channel은 3개이다
위 그림에서 kernel size가 3개라서 오른쪽에 3개가 색칠된게 아니다
저건 그냥 channel 개수일 뿐이다

내가 여기서 hidden layer를 1개를 더 만들었다고하자
그리고 Output channel을 4개로 늘렸따
kernel size는 변경해도 상관없지만 우선 그대로 3으로 했다
그럼 오른쪽 두번째 hidden layer처럼 결과가 나오게된다
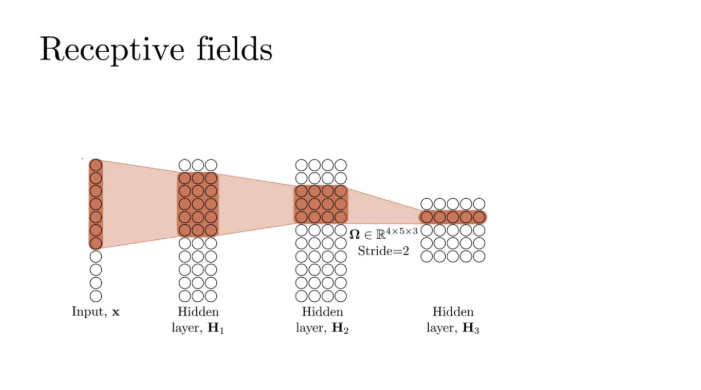
그다음 input channel은 4개이고 Ouptut channel은 5개로 했다
채널 개수가 반드시 늘어나야하는 것은 아니다
커널 사이즈도 중간에 충분히 바꿀 수 있지만 그냥 여전히 3개로 해준것이다
그런데 위 단계에서는 지금 3번째 레이어의 깊이가 확 준것을 볼 수 있다
이렇게 준 이유는 stride를 2로 해주었기 때문이다
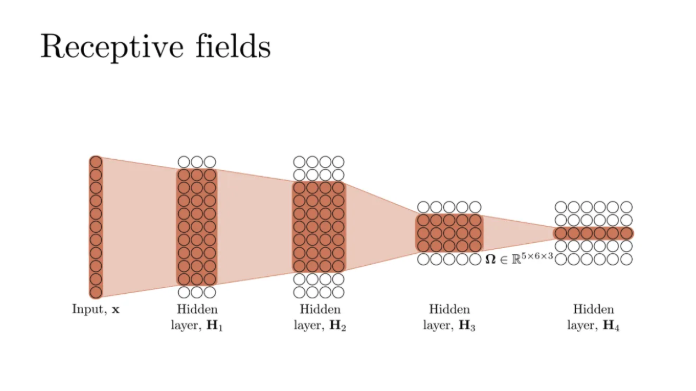
네번째 레이어로 갈 때는 input channel이 5개, output channel이 6개, kernel size가 3개이다
아까 맨 처음꺼 기준으로 저기에 영향을 미쳤던 input은 저만큼이 된다
각 unit들은 다 따로따로 activate되긴 한다
그런데 지금 벌써 4개의 레이어만 가도라도 6개의 숫자를 뽑아내는데
영향을 미치는 input layer는 전체가 되는 것을 알 수 있다
즉, 레이어를 쌓으면 쌓을수록 unit들의 row를 보면
input들에 상당한 영향을 미치고 있는 것이다

그렇다면 실제 데이터를 한 번 보자
원래 이게 뭐냐면 숫자 digit 데이터 셋이다
0123.. 뭐 이렇게 있는데 원래 이게 2 dimension 이미지인걸
각각의 숫자를 1D로 표현하기 위해서 그냥 선으로 폈다
그래서 숫자들을 그냥 1D로 표현하면 위 그림처럼 된다고 한다
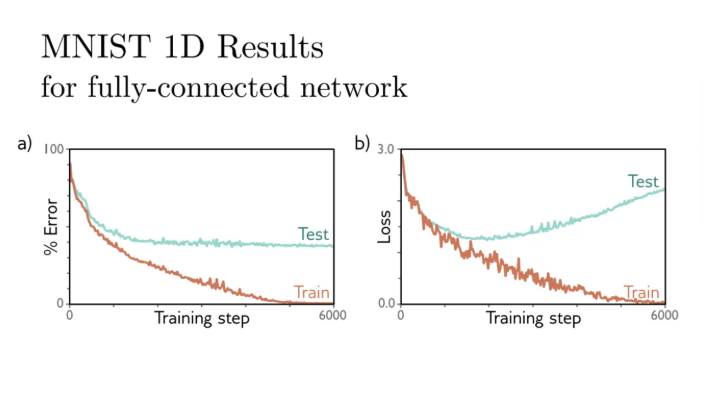
위 데이터를 fully connected network로 수행해봤더니
위 결과를 보면 train loss는 거의 0에 가깝게 수렴했는데 test loss는 어떤가?
성능이 매우 나쁜 것을 볼 수 있다
a와 b 모두 test에서의 성능이 매우 낮다

그렇다면 위의 똑같은 데이터를 convolution network에 넣어보자
hidden layer는 4개로하고, convolution layer는 그 중에서 3개
마지막 단에서는 fully connected layer를 사용하고
softmax로 확률계산을 통해 classification을 수행한다
gradient는 mini batch로 SGD로 수행한다

아까 그 2D 숫자 이미지를 1D로 표현했더니 Length가 40이 나왔다
이렇게 위 처럼 세 개의 convolution layer들이 있고
마지막에는 fully connected layer를 적용해준다
그런 다음 끝에 softmax로 학률계산을 수행해준다

같은 데이터셋으로 fully connected network로 수행한애와
convolution network로 수행한 애의 depth는 4개로 모두 동일했고
hidden unit의 개수도 모두 동일했다
fully connected layer를 했을 때 파라미터 개수는 15만개가 나왔는데
CNN으로 했을 때는 2050개밖에 나오지 않았다고 한다
그렇다면 이 두개 중에서 어떤 네트워크가 더 유연할까?

왼쪽이 CNN으로 수행한 결과이고 오른쪽이 fully connected network로 수행한 결과이다
train기준으로 b는 거의 너무 빠르게 0에 수렴한 것을 볼 수 있다
이건 fully connected network는 파라미터 숫자가 너무 많기 때문에 거의 외울 수 있기 때문이다
convolution neural network는 파라미터 숫자를 줄이는 것 뿐만 아니고
파라미터 숫자를 줄임에도 불구하고 Performance가 더 좋은 것을 확인할 수 있다
이는 이미지란 특성상 전체보다 local feature들이 더 중요한데
그냥 거기에 convolution network를 알맞게 만들었기 때문이다
이미지라는 학습 구조에 잘 맞게 만들어낸 것이 바로 CNN이다
CNN이 이미지에 대한 task를 잘 수행하는 이유는 파라미터 숫자가 적어서 좋은 것이 아니고
이미지라는 구조를 잘 활용하는 네트워크이기 때문에
파라미터숫자가 더 적음에도 불구하고 훨씬 효율적으로 수행할 수 있다는 것이다

그렇다면 CNN이 왜 이런 image 관련 Task를 잘 수행하나?
한 마디로 얘기하면 inductive bias이다
이미지라는 구조를 잘 활용한다는 것이다
이미지 뿐만이 아니고 내가 이러이러한 데이터가 있으면
이러한 데이터를 잘 살릴 수 있는 아키텍처를 잘 이용해야한다는 것이다

우리는 지금까지 1D convolution만 했는데
어차피 우리가 다루는 것은 2D image이기 때문에 이걸 한 번 살펴보자

아까 input이 그냥 벡터였을 때는 커널 3개를 훑으면 그냥 weighted sum이었다
그런데 Input이 2D가 되면 이건 그냥 matrix가 된다
그럼 만약에 input이 K*K matrix라고 하자
그럼 그 친구를 내가 가로 세로를 다 같이 바라보는 커널로
weighted sum을 해서 패스를 하게 되는 것이다
그렇게 되면 이제 input이 가로도 있고 세로도 있게 되니까
오메가의 index는 거기에 따라서 정해진다
그게 이제 다음 레이어의 i번째 j번째가 되는 것이다

3*3 커널은 위와 같이 한 개의 숫자로 만든다
좌측 상단부터 쫘아악 훑고 지나가는 것이다
zero padding이라고 하면 다음 레이어에서의 Hidden unit은 input size와 같아지게된다
zero padding이 아니라고 하면 Hidden unit은 잘려나가는 것이다

위 예시는 흑백이기 때문에 greyscale만 있으면 돼서 채널이 1개였다
하지만 컬러일 경우 RGB가 있어야 되기 때문에 Input의 채널은 3개가 된다
그럼 내가 kernel이 3이라면 3*3 커널이 되는 것이다
kernel size가 5면 5*5 커널이 되는 것이다
그래서 저 안에서 가져온 27개의 element에 대해서
element wise로 곱한 다음에 다 더하면
그 값이 딱 1개의 unit이 되는 것이다
따라서 output channel 1개를 만드는데에 저 weight tensor가 1개가 있어야한다
output channel을 2개 만들고 힢다면 저 weight tensor가 1개 더 있어야하는 것이다

이렇게 되면 이제 커널 사이즈가 K*K가 되는 것이다
나머지는 다 동일하다

이어서 CNN에서 사용하는 몇 가지 테크닉들을 살펴보자
만약에 내가 4*4 사이즈의 이미지가 있는데 이걸 2*2로 줄이고싶다고하자
그럼 이걸 어떻게 하면 될까?
우선 region을 만든 다음에
max pooling 혹은 mean pooling을 수행하면 된다
max pooling은 각 region에서 제일 큰 값만 뽑아오는 것인데
이렇게 하는 이유는 픽셀이 있으면 쟤네의 intense가 대부분 제일 크기 때문이다
mean pooling은 그냥 region에서의 평균값을 계산하는 것이다
위 과정은 그냥 차원을 줄이기 위해서 해 주는 것이다
weight를 곱해서 뭐 이런저런 계산을 하는 것이 아니기 때문에
그냥 우리가 원하는 사이즈 마음대로 줄이기 위함이다

그럼 반대로 우리가 원하는 사이즈로 늘릴 수도 있다
이걸 upsampling이라고 한다
각각의 레이어별로 사이즈가 항상 같을 수도 있고 다를 수도 있는데
이걸 맞춰주기 위해서 이런 과정을 수행하는 것이다

이런 upsampling은 transposed convolution으로도 수행할 수 있다
우리가 앞에서 배운 stride나 dilation은 결국 unit의 개수를 줄이는 방법이다
따라서 이와 반대로 upsampling 효과를 주는 transposed convolution도 있다

또 자주 쓰는 테크닉으로는 1*1 convolution이라는 것이 있다
이는 커널사이즈가 1이라는 것인데
1*1 convolution은 주변 애들을 보면서 weighted sum을 해주는게 아니고
Pixel별로 움직이는 것이다
그럼 얘의 역할이 뭐냐?
채널별로 summation을 해주는 역할을 한다
각 채널별로 operation을 해주는 것이다
그럼 우리가 채널이 복수개인데 결국 output이 classification이라고 해보자
그렇다면 output에는 여러 개의 채널이 필요하지가 않다
이럴 때 보통 1*1 convolution을 이용해서 채널별로 aggregate해준다
위 1*1 convolution은 locally하게 바라보는 것이 아니다
자기 자신만 바라보는 것이다
그리고 이 과정은 여러 개의 채널을 다 계산해서 1개의 output을 뱉는 것이기 때문에
결론적으로는 fully connected network를 적용한 것과 수학적으로 동일하다

위 gpt 설명을 읽으면 이해가 더 쉬울 것 같다

그럼 이제 실제로 이 convolution neural network로
어떤 모델들을 만들고 어떤 Task를 수행하는지를 살펴보자
image classification은 imageNet이라고 하는 데이터셋이 있다고한다
각 이미지는 224*224 사이즈이고
100만개가 넘는 트레이닝 데이터가 있고 클래스도 1000개라고 한다
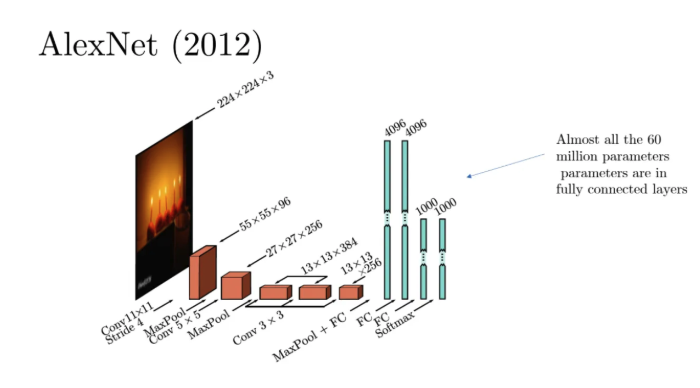
2012년에 AlexNet이라는 convolution neural network 아키텍처가 나왔다
CNN은 내가모델 커스터마이즈를 어떻게 했냐에 따라서 완전히 다른 아웃풋이 나올 수 있다고 한다
input이 컬러 이미지이기 때문에 채널은 3개이고
그 사이에 우리가 앞에서 배운 maxpooling 등등등 여러 테크닉들이 들어간다
중간에 27*26*256이 보일텐데 여기서 256이 채널 개수이다
그리고 어느시점에서 얘를 1*1로 컨볼루션해서 큰 벡터로 만들어내는데
우리는 이걸 가져와서 softmax를 수행하는 것이다
softmax를 수행하기 위해서는 실수 1개만 필요하기 때문이다
그리고 저 컨볼루션 자체의 파라미터는 몇 천개정도밖에 안되는데
FullyConnected(FC)에서만 파라미터가 가의 60 밀리언이라고 한다

이런식으로 data augmentation도 진행할 수 있다고 한다
각각 1개만 할 수 있는것도 아니고
여러가지 augmentation 기법들을 combination 할 수도 있다고 한다
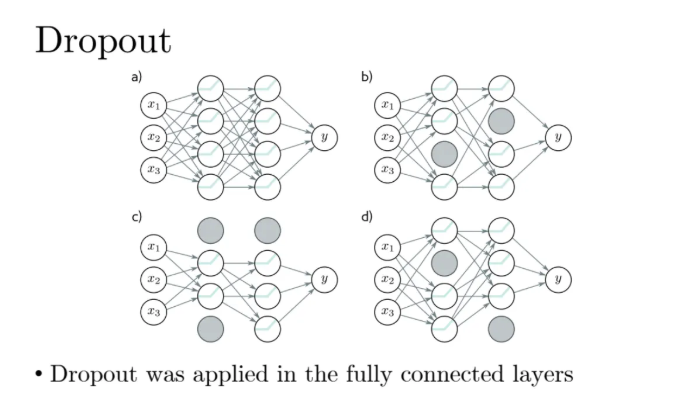
그리고 위를 train할 때 dropout도 사용했다고 한다
이건 CNN에서 말고 fully connected layer에서 사용한거다
CNN에서는 dropout과 같은 기법은 잘 사용하지 않는다

top-5-error rate이라는 것은 이미지를 줬을 때 잘 예측한 class가
top 5 class안에 들어갈지 안들어갈지이다
아무튼 그 top-5 error rate이 16.4%였다고 한다
그리고 top1개가 맞을 확률은 38%였다고 한다
이게 앞에서도 클래스가 1000개라고 했는데 이 1000개의 클래스 중에서
top5안에 든다는 것은 매우 어려운 task이다
이게 AlexNet 모델이다

두 번째로 VGGNet이라는 2010년대 중반까지 아주 널리쓰였던 네트워크를 살펴보자
original image에서 convolution으로 간 다음에 중간에 max pooling도 끼여있다
이게 점점 뭉쳐가니까 애들이 이미지 사이즈 자체는 작아지지만
flatter가 많아지기때문에 정보를 최대한 홀드하는 방향이 된다고 한다

이 VGG라는 모델은 19개의 hidden layer를 갖고있으며
144만개의 파라미터를 갖고있다
그리고 top-5-error rate이 6.8%정도라고 한다

우리가 앞에서 배운 AlexNet이랑 VGG가 처음 나왔을 때
이 모델들이 에러를 굉장히 많이 줄였다고한다
그래서 이 모델들이 한동안 아주 널리 쓰였다
그러고 나서 요즘은 트랜스포머 기반의 비전모델인 ViT, DaViT 이런것들을 주로 사용한다고한다
알렉스넷과 VGG는 사이즈가 거의 2배이상이 나온다
그런데 요즘 나오는 언어모델들은 파라미터 개수가 거의 100 빌리언 이정도도 나온다

이제 object detection을 살펴보자
이미지가 주어진 박스를 채우고 그 박스 안에 뭐가 들었는지를 찾는 task이다

object detection에는 여러 가지 방법이 있는데 그중 가장 유명한 YOLO가 있다
사실 YOLO 네트워크는 VGG와 굉장히 유사한데
얘의 아웃풋이 상당히 특이하다
아까 사용한 224 사이즈의 이미지보다는 4배가 큰 448 사이즈의 이미지를 사용해서
여기에 grid location을 주는데 이 grid는 임의로 정한 것이다
각각을 location이라고 바라보고 각각에서 predict를 수행하게 된다
거기에 그것뿐만 아니고 bounding box도 같이 predict하게 되는데
x, y coordinate와 height와 width와 confidence를 에측하는 것이다
confidence라고 하는 것은 확률값인데
그걸 각 location(grid)별로 수행한다
그렇게되면 박스들이 열심히 쳐지게 될 것이다

이렇게 위 그림처럼 박스들이 채워지게 된다
그럼 저 박스에서 각각의 예측한 것들이 존재한다
너무 의미가 없는 것들은 날려버리고 유의미한 것들만 남기는데
joint인것도 있고 intersection인것도 있다
여기서 중요한건 threshold를 넘기면 유의미하다고 판단한다는 것이다
따라서 이것도 트레이닝 데이터에서 저 박스 자체가 있어야한다
없으면 훈련을 할 수가 없다
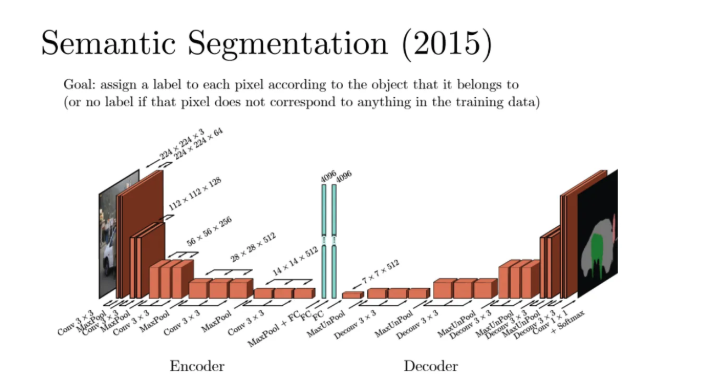
마지막으로 image segmentation을 살펴보자
segmentation은 input도 이미지이고 output도 Image이다
input이 있으면 이렇게 얘를 가지고 중간에 다양한 convolution들을 채워서 채널들도 길게 만들다가
가운데에서 FC로 정보를 쫘악 모은다
그런 다음 이걸 가지고 다시 unsampling을 수행하면서 다시 쭈우욱 간다
마지막에는 decoder가 있어서 image에 어떤게 사람이고 하는 정보들을 표시한다

따라서 image segmenation에서는 output image는 이렇게 나오게된다
이것도 supervised learning인데 y값의 매핑이 이런것이라고 충분히 매핑이 되어있어야한다
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Regularization (Dropout, Early Stopping, Transfer Learning, Data Augmentation) (1) | 2025.11.11 |
|---|---|
| [DL] Computing Gradients (Forward Pass, Back Propagation) (0) | 2025.11.10 |
| [DL] Fitting Models (0) | 2025.11.05 |
| [DL] Deep Neural Networks (0) | 2025.11.02 |
| [DL] Shallow Neural Network (0) | 2025.10.29 |