본 게시글은
서울대학교 데이터사이언스대학원 오민환 교수님의
데이터사이언스를 위한 머신러닝 및 딥러닝1 수업을
학습을 목적으로 재구성하였습니다

지난 시간에는 우리가 gradient descent, Adam 이런걸 봤고
gradient를 정확하게 어떻게 구현하는지에 대해서는 얘기를 안했다
지난 시간에 얘기했던 gradient는 정확하게 어떻게 계산되는건지에 대해서 이번 시간에 배워보고
사실 neural network에 대한 업데이트를 하려면
각각의 레이어에 대해서 gradient를 구해야하는데 이를 어떻게 하는지 살펴본다

우리가 앞에서 봤던 loss function이다
loss function은 데이터, 모델, 파라미터를 기준으로 구한다고 했다

위는 hidden layer가 3개가 있는 neural network이다
input도 dimension이 3, output도 dimension이 2이다
여기서 중요한 것은 hidden layer가 3개라는 점이다
각각의 input에서 preactivation까지 오는 저 activation이 한 개의 h1
h1의 hidden unit에서 받아서 h2의 input으로 들어간다

loss 함수와 총 데이터의 개수 I개가 있다
그리고 SGD에서는 각각의 데이터포인트에 대해서 gradient가 있다
그럼 파라미터들은
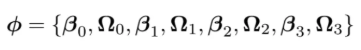
위와 같이 존재하게 된다
전체를 퉁쳐서 파라미터에 대한 gradient라고 하는데
우리가 네트워크를 업데이트한다는 것은 phi들을 업데이트하는 것이다
즉, 각각의 레이어에서 bias vector인 B와
weight matrix인 오메가를 업데이트 하겠다는 것이다
데이터 포인트를 우리가 각각의 k번째 weight와 matrix와
각각의 k번째 bias vector에 대해서 미분하는 것이다
이 과정에서 총 I개의 데이터 포인트에 대해서 hidden layer가 k-2개가 있다면
그럼 순수 SGD의 경우 총 몇 번의 gradient update가 일어나는것인지
감이 잘 안와서 gpt와 열심히 대화를 주고받았다
결론은 이렇다
데이터포인트의 개수가 총 1000개
hidden layer의 개수가 100개가 있다고 치면
우리가 이전에 배운 full batch gradient descent의 경우
전체 데이터포인트 1000개에 대해서 loss를 계산한다
뭐 각 데이터포인트의 loss를 구한다음 이를 평균내거나 할 것이다
그런 다음 우리가 앞으로 배울
forward 1회, backward 1회, parameter update 1회를 수행한다
이게 1 epoch이 되는 것이고 한 마디로 full batch gradient descent는
1 epoch에 대해서 총 파라미터 update를 1회만 수행하는 것이다
그럼 pure SGD로 한 번 살펴보자
우리가 앞에서 pure SGD는 데이터포인트 1개에 대해서 loss를 계산한다고했다
그럼 데이터포인트가 1000개가 있으면
총 1000개의 데이터포인트에 대해서 loss를 각각 계산하고
각 데이터포인트에 대한 loss에서 forward, backward, parameter update를 1번씩 수행해서
1 epoch에 대해서 총 1000번의 parameter update를 수행하게 되는 것이다

위 내용을 읽으면 좀 더 이해가 쉬울 것이다
그리고 k번째의 phi set이 있다는 뜻은
hidden layer는 총 k-2개가 있다는 뜻이 된다
input layer와 output layer를 제외해서 hidden layer는 k-2개가 된다
아래 설명을 읽으면 더 이해가 쉽다


그렇다면 우리가 위 과정이 왜 이렇게 힘든지 보자
아무튼 neural network를 식으로 쓰면 위처럼 생겼다고 한다
그런데 이게 우리가 아까 위에서 설명했던 것처럼
gradient를 계산하기 위해서는 각각의 파라미터 기준으로
다 loss에 대한 미분값을 구해야 한다
예를 들어서 SGD라고 한다면 아까 위에서
1000번을 update하는데
각 phi set에 베타가 0부터 3까지, 오메가가 0부터 3까지 있다고하자
그럼 총 8개의 파라미터에 대해서 각각 편미분을 해줘야하는 것이다
그런데 더 문제는?
이 베타도, 오메가도 또 벡터값이라는 것이다
베타와 오메가가 있는 k번쨰 layer의 hidden unit 개수에 따라서
각 베타와 오메가의 차원이 정해지고
이걸 이용해서 또 각각 미분을 해주려고 하면 실제로는 수백만개의 파라미터에 대해서 미분을 해줘야하는 것이다
그래서 사실상 거의 현실적으로 불가능하다고 할 수 있다

그렇다면 두 번째 문제는 무엇이냐
이전 시간에 배웠던 내용인데 initial 지점에 따라서
내가 도달하고자하는 지점이 달라질 수 있다는 것이다
SGD로 하면 local minimum에 덜 빠질 수는 있지만
이것도 절대 빠지지 않는다는 보장은 없다

따라서 위의 두 가지 문제를 해결할 수 있게 해주는 것이
바로 1986년에 back propagation이라고 한다

이 back propagation의 원리는 미적분에서 나온 chainrule의 원리이다
원래는 합성함수의 미분값을 구할 때 쓰는게 chain rule인데 이를 적용시킨다
위 ppt slide처럼 네트워크가 이렇게 있을 때
여전히 hidden layer는 3개이다
저 input이 들어와서 첫 번째 레이어를 통과해서 나오는
저 오메가 1쪽의 선을 한 번 보자
이 unit이 그냥 linear로 매핑이 된 다음
activation을 타고 이렇게 가는 것이다
여기서 곱해주는 친구는 preactivation된게 activation을 지나서
어떤 상수배가 된 이후에 다음 레이어로 들어가게 되는 것이다
그럼 여기서 우리가 관심있는게 뭐냐?
쟤가 얼만큼 바뀌었을 때 저 끝에 있는 output에 얼만큼 영향을 미치냐이다
여기에 대한 미분값을 구한다는 것은
여기서 뭘 조금 바꿨을 때 loss값이 얼만큼 변하는지가 궁금한 것이다
저기서 뿐만이 아니고 모든 connection에서 궁금한 것이다

위 부분에서도 마찬가지다
저 빨간 화살표에서 어떻게 하냐에 따라서 저 뒤에 친구들에게도 영향을 미친다
그 weight와 bias들의 작은 변화가
어떻게하면 h3을 바꾸는지
혹은 h3가 얼마나 loss를 변화시키는지를 알고 싶은 것이다
h3에 있는 저 레이어의 변화가 모델 아웃풋을 바꿀 것이고
그 모델 아웃풋을 바꾸면 loss가 달라지게된다
근데 그건 뒤에서뿐만이 아니고 다른 곳에서도 마찬가지이다
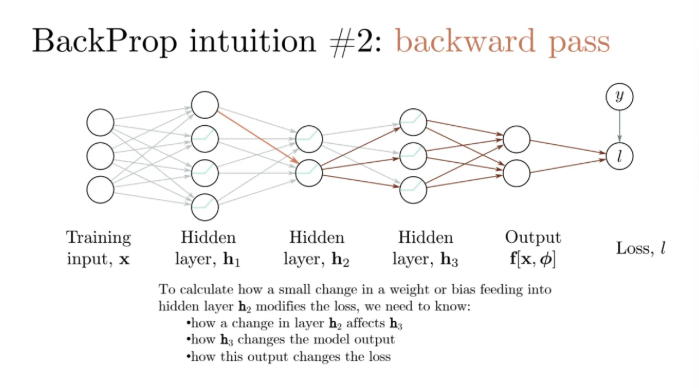
이걸 앞에서 바꾸면 뒤에서 더 영향을 많이 미치게 될 것이다

즉 레이어 한 개를 바꾸는데에 있어서 나머지 레이어들에게도 영향을 미친다는 뜻이다
그리고 그게 최종적으로는 output에 영향을 미친다
그렇다면 위 toy model을 한 번 보자
이건 Neural network는 아니고 그냥 합성함수이다
input과 output이 모두 1차원이라고 해보자
여기서 파라미터는 오메가, 베타들이 있을 것이다
그리고 Loss에 대해서는 내가 squared error로 설정한다고 해보자
그리고 위 식에서 activation 역할을 하는 것은 cos, sin인데
이게 neural network랑 같은 것은 아니다

위는 삼각함수에서 배운 미분값들이다
cos 함수를 미분하면 -sin함수가
sin함수를 미분하면 cos함수가 된다

그렇다면 아까도 우리가 말했지만
우리가 관심있는건 각각의 파라미터들을 살짝 변화시켰을 때
loss가 이로 인해 얼만큼 변하는지이다
위의 예시에서 파라미로토 베타가 0부터 3까지 오메가가 0부터 3까지 있다
로스의 미분값은 각각의 파라미터에 대한 것이라고 했다
파라미터는 총 4쌍씩 8개가 있다

이걸 미분값을 가져와서 구하면 이렇게 나온다
이게 오메가 0에 대해서 한 개를 구한거다
이 식이 이렇게 복잡한 이유는 가장 안쪽에 있는 파라미터이기 때문이다

근데 이걸 위와 같은 방식으로 하지말고 식을 쪼개서 생각해보자
가장 위의 f0은 sin안에 들어있는 linear 함수이다
h1은 그냥 저 sin함수 자체이다
각각의 operation을 이렇게 모듈러로 바라보자

이 각각의 operation을 이렇게 모듈러로 바라보면
이 함수를 계산하는 순서는 위 그래프처럼 표현할 수 있다

그럼 이걸 우리가 아까 위에서 했던 것처럼
베타나 오메가같은 파라미터 기준으로 편미분하는게 아니고
모듈러함수를 기준으로 미분해보자는 것이다
각각의 모듈러 함수를 기준으로 위처럼
f0부터 f3까지, h1부터 h3까지 미분해보자

그럼 그 모듈러 함수를 기준으로 미분을 적용하면
chain rule이 적용돼서 함수의 operation 순서가 바뀌게 된다

그렇다면 제일 끝의 친구부터 한 번 살펴보자
loss를 f3을 기준으로 미분을 하게 되면 위와 같은 결과가 나오게 된다

그럼 이제 그 다음 순서인 h3를 한 번 살펴보자
h3을 기준으로 loss를 미분하게 되면 loss에서 f3을 기준으로 미분한 것에서
f3을 h3을 기준으로 미분 한 것을 곱해줘야한다
그럼 이게 총 loss에 대해서 h3이 변하는게
어느정도로 영향을 미치는지를 알 수 있는 식이 되는 것이다
이게 chain rule의 법칙이다

그런데 우리가 뒤에 f3의 미분값은 이미 구했다

바로 윗 값이었다
그럼 f3을 h3에 대해서 미분하면 뭐만 남게 되냐?
w3만 남게되는 것을 확인할 수 있다

그렇다면 이제 그 다음 순서로 가서
loss에 대해 f2로 미분한 식을 구하고 싶다
그럼 지금까지 구했던 h3에 대한 미분식에서
다시 h3을 h2에 대해서 미분한 식을 곱해주면 된다
그럼 앞의 h3에 대한 미분식은 이전에 이미 구했고
h3을 f2에 대해서 미분한 식은 -sin[f2]가 된다
이런식으로 계속해서 미분을 진행할 수 있게 된다

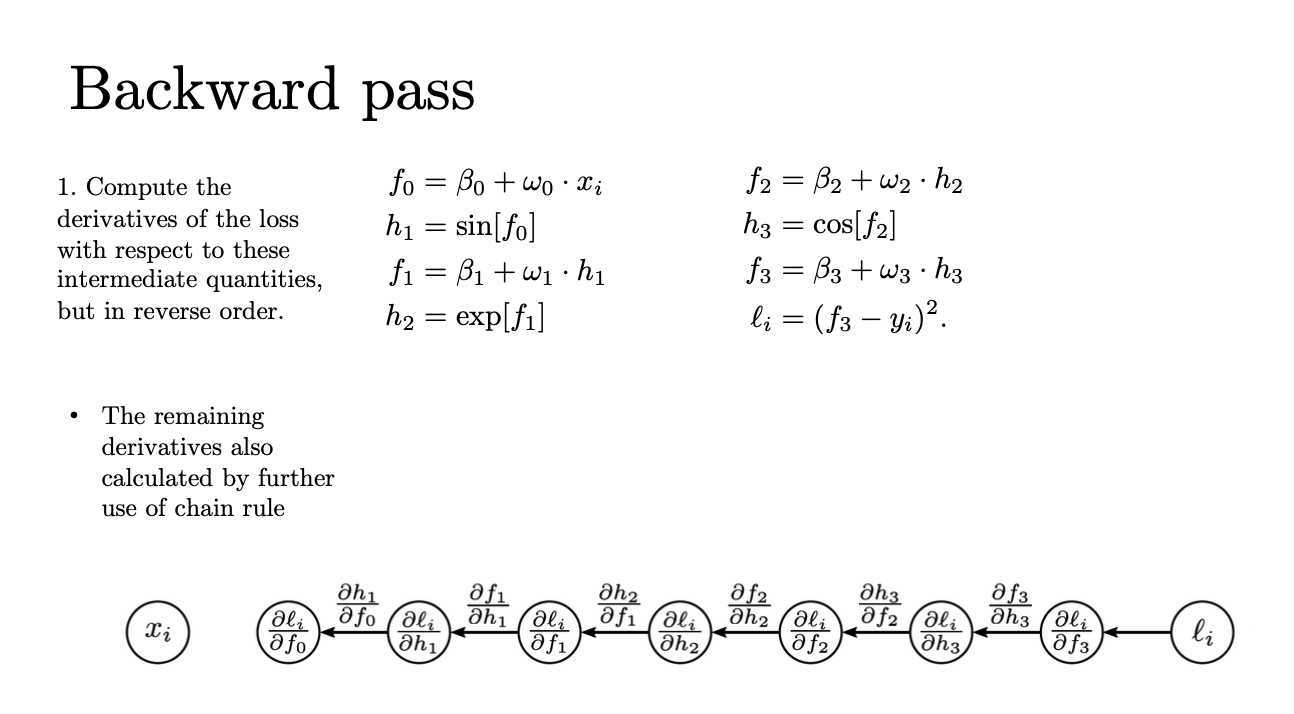
이렇게 우리가 지금까지 봤던 함수를 가장 처음인 f0까지 계속해서 미분할 수 있다
그래서 각 모듈러들을 타고 미분값들의 곱으로 구할 수 있다
f0이 궁금하면 뒤에서부터 쫘악 계산하기 때문에 이게 미분들의 곱으로 이루어지는데
각각의 항들이 단순한 operation이기 때문에 쟤네들을 곱하기만 하면 된다는 것이다

그럼 우리가 이렇게 각각의 모듈러들에 대해서 알아봤는데
사실 우리가 궁금한 건 f나 h와 같은 모듈러 함수들에 대한 미분값이 아니다
파라미터인 베타나 오메가들에 대한 미분값이다
그럼 이제 그걸 어떻게 하는지 살펴보자

loss에서 특정 오메가 k를 기준으로 미분하고싶다
만약에 k=1라고 한다면
f1까지 끌고 온 다음에 f1을 오메가1에 대한 미분값으로 끌고오면 된다
위에서 f1을 오메가1로 미분하면 그냥 h1만 남게된다
k=2라고 한다면 f2를 오메가2로 미분하는 것이고 그냥 h2만 남ㄴ게된다
그래서 이 값은 일반화해서 그냥 hk가 되는 것이다
그리고 뒤의 loss를 fk를 기준으로 미분하는 것은 우리가 이미 앞에서 계산했다

그렇다면 베타에 대해서도 마찬가지이다
베타k에 대한 미분값을 구하려고 한다면

위와 같이 미분곱으로 나타내줄 수 있다
이렇게 되면 fk에 대해서 베타k를 기준으로 미분하면
미분값은 그냥 1이 된다
뒤의 식은 앞에서 이미 구했으니 알 수 있다

그렇다면 위식에서 우리가 각 오메가 베타에 대한 파라미터값들로
미분하려면 위와 같이 그림으로 표현할 수 있다
각각의 step별로 내가 원하는 오메가 또는 베타의 미분값을 구할 수 있는 것이다
어느 layer에서의 어느 weight vector, bias vector건 내가 구할 수가 있는 것이다
이런걸 우리가 back propagation이라고 하는데
이게 미분값들의 propagation이라는 뜻이다
이걸 loss에서 끌고와서 쭈욱 가져와서 내가 원하는 layer의 파라미터의 weight, bias vector 기준으로
미분값들을 언제든 구할 수가 있는 것이다
그리고 이게 다 chain rule이다

우리가 위의 예시에서는 scalar를 기준으로 봤는데
사실 neural network에서는 bias는 벡터 weight는 matrix가 된다
그런데 이걸 어떻게 미분을 하느냐?
벡터에 대한 미분은 각각의 element에 대해 partial하게 미분하면 된다
위의 예시처럼 element-wise하게 수행하면 되는 것이다
matrix도 마찬가지

그렇다면 matrix를 한 번 살펴보자
각각의 a란 벡터에 대해서 미분을 구한다라고 하면
각각의 element에 대해서 미분을 하는 것이니까
4*3 matrix가 된다

scalar에서와 matrix에서의 계산을 비교해보자
위 경우 scalar에서는 f를 h에 대해서 미분하면 그냥 오메가가 나오는데
아래 벡터 연산은 저렇게 나오게 된다

이것도 똑같은데 scalar에서는 그냥 미분하면 1이 나오는데
아래 벡터의 경우는 1이 아니고 단위행렬 I가 나오게 된다

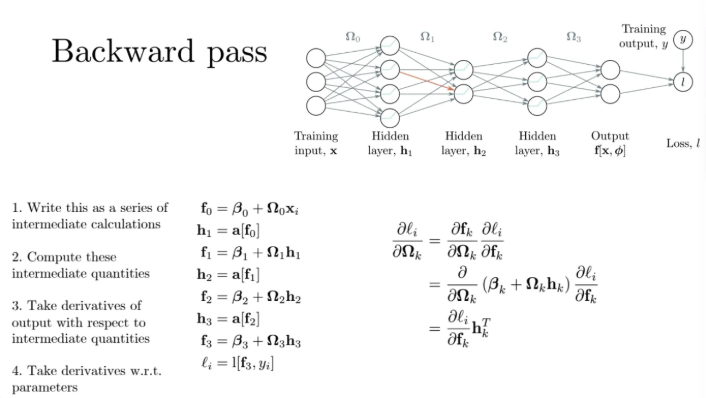
그렇다면 이제 실제 neural network를 바탕으로 forward, backward pass를 살펴보자
앞에서 봤던 모듈러 함수들을 위와 같이 정의해준다
f0은 저 위 neural network에서 h1으로 들어가기 전까지의 값이다
f0을 activation한게 첫 번째 hidden layer가 된다
그래서 h1은 위와 같이 정의되는 것이다
여기 나오는 오메가와 벡터값들은 전부 벡터값이다
그렇다면 여기서는 지금 몇 dimension이 되냐?
unit이 4개이기 때문에 4 dimension이 된다
그래서 이 h1의 값을 두번째 layer에 들어가기직전까지 저 화살표의 값이 f1이 된다
그런 다음 이 h1을 activation시킨게 h2 layer에 들어간 값이 되고
따라서 h2=a[f1] 이렇게 쓸 수 있는 것이다
이건 그냥 forward pass의 과정이다
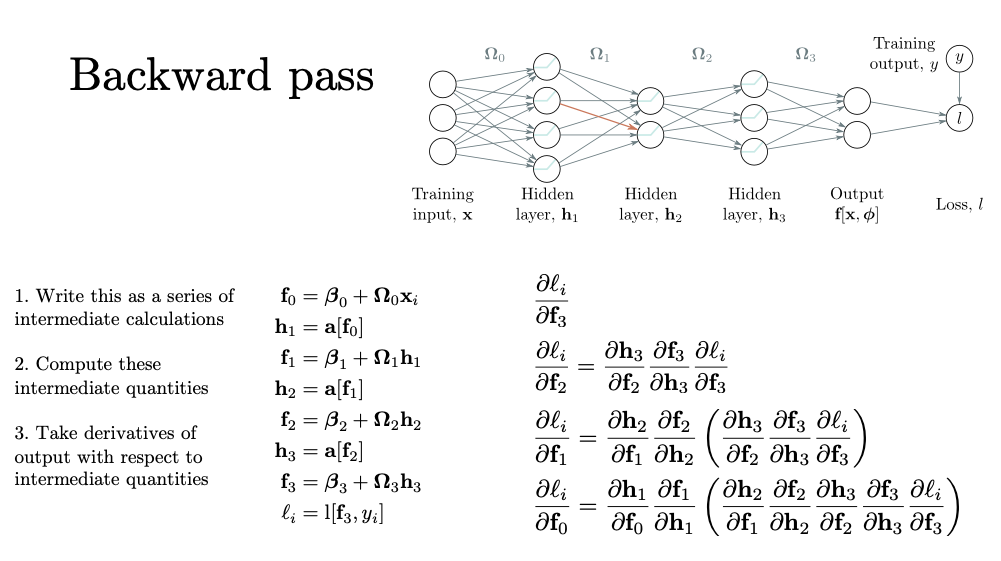
그럼 여기서 우리가 backward pass를 하고싶다고 생각해보자
그럼 이걸 위해서 preactiviation과 activation을 타고 하는
hidden unit별로 미분값을 먼저 구한다
그렇게 되면 preactivation 기준으로 f3에 대한 미분값을 가장 먼저 구할 수 있고
이건 loss function에 대해서 바로 구할 수 있다
그럼 이제 우리가 loss에 대해서 f2를 기준으로 미분한 값을 구하고 싶다고 하자
그럼 이건 f3과 h3과 연관이 되어 있으므로

위와 같이 구할 수 있다
가장 뒤에건 우리가 이미 앞에서 계산했고
가운데의 f3을 h3에 대해서 미분한 값은 그냥 오메가가 된다
그렇게 되면 이제 h3 함수를 f2에 대해서 미분한 값만 구하면 쉽게 계산이 된다
f1에 대해 미분한 것도 잘 살펴보자

위 식인데 여기서 괄호를 친 부분은 앞에 계산했던 것과 동일하다
그래서 이전 레이어에서 구해놨던 것을 재사용하면 되고
이제 앞의 두 미분값만 구해서 곱해주면 된다
f0에 대해서도 마찬가지이다
괄호친 것은 이전에 구해놓은 것이라 새로 구할 필요가 없다

그렇다면 위의 노란박스 친 부분을 한 번 살펴보자
아까 쟤의 값이 오메가3이었던 것을 알 수 있다

그럼 이 오메가는 matrix이기 때문에 계산하면 위처럼 된다는 것을 알 수 있다

그렇다면 이제 우리가 아까 구하고자했던
위 노라나 박스를 살펴보자
위 노란박스는 activation 함수를 넣은 값에 대한 미분값이다

ReLU 함수를 기준으로 activation 함수는 위와 같다
그럼 이건 0 이하에서는 미분값이 0이고
0보다 클 때는 그냥 그 1이 미분값이 되는 것을 알 수 있다

한 마디로 이 친구들을 각각의 ReLU 값으로 미분을 해주면 되는데
각각의 preactivation 값이 0보다 크면 이 친구들이 1이고 작으면 0이 된다
여기서 우리는 각각의 a1, a2, a3에 대한 ReLU 미분값을 구할건데

위와 같이 나타낼 수 있다
그런데 여기서 a2는 b1과 아무런 관련이 없다
따라서 첫번째 행의 2, 3번째 column은 각각 0이 되고
두번째 행도 마찬가지이다
a2와 b2만이 관련이 있기 때문에 가운데만 살아남고 나머지는 0이 된다
마지막 행도 마찬가지
따라서 이 행렬식은 결국 대각행렬이 되고 그렇기 때문에 결국
ReLU 기준 activation 함수의 미분값은
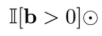
위 0 혹은 1의 스위치값을 곱해주는 것과 동일해진다

그걸 위와 같은 identity matrix를 써서 표현을 했다
여기서는 activation된 부분만 1로 되는 것이다
element-wise로 activate된 것은 1이고, 그렇지 않은 것은 0이 되는 diagonal matrix가 된다
그래서

결국 우리가 아는 각 항들의 미분값들과
diagonal matrix를 곱해주면
loss 함수를 f2에 대해서 미분한값을 구할 수 있게 된다
그렇다면 이렇게만 하면 끝나나?
아니다
우리가 아까도 toy model로 수행했을 때도
사실상 우리가 정말 원하는 것은 오메가, 베타와 같은 파라미터에 대한 미분값이었다

오메가와 베타에 대한 미분값을 구하기 위해서 위처럼 수행해주면된다
이 베타k에 대한 미분값을 구하려면

위와 같이 진행하면 되는데
fk를 bk에 대해서 미분하면 identity matrix만 남게 된다
그래서 결국 뒤의 항인
loss function을 fk에 대해 미분한 값만 남게 되는 것이다
그럼 오메가인 weight matrix에 대한 미분값은?
오메가k에 대해서 미분값을 구하기 위해서는

위와 같이 미분곱으로 나타낼 수 있는데
이 fk를 오메가k에 대해서 미분하면
hk만 남게 된다
그럼 이 hk와 뒤의 loss function을 fk로 미분한 값을 곱해주면 된다

그럼 위와 같은 식이 최종적으로 나오게 된다
이게 바로 전반적인 back propagation의 과정이다
하나하나를 모듈러 함수로 끊은 다음
내가 미분가능하게 만들면 되는 것이다
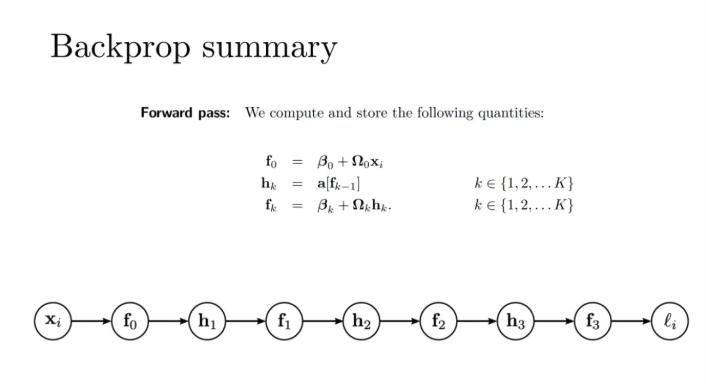
지금까지 배운 back propagation을 한 번 요약해보자
우선 forward를 수행해서 각각의 layer별로 input을 받는다
걔네가 fk 함수가 된다
그러고 이 fk를 activation시킨게 hk함수가 된다
이렇게 forward pass의 과정이 수행이 된다

그렇다면 이걸 back propagation으로 가져온다는 말은
위에서도 설명했듯이 이걸 각각의 f에 대해서 미분을 수행한 다음
이걸 이용해서 오메가, 베타들까지 끌고와서 미분을 수행해주면 되는 것이다
bk의 미분값은 그냥 fk에 대한 미분값 그대로 가져오면 됐었고
오메가k에 대한 미분값은 fk에 대한 미분값에다가 hk의 transpose만 곱해주면 됐었다
이렇게 내가 원하는 레이어에서 파라미터의 미분 값을 다 구할 수가 있다
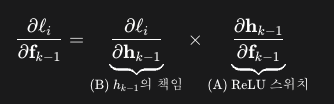
k 레이어 기준 이전 레이어인 k-1에서로 이를 넘겨주기위해서는
위의 값을 계산해야하는데
이 과정이 아래와 같이 정리되어서

최종적으로 아래와 같이 나타낼 수 있다고 한다


이런 back propagation의 장단점을 알아보자
hidden layer의 개수가 많건 적건
모듈러 단위로 구할 수 있다
back propagation을 쓰지 않았을 때는 미분값 구하기가 상당히 복잦ㅂ했는데
그거에 대해 back propagation을 수행하면
그냥 모듈러 단위로 계산하는 것이 되기 때문에
계산하기가 아주 용이하고 이전에 미리 계산해 놓은 것들을 다시 사용할 수도 있다
단점이라고 한다면 이걸 계산하기 위해서는 예전에 계산하고 있었던 것을
모두 hold를 하고 있어야한다
이 계산량을 줄이기 위해서 모듈러를 하려면 이전에 계산한 미분값을 재사용해야한다
즉, 중간중간 값들을 가지고 있어야한다는 뜻이다
그래서 gpu memory는 즉 이 gradient들을 hold하고 있어야하는 메모리이고
이건 보면 알겠지만 굉장히 sequential하게 이루어진다
이걸 하면 다름 레이어들에 대한 미분값을 가져오면서 서로 영향을 미치기 때문이다
따라서 batch별로는 parallel하게 연산을 수행할 수는 있어도
이를 layer별로 parallel하게 연산하는것은 힘들다

위 back propagtaion의 모든 과정을 이전에는 다 하드코딩을 수행했다고 한다
레이어별로 어떻게 짰는지 코드를 짠 다음에 다 define 했었어야 했는데
요즘은 이런걸 pytorch 이런데서 다 지원해주고 있다
이런걸 auto differentiation이라고 한다고 한다..
'강의 > machine learning & deep learning' 카테고리의 다른 글
| [DL] Convolutional Neural Networks (CNN) (0) | 2025.11.17 |
|---|---|
| [DL] Regularization (Dropout, Early Stopping, Transfer Learning, Data Augmentation) (1) | 2025.11.11 |
| [DL] Fitting Models (0) | 2025.11.05 |
| [DL] Deep Neural Networks (0) | 2025.11.02 |
| [DL] Shallow Neural Network (0) | 2025.10.29 |